＜数据结构＞刷题笔记——链表篇（二）（有动图详解）

目前在不断更新<数据结构>的知识总结
该系列相关文章：
＜数据结构＞还不会写单向链表？我手把手教你
＜数据结构＞刷题笔记——链表篇（一）
已完结系列：
c语言自学教程——博文总结
我的gitee：gitee网址
期待系统学习编程的小伙伴可以关注我，不迷路！

从现在开始，我们要引进快慢指针的概念，它在做一些链表题目时非常方便。

1. 链表的中间结点

给定一个头结点为 head 的非空单链表，返回链表的中间结点。
如果有两个中间结点，则返回第二个中间结点。

示例 1：
输入：[1,2,3,4,5]
输出：此列表中的结点 3 (序列化形式：[3,4,5])
返回的结点值为 3 。 (测评系统对该结点序列化表述是 [3,4,5])。
注意，我们返回了一个 ListNode 类型的对象 ans，这样：ans.val = 3, ans.next.val = 4, ans.next.next.val = 5, 以及 ans.next.next.next = NULL.

示例 2：
输入：[1,2,3,4,5,6]
输出：此列表中的结点 4 (序列化形式：[4,5,6])
由于该列表有两个中间结点，值分别为 3 和 4，我们返回第二个结点。

提示：
给定链表的结点数介于 1 和 100 之间。

解题思路：

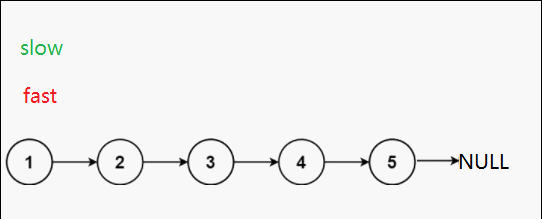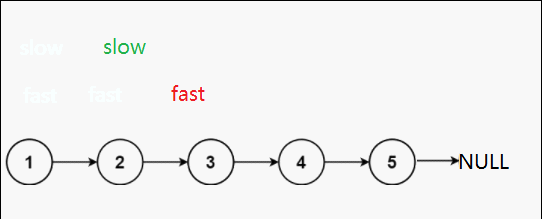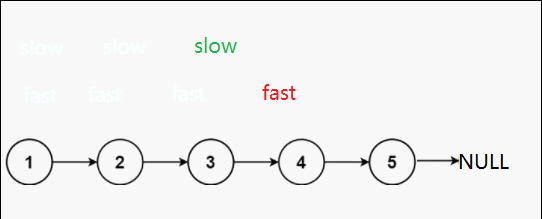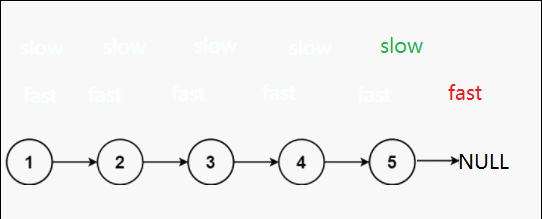
慢指针一次走一步，快指针一次走两步，这样的话当快指针走到终点时，慢指针刚好走到中间节点处。
第一种可能：单数个节点

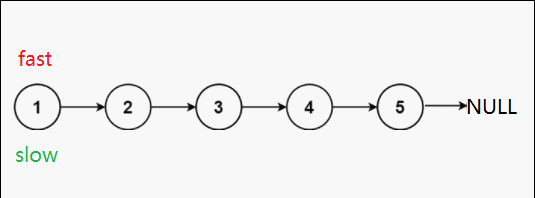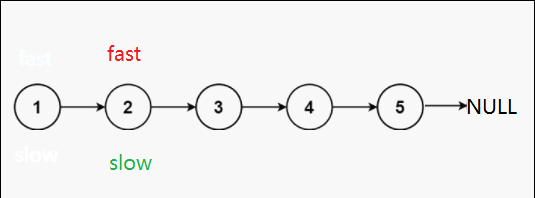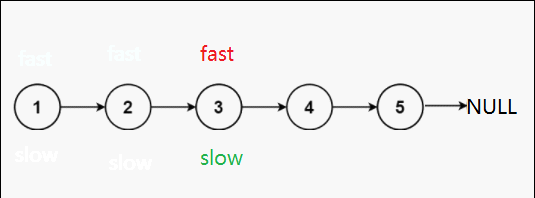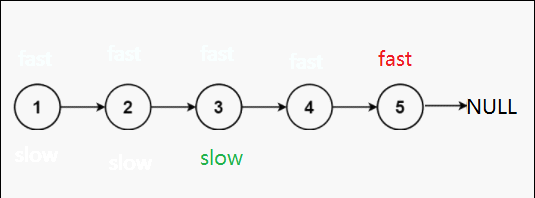
第二种可能：双数个节点

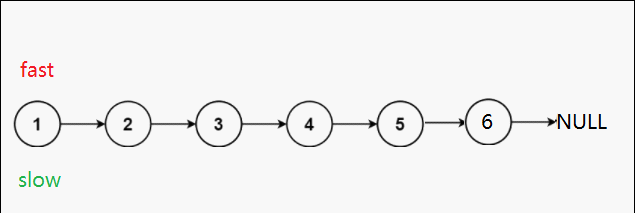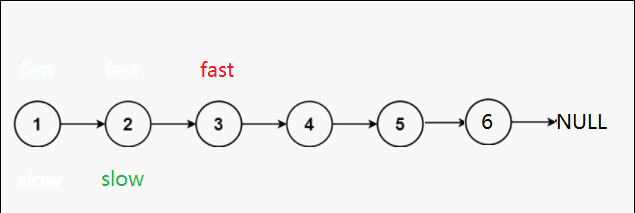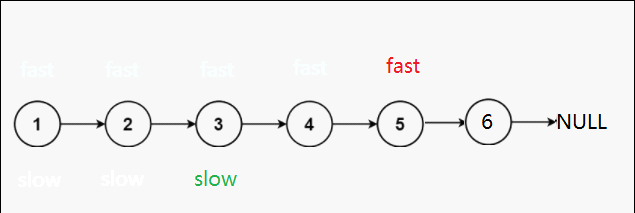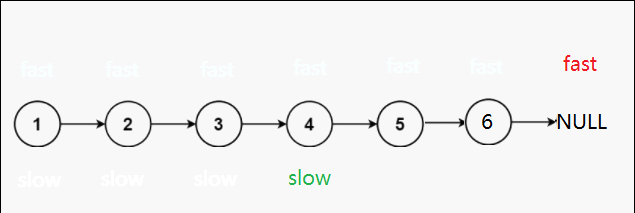
struct ListNode* middleNode(struct ListNode* head){
    struct ListNode* fast,*slow;
    fast = slow = head;
    while(fast && fast->next)
    {
        slow = slow->next;
        fast = fast->next->next;
    }
    return slow;
}

链接：

力扣876. 链表的中间结点

2. 链表中倒数第k个结点

输入一个链表，输出该链表中倒数第k个结点。

示例
输入： 1,{1,2,3,4,5}
返回值：{5}

解题思路：

让我们换一个角度看这道题，倒数第k个结点也可以看做正数第n-k个节点（n是链表的节点总数）。
这种思路就可以借助快慢指针轻松解决问题了。
首先让快指针走k步，之后让慢指针从起点开始走，快慢指针一起走，快指针走到终点时慢指针走到的地方就是链表中倒数第k个结点了。是不是很巧妙呀。
但要注意检查k的大小。

struct ListNode* FindKthToTail(struct ListNode* pListHead, int k ) {
    // write code here
    struct ListNode* fast,*slow;
    fast = slow = pListHead;
    
    while(k--)
    {
        if(fast ==NULL)//小心k过大
            return NULL;
        fast = fast->next;
    }
    
    while(fast)
    {
     	fast = fast->next;
        slow = slow->next;
    }
    return slow;
}

链接：

牛客：链表中倒数第k个结点

3. 链表的回文结构

描述：
对于一个链表，请设计一个时间复杂度为O(n),额外空间复杂度为O(1)的算法，判断其是否为回文结构。
给定一个链表的头指针A，请返回一个bool值，代表其是否为回文结构。保证链表长度小于等于900。

测试样例：
1->2->2->1
返回：true

解题思路：

回文通俗点讲就是，从前往后读和从后往前读是一样的。
这道题有一个取巧的办法，题目中有讲“保证链表长度小于等于900”，由此想到能开一个数组把链表里的数据按顺序放到数组里，再判断数组元素是否是回文。但不建议使用这种解法，因为如果没有告诉链表最大长度，则不能用此解法。

class PalindromeList {
public:
    bool chkPalindrome(ListNode* A) {
        // write code here
        int a[900] = {0};
        ListNode* cur = A;
        int n = 0;
        //保存链表元素
        while(cur)
        {
            a[n++] = cur->val;
            cur = cur->next;
        }
        //判断数组是否为回文结构
        int begin = 0, end = n-1;
        while(begin < end)
        {
            if(a[begin] != a[end])
                return false;
            ++begin;
            --end;
        }
         
        return true;
    }
};

还有一种更巧妙的，灵活性更强解法：将后半段链表反转，如果链表是回文结构，反转后的和前半段的数据是一一对应的。

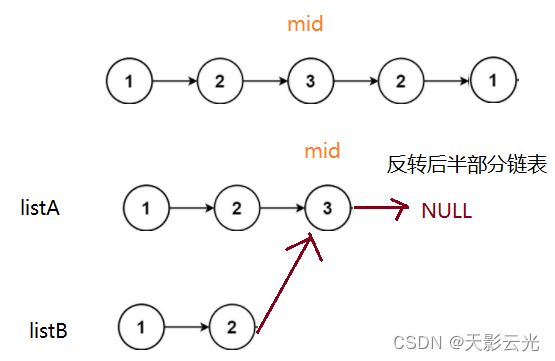
你肯定在想要不要分情况讨论，但这种方法巧就巧在这里，以上图为例，1和2比较到时候没有任何问题，listA和listB的下一个节点是同一个3，那肯定一样啦。之后再一起走向NULL，循环终止。
这就是要讲的相交链表的雏形，很快就讲相交链表咯
程序我就直接用了之前写的找中点和反转的函数。

class PalindromeList {
 struct ListNode* reverseList(struct ListNode* head)
 {
     struct ListNode* newhead = NULL, *cur = head, *next;
     while(cur)
     {
         next = cur->next;
         cur->next = newhead;
         newhead = cur;
         cur = next;
     }
     return newhead;
 }
 struct ListNode* middleNode(struct ListNode* head)
{
    struct ListNode* fast,*slow;
    fast = slow = head;
    while(fast && fast->next)
    {
        slow = slow->next;
        fast = fast->next->next;
    }
    return slow;
}
public:
    bool chkPalindrome(ListNode* A) {
        // write code here
        struct ListNode *mid = middleNode(A);
        struct ListNode *listB = reverseList(mid);
        while(A&&listB)
        {
            if(A->val == listB->val)
            {
                A = A->next;
                listB = listB->next;
            }
            else return false;
        }
        return true;
    }
};

链接：

牛客OR36 链表的回文结构

在讲下一题之前我们要复习一下带头节点单链表和无头单链表的区别。顾名思义，带头结点的单链表有一个哨兵卫的头结点，但这个节点不存储有效数据。那么它有什么意义吗？它能够简化过程，让第一次插入和非第一次插入合并起来，详情请见上一篇＜数据结构＞刷题笔记——链表篇（一）。下面这题我们就用这个结构。

4. 链表分割

现有一链表的头指针 ListNode* pHead，给一定值x，编写一段代码将所有小于x的结点排在其余结点之前，且不能改变原来的数据顺序，返回重新排列后的链表的头指针。

解题思路：

题目描述就到此为止了，惊不惊喜意不意外。但别担心，我会尽力跟你们讲明白的。

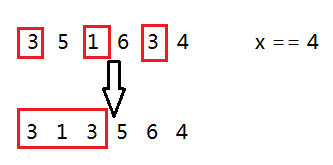
就像这张图，比4小的数放到前面，并且相对位置不变，大于等于4的放到后面，相对位置也不变。
在原链表上捣鼓实在太混乱了，我就想到新开2个链表，一个放比x小的，另一个放大于等于x的，最后再将两个链表连接起来（新链表最好是带头的，不然会很窒息，太复杂了）

还有一个很重要的细节，如果是下图的情况，6到3的指向关系没有被改变，它跟新创建的指向关系共同形成了一个环，使程序死循环。对此我们让6指向NULL就能解决问题。

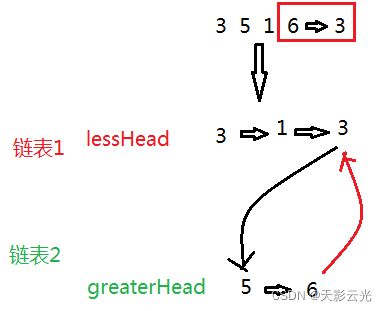
水可载舟亦可覆舟，上一题借助保留的指向关系快速解题，这一题隐藏的指向关系成了陷阱，我们还是得认真分析，仔细思考，养成严谨的习惯，题做多了就有感觉了，不要着急。

class Partition {
public:
    ListNode* partition(ListNode* pHead, int x) {
        // write code here
        ListNode* lessHead,*lessTail, *greaterHead, *greaterTail;
        lessHead = lessTail = (ListNode*)malloc(sizeof(ListNode));
        greaterHead = greaterTail = (ListNode*)malloc(sizeof(ListNode));
        
        lessTail->next = greaterTail->next = NULL;
        ListNode* cur = pHead;
        while(cur)
        {
            if(cur->val < x)
            {
                lessTail->next = cur;
                lessTail = lessTail->next;
            }
            else
            {
                greaterTail->next = cur;
                greaterTail = greaterTail->next;
            }
            cur = cur->next;
        }
        
        lessTail->next = greaterHead->next;
        greaterTail->next = NULL;//使尾端指向NULL，防止形成环
        
        ListNode* list = lessHead->next;
        free(lessHead);
        free(greaterHead);
        return list;
    }
};

链接：

牛客CM11 链表分割

5. 相交链表

给你两个单链表的头节点 headA 和 headB ，请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点，返回 null 。

图示两个链表在节点 c1 开始相交：

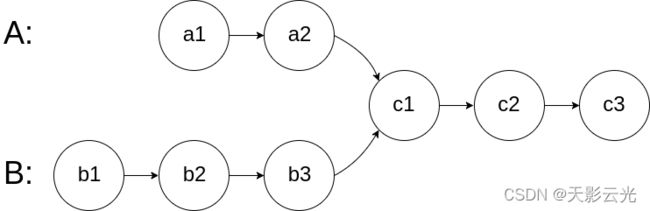
题目数据 保证 整个链式结构中不存在环。
注意，函数返回结果后，链表必须 保持其原始结构 。

自定义评测：
评测系统 的输入如下（你设计的程序 不适用 此输入）：
intersectVal - 相交的起始节点的值。如果不存在相交节点，这一值为 0
listA - 第一个链表
listB - 第二个链表
skipA - 在 listA 中（从头节点开始）跳到交叉节点的节点数
skipB - 在 listB 中（从头节点开始）跳到交叉节点的节点数
评测系统将根据这些输入创建链式数据结构，并将两个头节点 headA 和 headB 传递给你的程序。如果程序能够正确返回相交节点，那么你的解决方案将被 视作正确答案 。

示例 1：

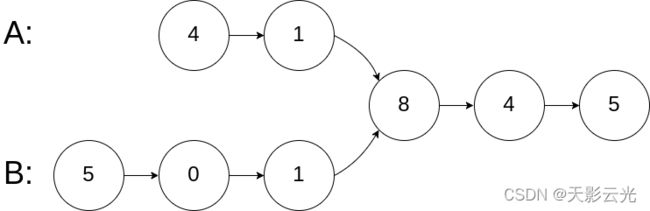
输入：intersectVal = 8, listA = [4,1,8,4,5], listB = [5,6,1,8,4,5], skipA = 2, skipB = 3
输出：Intersected at ‘8’
解释：相交节点的值为 8 （注意，如果两个链表相交则不能为 0）。
从各自的表头开始算起，链表 A 为 [4,1,8,4,5]，链表 B 为 [5,6,1,8,4,5]。
在 A 中，相交节点前有 2 个节点；在 B 中，相交节点前有 3 个节点。

示例 2：

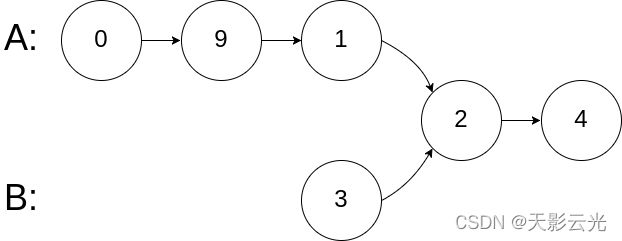
输入：intersectVal = 2, listA = [1,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1
输出：Intersected at ‘2’
解释：相交节点的值为 2 （注意，如果两个链表相交则不能为 0）。
从各自的表头开始算起，链表 A 为 [1,9,1,2,4]，链表 B 为 [3,2,4]。
在 A 中，相交节点前有 3 个节点；在 B 中，相交节点前有 1 个节点。

示例 3：
输入：intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2
输出：null
解释：从各自的表头开始算起，链表 A 为 [2,6,4]，链表 B 为 [1,5]。
由于这两个链表不相交，所以 intersectVal 必须为 0，而 skipA 和 skipB 可以是任意值。
这两个链表不相交，因此返回 null 。

提示：
listA 中节点数目为 m
listB 中节点数目为 n
1 <= m, n <= 3 * 104
1 <= Node.val <= 105
0 <= skipA <= m
0 <= skipB <= n
如果 listA 和 listB 没有交点，intersectVal 为 0
如果 listA 和 listB 有交点，intersectVal == listA[skipA] == listB[skipB]

进阶：你能否设计一个时间复杂度 O(m + n) 、仅用 O(1) 内存的解决方案？

解题思路：

这么多字，让我来给你翻译一下，就是要你判断两个链表是否相交，如果相交就返回它们第一次相交的节点地址
思路嘛，就是先分别遍历到两个链表的结尾，如果结尾节点地址都不同，那它们俩就不可能相交（因为一旦相交就无法分离了，不可能结尾节点地址都不同）。
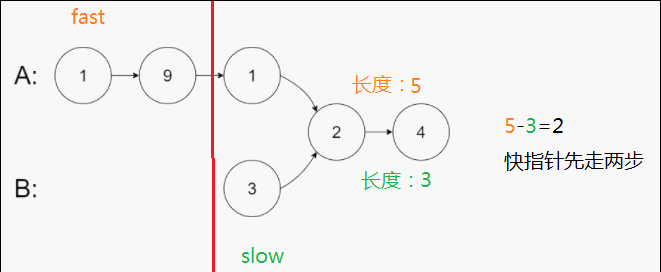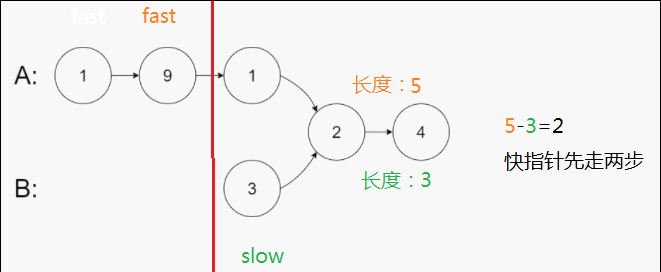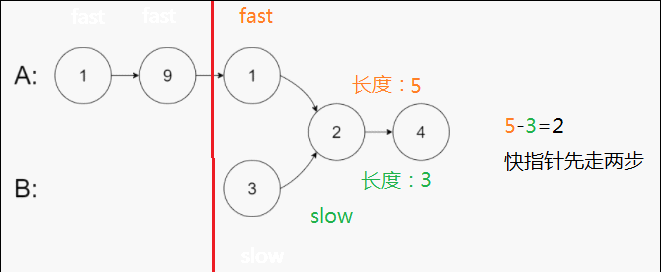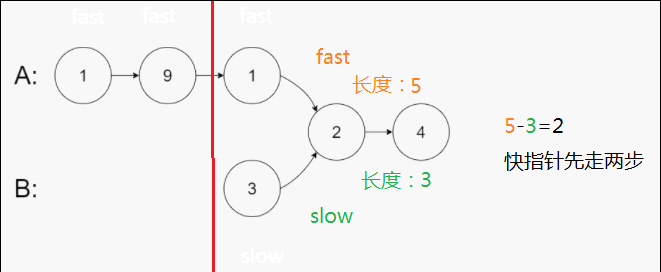
否则就用快慢指针去找它们第一次相交的节点地址，先让快指针走它们长度相差的步数，之后快慢指针一起走，它们第一次相同的地方就是要找的地址。

struct ListNode *getIntersectionNode(struct ListNode *headA, struct ListNode *headB) {
    struct ListNode* tailA, *tailB;
    int a = 1;
    int b = 1;
    tailA = headA;
    tailB = headB;
    //find tail
    while(tailA->next)
    {
        tailA = tailA->next;
        a++;
    }
    while(tailB->next)
    {
        tailB = tailB->next;
        b++;
    }
    if(tailA != tailB)
        return NULL;
    else
    {
        struct ListNode* longl = headB, *shortl = headA;
        if(a > b)
        {
            longl = headA;
            shortl = headB;
        }
        int c = abs(a - b);
        while(c--)
        {
            longl = longl->next;
        }
        while(longl)
        {
            if(longl == shortl)
            {
                return longl;
            }
            else
            {
                longl = longl->next;
                shortl = shortl->next;
            }
        }
    }
    return NULL;
}

链接：

力扣160. 相交链表

这一节我们介绍了快慢指针这一解题利器，还提到了相交链表、环形链表，之后还会出现更有趣的题目，敬请期待！