【机器学习】03. 支持向量机SVM库进行可视化分类(代码注释,思路推导)
目录
-
- 资源下载
- SVM库的基本介绍
- 1. 绘制所用的原始数据集的二维可视化图
-
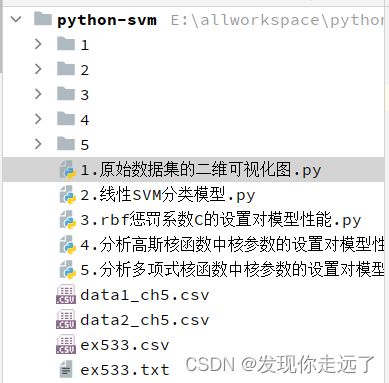
- (1)data1_ch5.csv的绘制
- (2)data2_ch5.csv的绘制
- (3)ex533.txt
- 2. 分析线性SVM模型对三种数据集的分类性能
-
- 分析
- 3. rbf选择径向基函数核函数的SVM模型惩罚系数C研究
-
- 分析
- 4. rbf选择径向基函数核函数的SVM模型核参数研究
-
- 分析
- 5. 多项式核函数的SVM模型核参数研究
-
- 分析
- 总结
『机器学习』分享机器学习课程学习笔记,逐步讲述从简单的线性回归、逻辑回归到 ▪ 决策树算法 ▪ 朴素贝叶斯算法 ▪ 支持向量机算法 ▪ 随机森林算法 ▪ 人工神经网络算法 等算法的内容。
欢迎关注 『机器学习』 系列,持续更新中
欢迎关注 『机器学习』 系列,持续更新中
资源下载
拿来即用,所见即所得。
项目仓库:https://gitee.com/miao-zehao/machine-learning/tree/master

SVM库的基本介绍
支持向量机算法被包含在 sklearn.svm 模块中,该模块提供了 7 个常用类
| SVM算法类别 | 描述 |
|---|---|
| LinearSVC类 | 基于线性核函数的支持向量机分类算法 |
| LinearSVR类 | 基于线性核函数的支持向量机回归算法 |
| SVC类 | 可选择多种核函数的支持向量机分类算法,通过“kernel”参数可以传入 |
| SVR类 | 可选择多种核函数的支持向量机回归算法 |
| NuSVC类 | 与 SVC 类非常相似,但可通过参数“nu”设置支持向量的数量。 |
| NuSVR类 | 与SVR类非常相似,但可通过参数“nu”设置支持向量的数量。 |
| OneClassSVM类 | 用支持向量机算法解决无监督学习的异常点检测问题 |
| text | 定义控件的标题文字 |
| state | 控制控件是否处于可用状态,参数值默认为 NORMAL/DISABLED,默认为 NORMAL(正常的) |
| width | 用于设置控件的宽度,使用方法与 height 相同 |
SVM 主要用于解决二分类的问题,上述表格中最常使用的是 SVC 类。下面对使用该算法的步骤进行总结:
- 读取数据,将原始数据转化为 SVM 算法所能识别的数据格式;
- 将数据标准化,防止样本中不同特征数值大小相差较大影响分类器性能;
- 选择核函数,在不清楚何种核函数最佳时,推荐使用“rbf”(径向基核函数)
- 利用交叉验证网格搜索寻找最优参数;(交叉验证的目的是防止过拟合,利用网格搜索可以在指定的范围内寻找最优参数)
- 使用最优参数来训练模型;
- 测试得到的分类模型。
- 此处引用了「站长严长生」的文章。
1. 绘制所用的原始数据集的二维可视化图
- 第一个数据集我们小试身手,常规的读取数据,注意绘图时要加入中文和负号的参数。
- 其实可以对数据进行前面线性回归逻辑回归一样的归一化处理,或是训练集的分割验证,但这里依据个人喜好有所取舍,最好还是有标准的流程。
(1)data1_ch5.csv的绘制
import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
# (1)data1_ch5.csv
#读取数据
data1_ch5_data=pd.read_csv("data1_ch5.csv").values
#把数据分成两类
list_zero=np.array([])
list_one=np.array([])
for i in data1_ch5_data:
if i[2]==0:
list_zero=np.append(list_zero,i)
elif i[2]==1:
list_one=np.append(list_one,i)
list_zero=list_zero.reshape(-1,3)#改变形状
list_one=list_one.reshape(-1,3)#改变形状
#设置绘图基本参数
plt.rcParams["font.sans-serif"]=["SimHei"] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号
plt.title("data1_ch5")
plt.xlabel("feature1")
plt.ylabel("feature2")
#绘制散点图:scatter
plt.scatter(list_one[:,0],list_one[:,1],c='red',label='x',marker = "x")
plt.scatter(list_zero[:,0],list_zero[:,1],c='blue',label='o',marker = "o")
plt.legend() # 显示图例
#展示图片并持久化保存
plt.savefig("1/"+"data1_ch5二维可视化图.png")
plt.show()
(2)data2_ch5.csv的绘制
作为一个程序员,不能老是CV代码,data1_ch5.csv和data2_ch5.csv的数据集结构相同,我们就封装一个函数,后面做题都可以调用函数来获取数据并绘制图片
import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
def drawMy(datafile):# 在(1)的基础上使用封装函数
#读取数据
data=pd.read_csv(datafile).values
#把数据分成两类
list_zero=np.array([])
list_one=np.array([])
for i in data:
if i[2]==0:
list_zero=np.append(list_zero,i)
elif i[2]==1:
list_one=np.append(list_one,i)
list_zero=list_zero.reshape(-1,3)#改变形状
list_one=list_one.reshape(-1,3)#改变形状
#设置绘图基本参数
plt.rcParams["font.sans-serif"]=["SimHei"] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号
plt.title(datafile)
plt.xlabel("feature1")
plt.ylabel("feature2")
#绘制散点图:scatter
plt.scatter(list_one[:,0],list_one[:,1],c='red',label='x',marker = "x")
plt.scatter(list_zero[:,0],list_zero[:,1],c='blue',label='o',marker = "o")
plt.legend() # 显示图例
#展示图片并持久化保存
plt.savefig("1/"+datafile+"二维可视化图.png")
plt.show()
drawMy("data2_ch5.csv")
(3)ex533.txt
作为一个程序员,哪怕数据集给的结构格式不一样,为了后续的工厂统一处理,这边建议处理掉数据集以适应我们前面写好的数据读取函数绘图函数。导出一个ex533.csv
#持久化保存ex533.csv,并且使之和data1_ch5.csv有一样的数据格式,可以调用我们前面封装的函数画图
ex533_csv_data=ex533_csv_data.reshape(-1,3)#改变形状
ex533_csv_data=pd.DataFrame(ex533_csv_data,columns=["feature1","feature2","label"],index=None)
ex533_csv_data.to_csv("ex533.csv",index=False)
drawMy("ex533.csv")#也可以调用前面的函数快速绘图了
完整代码如下:
# (3)ex533.txt
import pandas as pd
import numpy as np
import re #多个分隔符同时使用的库
from matplotlib import pyplot as plt
ex533_data=pd.read_csv("ex533.txt").values
#数据处理
list_zero = np.array([])
list_one = np.array([])
ex533_csv_data=np.array([])
for i in range(len(ex533_data)):
result_i=re.split("[ :]", ex533_data[i][0])#以空格和:作为分隔符,分割出数组
result_i=list(map(float, result_i))
#map映射函数,把列表中的字符串转为数字float类型 把float作用到result_i中的每一个元素
#封前 ['1 1:-0.347926 2:0.47076']
#分割后['1', '1', '-0.347926', '2', '0.47076']
#观察可知 0号索引数据表示分类y值,2号索引数据表示特征1数据,4号索引数据表示特征2数据
#把数据分成两类
if result_i[0]==-1:
list_zero=np.append(list_zero,np.array([result_i[2],result_i[4],result_i[0]]))
elif result_i[0]==1:
list_one=np.append(list_one,np.array([result_i[2],result_i[4],result_i[0]]))
#持久化保存ex533_csv数据的准备
ex533_csv_data=np.append(ex533_csv_data,np.array([result_i[2],result_i[4],result_i[0]]))
list_zero=list_zero.reshape(-1,3)#改变形状
list_one=list_one.reshape(-1,3)#改变形状
# 设置绘图基本参数
plt.rcParams["font.sans-serif"] = ["SimHei"] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号
plt.title("ex533")
plt.xlabel("feature1")
plt.ylabel("feature2")
# 绘制散点图:scatter
plt.scatter(list_one[:, 0], list_one[:, 1], c='red', label='x', marker="x")
plt.scatter(list_zero[:, 0], list_zero[:, 1], c='blue', label='o', marker="o")
plt.legend() # 显示图例
# 展示图片并持久化保存
plt.savefig("1/"+"ex533" + "二维可视化图.png")
plt.show()
#持久化保存ex533.csv,并且使之和data1_ch5.csv有一样的数据格式,可以调用我们前面封装的函数画图
ex533_csv_data=ex533_csv_data.reshape(-1,3)#改变形状
ex533_csv_data=pd.DataFrame(ex533_csv_data,columns=["feature1","feature2","label"],index=None)
ex533_csv_data.to_csv("ex533.csv",index=False)
drawMy("ex533.csv")#也可以调用前面的函数快速绘图了
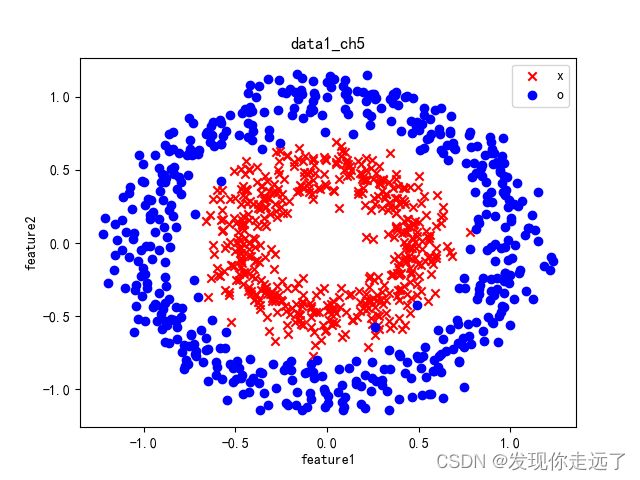
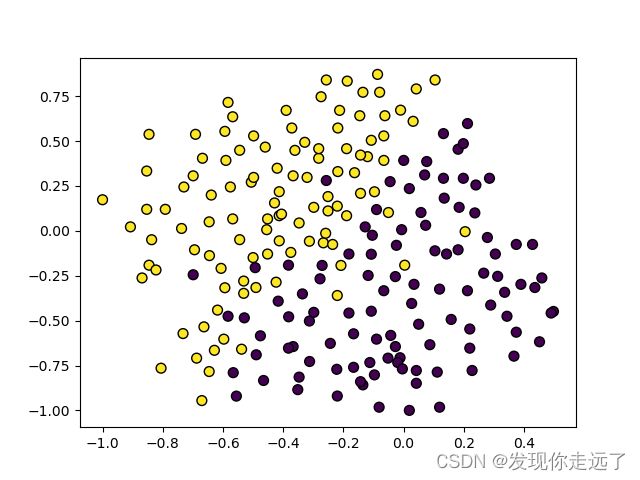
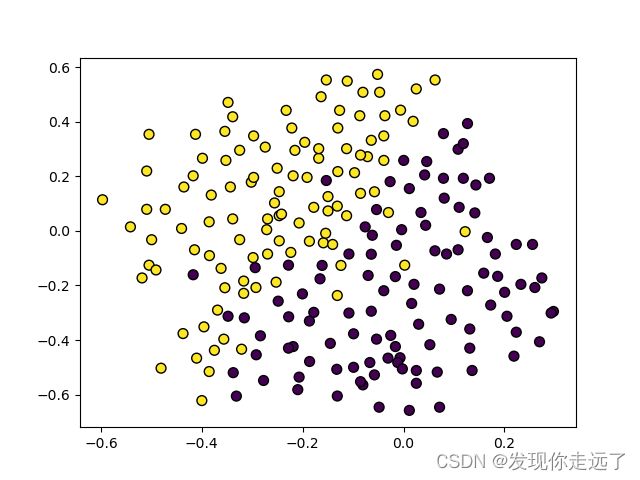
2. 分析线性SVM模型对三种数据集的分类性能
利用线性SVM建立’ex533.txt’、data1_ch5.csv、data2_ch5.csv等数据集的分类模型,分析线性SVM模型对这三种数据集的分类性能。
svm.SVC 支持向量机模型函数
svm.SVC(C=1.0, kernel=‘rbf’, degree=3, gamma=‘auto’, coef0=0.0, shrinking=True, probability=False, tol=0.001, cache_size=200, class_weight=None, verbose=False, max_iter=-1, decision_function_shape=None, random_state=None)
官方文档传送们
示例: clf = SVC(C=1,kernel=‘linear’,decision_function_shape=‘ovo’)#内核类型为线性
- C:浮动,可选(默认=1.0)误差项的惩罚参数 C。
- kernel:指定要在算法中使用的内核类型。它必须是“linear”、“poly”、“rbf”、“sigmoid”、“precomputed”或可调用对象之一。如果没有给出,将使用 ‘rbf’。如果给定了可调用对象,则它用于从数据矩阵中预先计算内核矩阵;该矩阵应该是一个 shape 数组(n_samples, n_samples)。
- linear:选择线性函数;
- polynomial:选择多项式函数;
- rbf:选择径向基函数;
- sigmoid:选择 Logistics 函数作为核函数;
- precomputed:使用预设核值矩阵,
- SVC 类默认以径向基函数作为核函数。
- decision_function_shape :默认决策函数分界线形状 ‘ovo’, ‘ovr’ or None, default=None
- fit_intercept:布尔值,默认值 真:指定是否应将常数(也称为偏差或截距)添加到决策函数中。
import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
from sklearn import preprocessing
from sklearn.datasets import load_iris # 导入鸢尾花数据集
from sklearn.svm import SVC #使用支持向量机算法
#封装一个模型训练函数,输入数据文件名即可完成训练并绘制图片
def my_train(datafile):
data=pd.read_csv(datafile).values
#数据归一化
max_abs_scaler = preprocessing.MaxAbsScaler() # 注册一个预处理对象
data = max_abs_scaler.fit_transform(data) # fit_transform(X[, y]) 适合数据,然后转换它。
X=data[:,0:2]
y=data[:,2].astype('int')
clf = SVC(C=1,kernel='linear',decision_function_shape='ovo')#内核类型为线性
#C:浮动,可选(默认=1.0)误差项的惩罚参数 C。
#kernel:指定要在算法中使用的内核类型。它必须是“linear”、“poly”、“rbf”、“sigmoid”、“precomputed”或可调用对象之一。如果没有给出,将使用 'rbf'。如果给定了可调用对象,则它用于从数据矩阵中预先计算内核矩阵;该矩阵应该是一个 shape 数组(n_samples, n_samples)。
# linear:选择线性函数;
# polynomial:选择多项式函数;
# rbf:选择径向基函数;
# sigmoid:选择 Logistics 函数作为核函数;
# precomputed:使用预设核值矩阵,
# SVC 类默认以径向基函数作为核函数。
# decision_function_shape :默认决策函数分界线形状 ‘ovo’, ‘ovr’ or None, default=None
#fit_intercept:布尔值,默认值 真:指定是否应将常数(也称为偏差或截距)添加到决策函数中。
# 训练模型,使用fit喂入数据X,y,即特征值和标签
clf.fit(X, y)
# 预测分类
result=clf.predict(X)
# 对模型进行评分
score=clf.score(X,y)
print(datafile+"线性SVM评分",score)
plt.figure()
# 分割图1行1列第一个图
plt.subplot(111)
# 选择X特征1和特征2进行绘图
plt.scatter(X[:,0],X[:,1],c =y.reshape((-1)),edgecolor='k',s=50)
plt.savefig("2/"+datafile + "线性SVM分类图.png")
plt.show()
my_train("data1_ch5.csv")
my_train("data2_ch5.csv")
my_train("ex533.csv")
分析
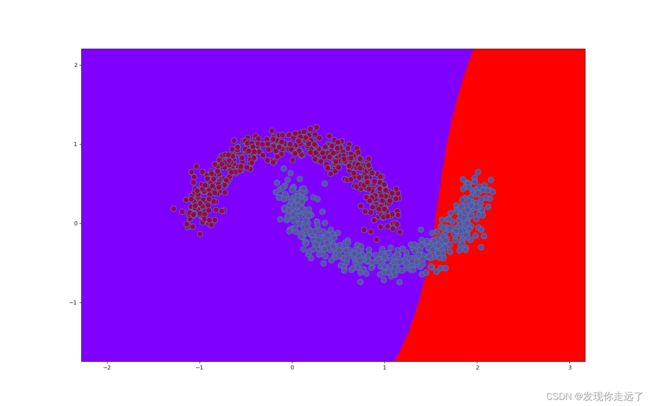
3. rbf选择径向基函数核函数的SVM模型惩罚系数C研究
基于案例5.3.3中的数据(‘ex533.txt’),设置5组不同的C值,建立基于高斯核函数的SVM模型(gamma设置为1),分别绘图画出二维数据图及决策分界线并进行性能比较,分析惩罚系数C的设置对模型性能的影响。
import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
from sklearn import preprocessing
from sklearn.datasets import load_iris # 导入鸢尾花数据集
from sklearn.svm import SVC #使用支持向量机算法
# 画出数据点和边界
def border_of_classifier(sklearn_cl, x, y):
"""
param sklearn_cl : skearn 的分类器
param x: np.array
param y: np.array
"""
## 1 生成网格数据
x_min, y_min = x.min(axis = 0) - 1
x_max, y_max = x.max(axis = 0) + 1
# 利用一组网格数据求出方程的值,然后把边界画出来。
x_values, y_values = np.meshgrid(np.arange(x_min, x_max, 0.01),
np.arange(y_min, y_max, 0.01))
# 计算出分类器对所有数据点的分类结果 生成网格采样
mesh_output = sklearn_cl.predict(np.c_[x_values.ravel(), y_values.ravel()])
# 数组维度变形
mesh_output = mesh_output.reshape(x_values.shape)
fig, ax = plt.subplots(figsize=(16,10), dpi= 80)
## 会根据 mesh_output结果自动从 cmap 中选择颜色
plt.pcolormesh(x_values, y_values, mesh_output, cmap = 'rainbow')
plt.scatter(x[:, 0], x[:, 1], c = y, s=100, edgecolors ='steelblue' , linewidth = 1, cmap = plt.cm.Spectral)
plt.xlim(x_values.min(), x_values.max())
plt.ylim(y_values.min(), y_values.max())
# 设置x轴和y轴
plt.xticks((np.arange(np.ceil(min(x[:, 0]) - 1), np.ceil(max(x[:, 0]) + 1), 1.0)))
plt.yticks((np.arange(np.ceil(min(x[:, 1]) - 1), np.ceil(max(x[:, 1]) + 1), 1.0)))
#封装一个模型训练函数,输入数据文件名即可完成训练
def my_train(datafile,C=1):
data=pd.read_csv(datafile).values
#数据归一化
# max_abs_scaler = preprocessing.MaxAbsScaler() # 注册一个预处理对象
# data = max_abs_scaler.fit_transform(data) # fit_transform(X[, y]) 适合数据,然后转换它。
X=data[:,0:2]
y=data[:,2].astype('int')
clf = SVC(C=C,kernel='rbf',decision_function_shape='ovr')#内核类型为rbf
# C:浮动,可选(默认=1.0)误差项的惩罚参数 C。
# kernel:指定要在算法中使用的内核类型。它必须是“linear”、“poly”、“rbf”、“sigmoid”、“precomputed”或可调用对象之一。如果没有给出,将使用 'rbf'。如果给定了可调用对象,则它用于从数据矩阵中预先计算内核矩阵;该矩阵应该是一个 shape 数组(n_samples, n_samples)。
# linear:选择线性函数;
# polynomial:选择多项式函数;
# rbf:选择径向基函数;
# sigmoid:选择 Logistics 函数作为核函数;
# precomputed:使用预设核值矩阵,
# SVC 类默认以径向基函数作为核函数。
# decision_function_shape :默认决策函数分界线形状 ‘ovo’, ‘ovr’ or None, default=None
# gamma: 高斯核函数,浮动,可选(默认='auto')'rbf'、'poly' 和 'sigmoid' 的核系数。如果 gamma 为“auto”,则将使用 1/n_features。
# fit_intercept:布尔值,默认值 真:指定是否应将常数(也称为偏差或截距)添加到决策函数中。
# 训练模型,使用fit喂入数据X,y,即特征值和标签
clf.fit(X, y)
# 预测分类
result=clf.predict(X)
# 对模型进行评分
score=clf.score(X,y)
print(datafile+"rbf内核SVM评分",score)
plt.figure()
# 分割图1行1列第一个图
plt.subplot(111)
# 选择X特征1和特征2进行绘图
# 原有的数据绘图
plt.scatter(X[:,0],X[:,1],c =y.reshape((-1)),edgecolor='k',s=50)
# 预测结果的绘图
# plt.scatter(X[:,0],X[:,1],c =result.reshape((-1)),edgecolor='k',s=50)
plt.savefig("3/" + "C={}{}文件原始数据图.png".format(C,datafile))
plt.show()
border_of_classifier(clf, X, y)
plt.savefig("3/" + "C={}ex533{}".format(C, "rbf内核SVM分类图.png"))
plt.show()
my_train("ex533.csv",C=0.01)
my_train("ex533.csv",C=10)
my_train("ex533.csv",C=1000)
分析
- 上图可以发现,随着C的变大从0.01到1000类别的划分愈发精准,更加泾渭分明,模型的评分也越来越高,从0.84逐渐达到0.93.
- 理论上C可以选择所有大于0的数。C越大表示整个优化过程中对于总误差的关注程度越高,对于误差的容忍能力越小。
- 当C趋于无穷大时,这个问题也就是不允许出现分类误差的样本存在,那这就是一个hard-margin SVM问题
- 当C趋于0时,我们不再关注分类是否正确,只要求类别间隔越大越好,那么我们将无法得到有意义的解且算法不会收敛
- 惩罚因子C的取值带来的影响:C越大,经验风险越小,结构风险越大,容易出现过拟合;C越小,模型复杂度越低,容易出现欠拟合。
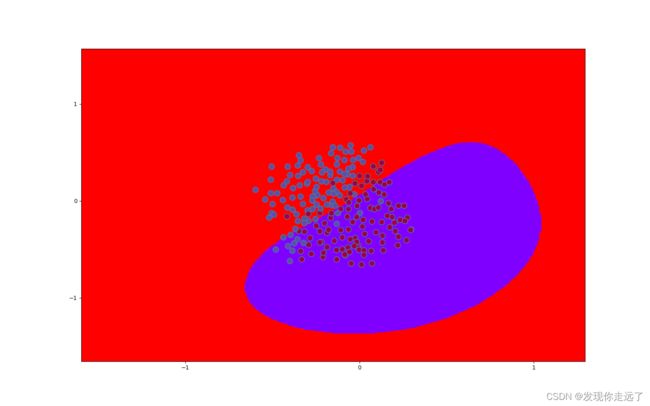
4. rbf选择径向基函数核函数的SVM模型核参数研究
基于数据集data1_ch5.csv(前两列为输入特征,最后一列的数据标签),通过设置不同的核参数建立基于高斯核函数的SVM模型,绘图画出二维数据图及决策分界线并进行性能比较,分析高斯核函数中核参数的设置对模型性能的影响。
import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
from sklearn import preprocessing
from sklearn.datasets import load_iris # 导入鸢尾花数据集
from sklearn.svm import SVC # 使用支持向量机算法
# 画出数据点和边界
def border_of_classifier(sklearn_cl, x, y):
"""
param sklearn_cl : skearn 的分类器
param x: np.array
param y: np.array
"""
## 1 生成网格数据
x_min, y_min = x.min(axis=0) - 1
x_max, y_max = x.max(axis=0) + 1
# 利用一组网格数据求出方程的值,然后把边界画出来。
x_values, y_values = np.meshgrid(np.arange(x_min, x_max, 0.01),
np.arange(y_min, y_max, 0.01))
# 计算出分类器对所有数据点的分类结果 生成网格采样
mesh_output = sklearn_cl.predict(np.c_[x_values.ravel(), y_values.ravel()])
# 数组维度变形
mesh_output = mesh_output.reshape(x_values.shape)
fig, ax = plt.subplots(figsize=(16, 10), dpi=80)
## 会根据 mesh_output结果自动从 cmap 中选择颜色
plt.pcolormesh(x_values, y_values, mesh_output, cmap='rainbow')
plt.scatter(x[:, 0], x[:, 1], c=y, s=100, edgecolors='steelblue', linewidth=1, cmap=plt.cm.Spectral)
plt.xlim(x_values.min(), x_values.max())
plt.ylim(y_values.min(), y_values.max())
# 设置x轴和y轴
plt.xticks((np.arange(np.ceil(min(x[:, 0]) - 1), np.ceil(max(x[:, 0]) + 1), 1.0)))
plt.yticks((np.arange(np.ceil(min(x[:, 1]) - 1), np.ceil(max(x[:, 1]) + 1), 1.0)))
# 封装一个模型训练函数,输入数据文件名即可完成训练
def my_train(datafile, myGamma):
data = pd.read_csv(datafile).values
# 数据归一化
# max_abs_scaler = preprocessing.MaxAbsScaler() # 注册一个预处理对象
# data = max_abs_scaler.fit_transform(data) # fit_transform(X[, y]) 适合数据,然后转换它。
X = data[:, 0:2]
y = data[:, 2].astype('int')
clf = SVC(C=1, kernel='rbf',gamma=myGamma, decision_function_shape='ovr') # 内核类型为rbf
# C:浮动,可选(默认=1.0)误差项的惩罚参数 C。
# kernel:指定要在算法中使用的内核类型。它必须是“linear”、“poly”、“rbf”、“sigmoid”、“precomputed”或可调用对象之一。如果没有给出,将使用 'rbf'。如果给定了可调用对象,则它用于从数据矩阵中预先计算内核矩阵;该矩阵应该是一个 shape 数组(n_samples, n_samples)。
# linear:选择线性函数;
# polynomial:选择多项式函数;
# rbf:选择径向基函数;
# sigmoid:选择 Logistics 函数作为核函数;
# precomputed:使用预设核值矩阵,
# SVC 类默认以径向基函数作为核函数。
# decision_function_shape :默认决策函数分界线形状 ‘ovo’, ‘ovr’ or None, default=None
# gamma: 高斯核函数,浮动,可选(默认='auto')'rbf'、'poly' 和 'sigmoid' 的核系数。如果 gamma 为“auto”,则将使用 1/n_features。
# fit_intercept:布尔值,默认值 真:指定是否应将常数(也称为偏差或截距)添加到决策函数中。
# 训练模型,使用fit喂入数据X,y,即特征值和标签
clf.fit(X, y)
# 预测分类
result = clf.predict(X)
# 对模型进行评分
score = clf.score(X, y)
print(datafile + "rbf内核SVM评分", score)
plt.figure()
# 分割图1行1列第一个图
plt.subplot(111)
# 选择X特征1和特征2进行绘图
# 原有的数据绘图
plt.scatter(X[:,0],X[:,1],c =y.reshape((-1)),edgecolor='k',s=50)
# 预测结果的绘图
# plt.scatter(X[:, 0], X[:, 1], c=result.reshape((-1)), edgecolor='k', s=50)
plt.savefig("4/" + "gamma={}{}文件原始数据图.png".format(myGamma,datafile))
plt.show()
border_of_classifier(clf, X, y)
plt.savefig("4/" + "gamma={}{}{}".format(myGamma,datafile,"rbf内核SVM分类图.png"))
plt.show()
my_train("data1_ch5.csv", myGamma=0.01)
my_train("data1_ch5.csv", myGamma=10)
my_train("data1_ch5.csv", myGamma=1000)
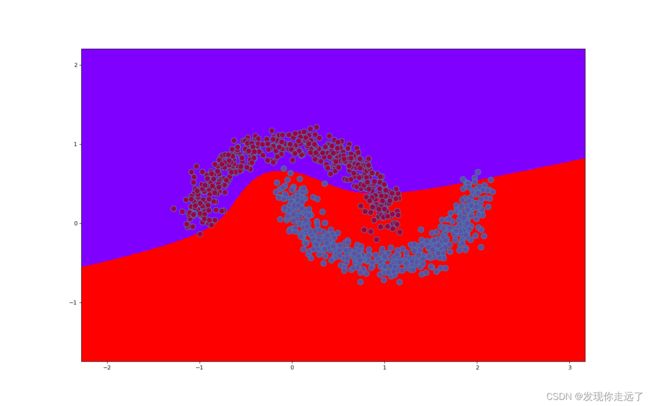
分析
gamma=0.01data1_ch5.csvrbf内核SVM分类图
在这里插入图片描述
-
随着高斯核函数的增大,模型精度提高了。模型的精度从0.732到0.999,虽然说这模型的精度确实是很高,但是我们明显可以发现过拟合的现象非常严重(过拟合就是模型只对于本数据集十分契合,但是很有可能换一个数据集就效果很差)这里分界线基本上和点完全重合,显然是不合理的。
-
高斯核的参数取值与样本的划分精细程度有关:越小,低维空间中选择的曲线越复杂,试图将每个样本与其他样本都区分开来;分的类别越细,容易出现过拟合;越大,分的类别越粗,可能导致无法将数据区分开来,容易出现欠拟合。
5. 多项式核函数的SVM模型核参数研究
基于数据集data2_ch5.csv(前两列为输入特征,最后一列的数据标签),通过设置不同的核参数建立基于多项式核函数的SVM模型,绘图画出二维数据图及决策分界线并进行性能比较,分析多项式核函数中核参数的设置对模型性能的影响。
import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
from sklearn import preprocessing
from sklearn.datasets import load_iris # 导入鸢尾花数据集
from sklearn.svm import SVC # 使用支持向量机算法
# 画出数据点和边界
def border_of_classifier(sklearn_cl, x, y):
"""
param sklearn_cl : skearn 的分类器
param x: np.array
param y: np.array
"""
## 1 生成网格数据
x_min, y_min = x.min(axis=0) - 1
x_max, y_max = x.max(axis=0) + 1
# 利用一组网格数据求出方程的值,然后把边界画出来。
x_values, y_values = np.meshgrid(np.arange(x_min, x_max, 0.01),
np.arange(y_min, y_max, 0.01))
# 计算出分类器对所有数据点的分类结果 生成网格采样
mesh_output = sklearn_cl.predict(np.c_[x_values.ravel(), y_values.ravel()])
# 数组维度变形
mesh_output = mesh_output.reshape(x_values.shape)
fig, ax = plt.subplots(figsize=(16, 10), dpi=80)
## 会根据 mesh_output结果自动从 cmap 中选择颜色
plt.pcolormesh(x_values, y_values, mesh_output, cmap='rainbow')
plt.scatter(x[:, 0], x[:, 1], c=y, s=100, edgecolors='steelblue', linewidth=1, cmap=plt.cm.Spectral)
plt.xlim(x_values.min(), x_values.max())
plt.ylim(y_values.min(), y_values.max())
# 设置x轴和y轴
plt.xticks((np.arange(np.ceil(min(x[:, 0]) - 1), np.ceil(max(x[:, 0]) + 1), 1.0)))
plt.yticks((np.arange(np.ceil(min(x[:, 1]) - 1), np.ceil(max(x[:, 1]) + 1), 1.0)))
# 封装一个模型训练函数,输入数据文件名即可完成训练
def my_train(datafile, myGamma):
data = pd.read_csv(datafile).values
# 数据归一化
# max_abs_scaler = preprocessing.MaxAbsScaler() # 注册一个预处理对象
# data = max_abs_scaler.fit_transform(data) # fit_transform(X[, y]) 适合数据,然后转换它。
X = data[:, 0:2]
y = data[:, 2].astype('int')
clf = SVC(C=1, kernel='poly',gamma=myGamma, decision_function_shape='ovr') # 内核类型为多项式
# C:浮动,可选(默认=1.0)误差项的惩罚参数 C。
# kernel:指定要在算法中使用的内核类型。它必须是“linear”、“poly”、“rbf”、“sigmoid”、“precomputed”或可调用对象之一。如果没有给出,将使用 'rbf'。如果给定了可调用对象,则它用于从数据矩阵中预先计算内核矩阵;该矩阵应该是一个 shape 数组(n_samples, n_samples)。
# linear:选择线性函数;
# polynomial:选择多项式函数;
# rbf:选择径向基函数;
# sigmoid:选择 Logistics 函数作为核函数;
# precomputed:使用预设核值矩阵,
# SVC 类默认以径向基函数作为核函数。
# decision_function_shape :默认决策函数分界线形状 ‘ovo’, ‘ovr’ or None, default=None
# gamma: 高斯核函数,浮动,可选(默认='auto')'rbf'、'poly' 和 'sigmoid' 的核系数。如果 gamma 为“auto”,则将使用 1/n_features。
# fit_intercept:布尔值,默认值 真:指定是否应将常数(也称为偏差或截距)添加到决策函数中。
# 训练模型,使用fit喂入数据X,y,即特征值和标签
clf.fit(X, y)
# 预测分类
result = clf.predict(X)
# 对模型进行评分
score = clf.score(X, y)
print(datafile + "多项式内核SVM评分", score)
plt.figure()
# 分割图1行1列第一个图
plt.subplot(111)
# 选择X特征1和特征2进行绘图
# 原有的数据绘图
plt.scatter(X[:,0],X[:,1],c =y.reshape((-1)),edgecolor='k',s=50)
# 预测结果的绘图
# plt.scatter(X[:, 0], X[:, 1], c=result.reshape((-1)), edgecolor='k', s=50)
plt.savefig("5/" + "gamma={}{}文件原始数据图.png".format(myGamma,datafile))
plt.show()
border_of_classifier(clf, X, y)
plt.savefig("5/" + "gamma={}{}{}".format(myGamma,datafile,"多项式内核SVM分类图.png"))
plt.show()
my_train("data2_ch5.csv", myGamma=0.01)
my_train("data2_ch5.csv", myGamma=0.1)
my_train("data2_ch5.csv", myGamma=1)
分析
- 随着核函数的增加,模型精度不断提高
- 分界线的样子也更加奇怪,逐渐从直线变成了非直线,逐渐的“曲线化”,逐渐复杂起来
总结
大家喜欢的话,给个,点个关注!给大家分享更多有趣好玩的python机器学习知识!
版权声明:
发现你走远了@mzh原创作品,转载必须标注原文链接
Copyright 2022 mzh
Crated:2022-9-23
欢迎关注 『机器学习』 系列,持续更新中
欢迎关注 『机器学习』 系列,持续更新中
【机器学习】01. 波士顿房价为例子学习线性回归
【机器学习】02. 使用sklearn库牛顿化、正则化的逻辑回归
【机器学习】03. 支持向量机SVM库进行可视化分类
【更多内容敬请期待】