RNN 的基本原理+pytorch代码
RNN 的基本原理+pytorch代码
文章目录
-
- RNN 的基本原理+pytorch代码
-
- 1.RNN模型的结构
- 2.模型输入(inputs)
- 3.隐藏层(hidden)
- 4.输出层(output)
- 5.反向传播
- 6.RNN的缺陷:长依赖问题
- 7.pytorch调用RNN
1.RNN模型的结构
传统的神经网络结构如下,由输入层,隐藏层和输出层组成
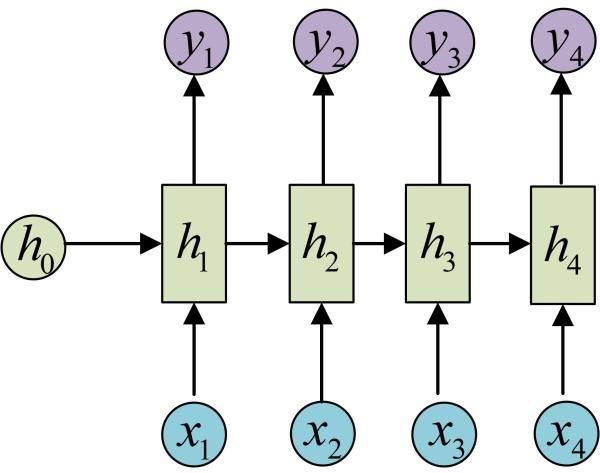
而RNN跟传统神经网络的最大区别在于每次都会将前一次的隐藏层结果带到下一次隐藏的计算中,如图所示:
如果我们将这个循环展开:
上图是一个二维的RNN模型的结构,RNN是循环神经网络,所指的xt和ht就是t时刻的输入,和t时刻对应的隐藏层,千万不要理解成隐藏层有t个隐藏单元。贴一个三维的RNN模型图出来方便理解。

举例:家里电脑坏了,我要拿去修,修好要200大洋。
此时,xt-1为电脑,ht-1=某件物品
xt为修,ht可以根据xt和ht-1学习到要去修电脑
xt+1为200大洋,ht+1可以学习到修xxx要200大洋
为啥ht+1不知道要修啥呢?200大洋和电脑之间距离太远忘记了(长依赖问题)。
2.模型输入(inputs)
RNN模型主要应用于时序型的数据,常见的应用类型为
a.如自然语言:你恰饭了没啊,x1为你,x2为恰…以此类推
b.股票价格,每日天气情况等
对于该类数据,传统模型无法表达前一个状态与后一个状态之间的连续性,故我们一般采用序列型的模型。
3.隐藏层(hidden)
弄清楚了模型输入后,继续了解隐藏层的内容,ht为t时刻输入x对应的隐藏单元
h t = t a n h ( U x t + W h t − 1 + b ) h_t=tanh(Ux_t+Wh_{t-1}+b) ht=tanh(Uxt+Wht−1+b)
其中
ht为t时刻时输入对应的隐藏单元的值;
U是输入层到隐藏层的权重矩阵;
W就是上一次隐藏层的值ht-1作为本次输入的权值矩阵。;
b为偏置量
4.输出层(output)
得到隐藏层的内容后即可计算输出结果
y t = s o f t m a x ( V h t + c ) y_t=softmax(Vh_t+c) yt=softmax(Vht+c)
其中
V是隐藏层到输出层的权重矩阵。
c为偏置量
注:在计算时,每一步使用的参数U、W、V、b、c都是一样的,也就是说每个步骤的参数都是共享的;
5.反向传播
其实反向传播就是对U、W、V、b、c求偏导,调整他们是的损失变小。
设t时刻,损失函数为
L t = 1 2 ( y t − y t ‘ ) 2 L_t=\frac12(y_t-y^‘_t)^2 Lt=21(yt−yt‘)2
则,损失函数之和为
L = ∑ t = 0 T L t L = \sum_{t=0}^T{L_t} L=t=0∑TLt
W在每一个时刻都出现了,所以W在t时刻的梯度=时刻t所有损失函数对对所有时刻的w的梯度之和:
∂ L ∂ W = ∑ t = 0 T ∂ L t ∂ W = ∑ t = 0 T ∑ s = 0 T ∂ L t ∂ W s \frac{\partial{L}}{\partial{W}} = \sum_{t=0}^T{\frac{\partial{L_t}}{\partial{W}} }=\sum_{t=0}^T{\sum_{s=0}^T{\frac{\partial{L_t}}{\partial{W_s}} }} ∂W∂L=t=0∑T∂W∂Lt=t=0∑Ts=0∑T∂Ws∂Lt
最后更新参数
W = W − α ∂ L ∂ W W=W-\alpha\frac{\partial{L}}{\partial{W}} W=W−α∂W∂L
接下来举个例子,t=2时刻U、V、W对于损失函数L2的偏导:
∂ L 2 ∂ U = ∂ L 2 ∂ y 2 ∂ y 2 ∂ h 2 ∂ h 2 ∂ U 2 + ∂ L 2 ∂ y 2 ∂ y 2 ∂ h 2 ∂ h 2 ∂ h 1 ∂ h 1 ∂ U 1 \frac{\partial{L_2}}{\partial{U}} = {\frac{\partial{L_2}}{\partial{y_2}} }{\frac{\partial{y_2}}{\partial{h_2}} }{\frac{\partial{h_2}}{\partial{U_2}} }+{\frac{\partial{L_2}}{\partial{y_2}} }{\frac{\partial{y_2}}{\partial{h_2}} }{\frac{\partial{h_2}}{\partial{h_1}} }{\frac{\partial{h_1}}{\partial{U_1}} } ∂U∂L2=∂y2∂L2∂h2∂y2∂U2∂h2+∂y2∂L2∂h2∂y2∂h1∂h2∂U1∂h1
∂ L 2 ∂ V = ∂ L 2 ∂ y 2 ∂ y 2 ∂ V \frac{\partial{L_2}}{\partial{V}} = {\frac{\partial{L_2}}{\partial{y_2}} }{\frac{\partial{y_2}}{\partial{V}} } ∂V∂L2=∂y2∂L2∂V∂y2
∂ L 2 ∂ W = ∂ L 2 ∂ y 2 ∂ y 2 ∂ h 2 ∂ h 2 ∂ W + ∂ L 2 ∂ y 2 ∂ y 2 ∂ h 2 ∂ h 2 ∂ h 1 ∂ h 1 ∂ W \frac{\partial{L_2}}{\partial{W}} = {\frac{\partial{L_2}}{\partial{y_2}} }{\frac{\partial{y_2}}{\partial{h_2}} }{\frac{\partial{h_2}}{\partial{W}} }+{\frac{\partial{L_2}}{\partial{y_2}} }{\frac{\partial{y_2}}{\partial{h_2}} }{\frac{\partial{h_2}}{\partial{h_1}} }{\frac{\partial{h_1}}{\partial{W}} } ∂W∂L2=∂y2∂L2∂h2∂y2∂W∂h2+∂y2∂L2∂h2∂y2∂h1∂h2∂W∂h1
以W,归纳总结后为
∂ L t ∂ W = ∑ t = 0 t ∂ L t ∂ y t ∂ y t ∂ h t ( ∏ j = k + 1 t t a n h ′ W ) ∂ h j ∂ W \frac{\partial{L_t}}{\partial{W}} = \sum_{t=0}^t{\frac{\partial{L_t}}{\partial{y_t}} }{\frac{\partial{y_t}}{\partial{h_t}} }(\prod_{j=k+1}^{t}{tanh'W}){\frac{\partial{h_j}}{\partial{W}} } ∂W∂Lt=t=0∑t∂yt∂Lt∂ht∂yt(j=k+1∏ttanh′W)∂W∂hj
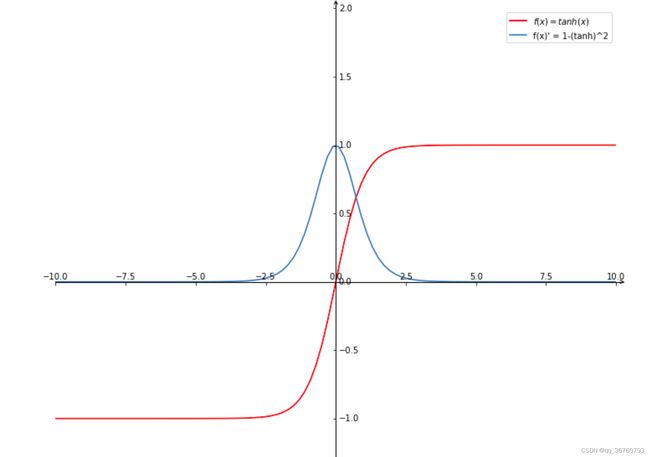
tanh函数及其导数图像
故,当t很大时,时间比较前的输入对当前损失的影响会很小,也就是梯度消失。
6.RNN的缺陷:长依赖问题
RNN的优势为可以利用过去的数据来推测当前数据的理解方式,但是由于RNN的参数是共享的,每一时刻都会由前面所有的时刻共同决定,这是一个相加的过程,这样的话就有个问题,当距离过长了,计算前面的导数时,最前面的导数就会消失或者爆炸,当但是当前时刻的整体梯度并不会消失,因为t时刻隐藏单元的值是1、2…t-1,时刻的值传过来的。且由于权值共享,所以整体的梯度还是会更新,通常在RNN中说的梯度消失是指后面的信息用不到前面的信息了。
所以当相关的数据离推测的数据越远时,RNN所能学习到的信息则越少。
例如:I live in Beijing. … .I can speak Chinese.
Beijing和Chinese是有着密切的关系的,但是由于中间存在着大量的句子,导致识别到Chinese无法和前面的Beijing产生联系。
7.pytorch调用RNN
![]()
#pytorch调用RNN代码
class RNN(nn.Module):
def __init__(self, input_size, output_size, hidden_dim, n_layers):
super(RNN, self).__init__()
#隐藏层特征数量
self.hidden_dim=hidden_dim
'''
input_size – 输入x中预期特征的数量
hidden_size – 隐藏状态h的特征数量
num_layers - 循环层数。例如,设置 num_layers=2意味着将两个RNN 堆叠在一起形成一个堆叠的RNN,第二个RNN接收 第一个RNN的输出并计算最终结果。默认值:1
nonlinearity — 隐藏层函数,可以是“tanh”或“relu”。默认值:'tanh'
bias - 如果为 False,则该层不使用偏差权重。默认值:真
batch_first - 输入特征是不是批量输入。默认值False
dropout - 是否要引入Dropout层,dropout概率等于dropout。默认值:0
bidirectional —如果为真,则成为双向 RNN。默认值:假
'''
self.rnn = nn.RNN(input_size, hidden_dim, n_layers, batch_first=True)
#全连接层
self.fc = nn.Linear(hidden_dim, output_size)
def forward(self, x, hidden):
#批量输入大小
batch_size = x.size(0)
#批量输入input,隐藏层参数
r_out, hidden = self.rnn(x, hidden)
#维度转化
r_out = r_out.view(-1, self.hidden_dim)
#全连接
output = self.fc(r_out)
return output, hidden
参考
1.pytorch RNN代码分析
2.如何从RNN起步,一步一步通俗理解LSTM
3.通俗易懂的RNN
4.Pytorch菜鸟入门(5)——RNN入门【代码】
5.【循环神经网络】5分钟搞懂RNN,3D动画深入浅出
如果内容有误或有侵权,请私信或者评论联系修改,感谢。