ICCV2017——图像反射去除与图像平滑基于一类深度架构

摘要： 本文提出了一种深度学习网络架构，用于提取底层视觉任务的边缘信息。不同于其他方法，本文只使用级联卷积层进行边缘估计与图像重建。本文应用于两个不同的边缘敏感的问题领域。本文提出用于弱监督的数据生成方法，解决了更多繁杂反射情况的问题。本文的方法以较大的优势取得了SOTA的效果。在所有情况中，网络架构都简单，快速且易于迁移。

一、简介
  受深度学习在大尺寸视觉图像复原任务上的巨大成功启发，大量的底层视觉任务，如图像去噪，图像阴影去除与图像平滑也应用了神经网络。考虑到图像边缘是一些问题的重要线索，网络可以代替计算复杂度高或不灵活的边缘滤波器。
  例如，图像平滑的根本目标是提取稀疏且显著的结构，如边缘与轮廓，并在低振幅的图像区域最小化颜色差异。为了使用神经网络估计不同边缘敏感图像的有效且快速的平滑滤波器，一般首先学习显著的梯度权重图，随后通过权重的优化过程或迭代处理对图像滤波。上述方法聚焦于使用朴素的CNN解决单一问题，然而，其并不适于更大的图像平滑或其他任务，如图像分层。
  后来，梯度域统计量相关的一种情况，在处理图像反射的过程中，如果只提供单一的照片，可能会存在部分离焦。当透过玻璃获取照片时，强光或者反射会影响到玻璃内的场景。有许多方法尝试削减这种影响，例如使用偏振片，在镜头前遮盖黑幕，使环境从暗到亮，或改变位置，这些在很多现实情况下是不可行的。此外，如果在飞机，博物馆，水族馆等相关的环境，只能通过玻璃拍摄照片，这时通常只能放大相机的光圈，模糊掉反射。
  为了从计算摄影的角度解决反射去除问题，传统图像模式假设获取的图像$\mathbf{I}$是背景图像$\mathbf{B}$与反射图像$\mathbf{R}$的线性组合，形如$\mathbf{I}=\mathbf{B}+\mathbf{R}$。显然，由于存在多可行解，这是一个病态问题，因此大多数反射移除算法需要多输入图像或用户交互标记反射与背景梯度，从而压缩可行解空间。然而，反射去除问题的一个可利用属性是两层的梯度或感知结构存在不同的分布，因为反射通常更加模糊。这自然的指向了可以使用数据驱动的网络的基于边缘的解决方法。
  本文提出了级联边缘与图像学习网络【Cascaded Edge and Image Learning Network，CEILNet】，用于解决不同的图像处理任务，如图像分层与图像滤波。依赖于基本的一类框架，通过特定域边缘的信息，可以用于各种实例。核心框架以一种直觉的方法运作。简而言之，将直接推测图像的困难任务分为两个子问题：通过深度有监督网络推测图像边缘图；通过推测的边缘图复原图像。其通过端到端的级联的两个相似的简单CNNs，且不需要人工构造模块。边缘图代表了特定任务图像邻域像素的颜色差异，而不是边缘检测问题中的稀疏显著结构。
  当然，这些目标需要大量的训练数据使得其在实践中可行。对于图像平滑，如果提供足够的计算资源用于产生样本，那么数据就不是重要的问题。然而，对于图像分层问题，真实数据的样本是匮乏的。因此提出弱监督学习方法用于训练反射去除，这涉及通过模拟自然场景的物理特性产生的反射使图像失真。
  总而言之，本文的贡献如下：
  -提出新的一类级联边缘与图像学习网络【CEILNet】，其仅仅依赖卷积层，不凭借任何人工构建，使用特定的组件，用于解决特定的边缘敏感图像处理任务。其架构迅速且可扩展，易于复制，促进不同底层视觉任务的转换；
  -首次使用深度学习解决单图像反射去除的图像分层问题，并提出了结合CEILNet的弱监督学习策略；
  -除了反射去除，本文展示了使用CEILNet在图像平滑任务上SOTA的视觉与数值表现，远远超越了以往的方法。

---

二、相关工作

---

三、网络架构
  本文的网络包含两个级联的子网络：一个边缘预测网络E-CNN，一个图像复原网络I-CNN。图1是架构的图解，对于反射去除与图像平滑均无改动。

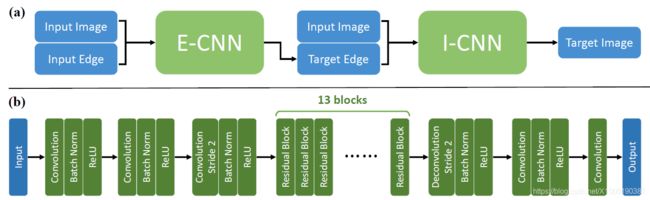
  图1，深度学习网络架构CEILNet。a.级联边缘与图像推测流程，两个CNN网络，E-CNN与I-CNN分别用于边缘推测与图像复原。I-CNN将E-CNN的输出作为输入，形成端到端与全卷积方案。b.E-CNN与I-CNN的详细CNN架构。

3.1 E-CNN边缘推测网络
  当处理边缘敏感图像处理任务时，例如反射去除与图像平滑，边缘相关的线索利用诸多算法。相似的，对于一个源图像${\mathbf{I}}^s$，使用CNN从目标图像${\mathbf{I}}^t$学习边缘图${\mathbf{E}}^t$。注意目标时推测目标图像的边缘，而不是输入图像，关键是不要把这种方法与传统的边缘检测相混淆。
  本文的工作中，边缘图不是二值的，因为根据经验，二值边缘图对于图像复原的信息较少。反之，本文设计了简单但是有效的边缘式：中心像素与其四邻域的颜色差异的绝对均值。特别的，图像$\mathbf{I}$的边缘图$\mathbf{E}$计算形如$${\mathbf{E}}_{x,y}=\frac{1}{4}\sum _c(|{\mathbf{I}}_{x,y,c}-{\mathbf{I}}_{x-1,y,c}|+|{\mathbf{I}}_{x,y,c}-{\mathbf{I}}_{x+1,y,c}|+|{\mathbf{I}}_{x,y,c}-{\mathbf{I}}_{x,y-1,c}|+|{\mathbf{I}}_{x,y,c}-{\mathbf{I}}_{x,y+1,c}|)\text{\hspace{1em}(1)}$$其中，$x,y$是像素坐标，$c$是RGB颜色空间的通道。
  为了易于计算，令边缘图${\mathbf{E}}^s$作为源图像${\mathbf{I}}^s$的额外通道作为输入。其中的简单直觉是：无论是折射或是通过滤波处理图像的平滑，都可以认为是源图像的简化版本，而边缘图也粗略的是源图像边缘图的退化版本。注意到这样的论述不仅有更好的结果，并且显著的加速了训练的收敛。总而言之，E-CNN逼近如下函数$f$：$${\mathbf{E}}^t=f({\mathbf{I}}^s,{\mathbf{E}}^s)\text{\hspace{1em}(2)}$$

3.2 I-CNN图像复原网络
  第二个子网络I-CNN用于通过学习从E-CNN推测得到的目标边缘图${\mathbf{E}}^t$处理得到${\mathbf{I}}^s$。换言之，其逼近如下函数$g$：$${\mathbf{I}}^t=g({\mathbf{I}}^s,{\mathbf{E}}^t)\text{\hspace{1em}(3)}$$输入图像与目标边缘联结为4通道张量作为输入，类似于E-CNN，因此其全局架构相同。此外，在图像平滑任务的基于边缘的图像重建步骤的上下文中，I-CNN是多功能的、数据驱动的传统滤波操作或基于优化的后处理结构的替代。

3.3 CNN层详述
  为了简便，如图1.b所示深度CNN的架构用于E-CNN与I-CNN。两个子网络只有输出通道数不同，E-CNN为1而I-CNN为3。在每种情况中，使用32个卷积层，每层使用相同的3x3核（除了倒数第三层），中间的30个卷积层均有64维的输入与输出特征图。前31层后接BN与ReLU，为了确保更好的上下文信息，通过将第三卷积层的步长设为2使中间特征图下采样到一半尺寸以放大感受野，并随后将倒数第三层的卷积层设为步长为2，核尺寸为4x4的反卷积层使得上采样回原尺寸。这在不丢失太多图像细节的前提下增大了感受野，并减少了计算复杂度。为了更好的结果与更快的收敛，中间26个卷积层实施为13个残差单元。
  最终，为了解决颜色退化问题，注意到在深度网络中，本文轻微的放大了推测图像${\mathbf{I}}^t$，通过$s_c=argmi{n}_{s_c}||{\mathbf{I}}_c^s-s_c\cdot {\mathbf{I}}_c^t|{|}_2^2$，且令${\mathbf{I}}_c^t\leftarrow s_c\cdot {\mathbf{I}}_c^t$。目标颜色修正通过I-CNN的自由参数层实施，其计算复杂度可以忽略。

---

四、网络训练
  首先展示训练网络，其应用了数据资源的独立性。随后描述了特定应用的生成训练数据的方法。

4.1 训练细节
  如图2所示，使用两个阶段的网络训练算法。首先使用图像真值与其边缘图分别训练子网络，确保各自的最优性。然后端到端的微调整个网络，保证子网络的联合。

  图2，两个阶段的网络训练算法。

  子网络最小化均方误差【Mean Squared Errors，MSE】，使用$\ast$表示真值，边缘推测的损失函数为$$L_E(\theta )=||{\mathbf{E}}^t-{\mathbf{E}}^{t\ast }|{|}_2^2\text{\hspace{1em}(4)}$$为了推测图像，不仅最小化颜色的MSE，还有梯度差：$$L_I(\theta )=\alpha ||{\mathbf{I}}^t-{\mathbf{I}}^{t\ast }|{|}_2^2+\beta (||{\nabla }_x{\mathbf{I}}^t-{\nabla }_x{\mathbf{I}}^{t\ast }|{|}_1+||{\nabla }_y{\mathbf{I}}^t-{\nabla }_y{\mathbf{I}}^{t\ast }|{|}_1)\text{\hspace{1em}(5)}$$梯度差似乎没有必要，但是其有助于防止深度卷积网络生成模糊图像。在联合训练阶段，最小化如下损失：$$L(\theta )=L_I(\theta )+\gamma L_E(\theta )$$对于反射去除与图像平滑，损失系数经验上设置$\alpha =0.2,\beta =\gamma =0.4$。
  初始化卷积权重，使用Adam训练网络，小批尺寸固定在1。当分别训练两个自网络时，学习率在初始迭代设置为0.01，对于反射去除和图像平滑，分别设置40和25轮次。全局网络的学习率下降至0.001。

4.2 训练数据生成
  带有真值背景图层的真实图像难以获取，一种简单的方法是使用不同的因子混合两个图像。其广泛的用于相关工作，但是如此生成的数据训练的网络对于真实图像的效果很差。因此本文提出新的生成方法以更加逼近真实世界的反射。
  假设反射相对于清晰的背景更加模糊，因为相机的焦点通常位于目标的背景。此外，相机放大光圈可以模糊掉反射。
  再考虑互补的观察，首先根据菲涅尔公式，当入射光穿过在兴趣区域前的具有不同折射率的媒介时，部分光会反射回像平面。然而，其可见性依赖于背景区域传播光的相对亮度。因此，预期上只有一部分传输的光会被反射光明显的阻挡，即使反射光均匀的分布在区域中。并且即使区域上有反射光，其强度可以是任意大的，单纯的加法模型对于弱反射成分并不总是符合物理的。
  基于上述观察，本文提出了如图3总结的新的方法，用于生成带有真实背景与反射光的图像。相比较单纯的混合，一个关键的区别是避免亮度溢出的方法并不是等比降低亮度，而是自适应的计算削减的值。基于此：无反射区与自然图像表现一致；强反射占据其他区域；反射的对比更好的被保持。也要注意到，高斯模糊核的值在$[2,5]$之间随机选取，本文更希望处理宽泛的现实情况，包括不是十分模糊的反射。图6顶部展示了4个生成的图像，图5展示了其与单纯混合的对比。
  要注意，生成图像作为弱监督的样本，而训练模型的最终展示使用具有自然反射的真实图像。

  图3，合成反射图像数据用于弱监督学习。减法与剪切操作使得反射强度在不同的区域饱和或消失。

---

五、实验
  本部分首先提出对比试验分析网络架构的设计选择，然后对比评估CEILNet与其他SOTA算法。

5.1 网络分析
  分析基于学习逼近$L_0$平滑的结果，使用100张PASCAL VOC测试图像。

  考察E-CNN的目标边缘图的重要性，移除E-CNN并训练单独的I-CNN模块。表1展示了使用推测边缘的I-CNN（即CEILNet）与使用输入图像边缘的I-CNN的显著差异。图4展示了视觉上的对比。
  反射去除也有相似的结果，推测背景边缘有利于图像分层。图5展示了典型的例子。
  考察I-CNN堆叠深度的问题，理想情况下足够深的网络可以隐式的处理目标边缘的推测。本文尝试训练一个更多卷积层的I-CNN，并发现在50层之后其表现迅速饱和。32层E-CNN与32层I-CNN组成的CEILNet表现比64层I-CNN表现要好（如表1所示）。
  考察I-CNN与传统方法，考虑使用域变换【Domain Transform，DT】代替I-CNN。E-CNN推测的目标边缘与输入图像共同作为DT的输入以平滑图像，同时也尝试将目标边缘真值，或者输入图像边缘作为DT的输入。表1展示了使用E-CNN推测边缘作为输入的I-CNN（即CEILNet）远远由于所有使用DT的结果。图4描绘了视觉对比效果。
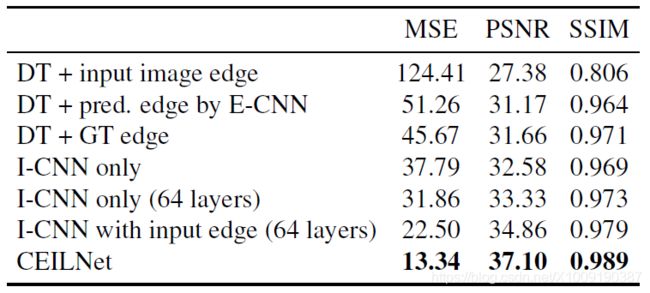  表1，图像平滑任务（学习$L_0$平滑）中的对比结果，CEILNet相比其他方法有极好的表现。
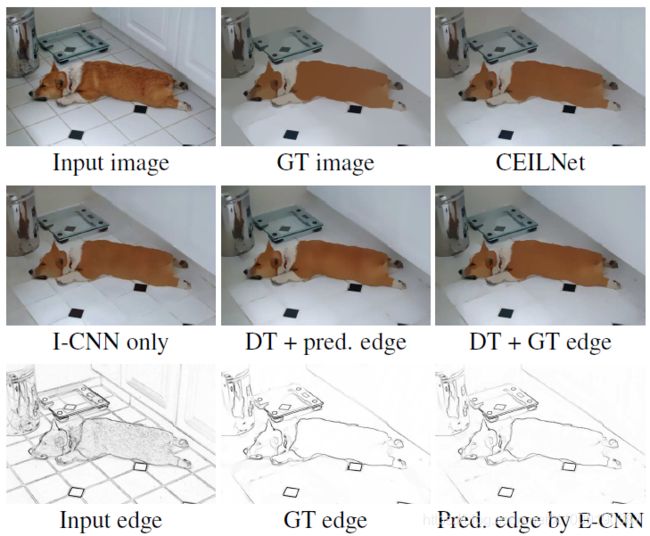  图4，图像平滑任务（学习$L_0$平滑）的质量对比，CEILNet相比其他方法生成更加令人满意的结果。
  图5，反射去除任务的质量对比，CEILNet相比于其他方法以及使用简单混合生成数据的方法移除更多的反射，并生成清晰的背景。

  对于反射去除，本文也尝试使用推测边缘作为其他图像分层算法的输入，并没有得到满意的结果。

5.2 反射去除
  训练数据使用4.2节的方法合成，自然图像共计17K张来源于PASCAL VOC数据集。两张自然图像用于生成一张合成图像，包含背景与反射图像，共生产8.5K张合成图像，分为7643张图像的训练集与850图像的测试集。训练图像被剪切为224x224，应用图2描述的算法，在训练的子任务中不曾发现过拟合。
  本文测试了CEILNet与SOTA的方法，为了量化比较，随机挑选了测试数据集的100张图像，评估算法推测得到的$\mathbf{B}$，表2展示了CEILNet的优秀表现。
  图6展示了合成与真实图像的定性的结果。反射图像通过计算$\mathbf{R}=\mathbf{I}-\mathbf{B}$得到，CEILNet能够分离折射图像并不破坏不存在反射失真的区域，即使数据十分明亮且光滑。
  图6，合成图像（顶部两行）与真实图像（底行）反射移除的定性结果。视觉上，本文的方法在不同情况下大量移除了反射并产生了良好的图像背景。最后实例的错误源于光的强反射与弱传播，但效果仍比其他方法好。

5.3 图像平滑
  训练数据使用PASCAL VOC数据集的17K张自然图像，通过图像平滑算法生成真值。这些图像不剪切的作为输入。随机选取PASCAL VOC的100张图像作为测试集。再次使用图2的算法训练网络。
  本文测试8种图像平滑算法，包括双边滤波器【Bilateral Filter，BLF】，迭代双边滤波器【Iterative Bilateral Filter，IBLF】，迭代引导滤波【Rolling Guidance Filter，RGF】，RTV纹理平滑，加权最小二乘平滑【Weighted Least Square Smoothing，WLS】，加权中值滤波【Weighted Median Filter，WMF】，$L_0$平滑与$L_1$平滑。
  表3描述了本文的方法与深度边缘感知滤波器在100张图像的测试集上的量化结果。无论在PSNR还是SSIM指标上，本文的方法表现均优于使用8种平滑算法种任何一个的深度边缘感知滤波器。本文也与基于混合神经网络的使用各种平滑算法的方法比较，表5展示了本文方法依然取得了更好的表现。

  表3，图像平滑任务的量化结果，包括8种平滑滤波的PSNR与SSIM指标，均值由前面的7种计算得到。

  表4，运行时间比较（以秒为单位），在各种情况下不同方法的比较。

  表5，图像平滑任务中本文的方法与其他方法的比较。

  图7展示了本文相比于其他方法的视觉结果，其视觉上更加接近于真值。

  图7，图像平滑任务的定性结果，所有的方法都逼近$L_0$平滑。视觉上，本文的方法更接近真值，数值展示了PSNR指标。

  本文在相同的计算机（NVIDA DGX-1）上八种传统平滑算法与三种基于深度学习的方法的时间复杂度。表4展示了本文的方法在大多数情况下更加迅速，可以在640x480的图像上以8fps的帧率逼近任何传统算法。

六、结论
  本文提出了CEILNet，一类深度框架用于边缘敏感图像的处理。首次使用基于学习的方法去除反射，并提出新的合成图像的方法。本文也基于DNN在图像平滑取得了SOTA的效果。