从零开始学Graph Database：什么是图

摘要：本文从零开始引导与大家一起学习图知识。希望大家可以通过本教程学习如何使用图数据库与图计算引擎。本篇将以华为云图引擎服务来辅助大家学习如何使用图数据库与图计算引擎。

本文分享自华为云社区《从零开始学Graph Database（1）》，作者：弓乙 。

基础概念

什么是图？

首先，我们需要明确图 Graph的概念。

这里的图，是graph, 是graphical，而不是graphic。即图处理的是关系问题，而不是图片。我们解决是关系问题，而非视觉cv问题。

在离散数据中，有专门研究图的图论。包含子图相关，染色，路径，网络流量等问题。

在计算机科学中，我们将图抽象为一种数据结构，即由点,边构成的集合。我们可以将现实世界的任意一种包含关系的实体用图来抽象概括。

我们通常把图的问题定义为G=(V,E,φ)：

V:是节点的集合
E:是边的集合
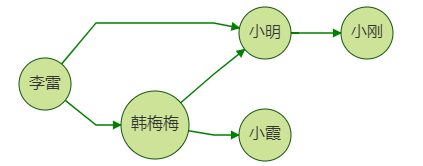
φ: E->{(x,y) | (x,y)∈ V^2 ∪ x≠y }是一个关联函数，它每条边映射到一个有顶点组成的有序对上。

下图是一个使用图来描述的社交网络。点代表了人，边代表了人和人之间为朋友关系。在构建了这样一个社交网络以后，我们可以通过使用图查询和算法使得图数据产生价值。如利用k跳查询,共同邻居,node2vec等来为社交网络中的用户进行好友推荐。

// 好友推荐逻辑
试想我们为李雷推荐好友，思路是：向他推荐其好友的好友。但是需要过滤掉本身李雷的好友。
如上图，小明即是李雷的好友，也是李雷好友的好友。所以在这种情况中，我们不需要再向李雷推荐小明了。
而是推荐 小霞和小刚。

这种稍微有点复杂的推荐思路，可以使用查询语言进行。
以gremlin为例：
g.V("李雷").repeat(out("friend").simplePath().where(without('1hop')).store('1hop')).
times(2).path().by("name").limit(100)

可以使用图做什么？

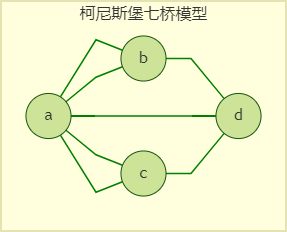
传统上我们使用图来解决一些数学问题。比如图论起源于著名的柯尼斯堡七桥问题, 该问题被欧拉推广为：怎样判断是否存在着一个恰好包含了所有边，且没有重复的路径。即一笔画问题。

欧拉证明了以下定理，并解决了一笔画问题：

连通的无向图G有欧拉路径（一笔画）的充要条件是：G中的奇点的数目等于0或2。

（奇点：连接边数为奇数的顶点。）

我们可以用一笔画问题来解决七桥问题，从模型可以看出来，七桥问题中的奇点数目为4个，显然不满足一笔画的充要条件。故七桥无法在所有桥都只能走一遍的前提下，把这个地方所有的桥都走遍。

当然了，图并非只能解决这类图论经典问题(如 四色问题，马的遍历问题，邮递员问题, 网络流问题 )，只要能够将研究对象表示为图结构，就能利用图的特点来解决问题，甚至大部分情况下，并不需要使用到多么高深的算法。

查询与算法

图查询

这里的查询一般指代使用原生图查询语言进行的图上对象的查询操作。如neo4j的Cypher，tinkerpop的Gremlin等。Cypher与Gremlin也是业界使用较多的查询语言，Cypher是侧重于pattern matching的声明式语言，而Gremlin则是基于groovy的函数式编程语言，强调graph traversal的重要性。

如：

1、gremlin

g.V("李雷").outE('friend').has('age',gt(30)).otherV().where(out('friend').(hasId('李雷'))).limit(100)

2、cypher

match (a)-[r1:friend]->(b)-[r2:friend]->(c) where a.mid='李雷' and r1.age>30 and a=c return id(b) limit 100

以上两种写法等价，只是使用的图查询语言有区别。

图算法

除了明确规则的查询外，我们也可以利用图算法对图进行分析。毕竟图中蕴含的信息量远比表面看上去多，这个时候我们希望通过图算法揭示图中更多的信息，如发现节点之间隐含关系，分析节点重要性，对业务场景进行行为预测等。

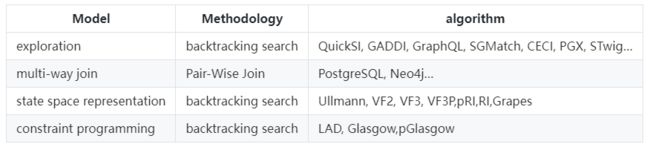
下表列出了目前不同类型具有代表性的图算法：

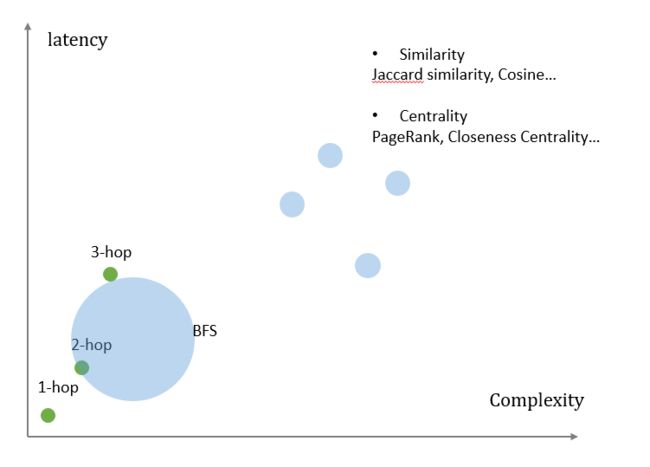
实际的场景中，我们需要同时兼顾算法的效果和执行成本。这也是很多使用场景所面临的trade-off问题。正如我们前面所说，大部分情况下不需要用到非常高深的图算法，特别是在在线任务中，我们更看重时延和效率。

亦或者说，在线场景中，重查询轻算法；而在离线场景中，重算法而轻查询。

事实上，图查询与图算法的边界并没有那么泾渭分明。或者说，图算法算是某种程度上的特殊图查询。我们普遍认为算法较查询需要更多的计算资源，会占用更多的CPU与内存。

比如上图的多跳查询和BFS algorithm，本质上是同一个查询。灰色模块显示的是gremlin与cypher的查询方法，蓝色模块显示的是不同图数据库中BFS算法的执行方式。但他们的结果都是一致的，均为点Tom的三度邻居。也就是在业界，N跳查询即可以作为广度/深度优先算法/khop算法单列出来，也可以作为图遍历/图查询中一种常用模式存在。

除此以外，subgraph matching也是一个图查询与图算法同时存在的研究课题。如上图，我们输入目标子图q，在图G中寻找其同构图，这其实是一个NP-Hard问题。

当然了，即使子图查询是一个非常困难的问题，大部分图查询语言还是提供了相应的match语法用于基于模式匹配的搜索功能，如neo4j使用的Cypher，或者支持指令式和声明式查询的Gremlin。而在图算法领域，subgraph matching则是一个极重要，极复杂的研究课题。下表中列出来一部分具有代表性的子图匹配算法的分类。(来源于paper[In-Memory Subgraph Matching: An In-depth Study])。

图的应用

下面让我们从一个具体的例子中体会一下图在场景中的使用。

假设我们需要在社交关系中为用户推荐好友，在不同的场景中，可以使用不同类别的查询和算法。如果用于在线推荐，我们可以将二度邻居作为其推荐结果，即2跳查询，这在大部分的图数据库中是一个代价非常小的查询，大多可在100ms以内完成，甚至可以在10ms内返回；如果用于离线推荐，则会倾向于使用推荐效果更优秀的图算法。例如，利用社团算法louvain, labelPropagation, Strongly Connected, k-Core获得每个点的社团分类，并将分类结果作为点上embedding的vector参与后续downstream task计算；或者直接使用图上Node embedding算法(Node2vec, FastRP, Weisfeiler-Lehman等)得到一个完整的点上Embedding的结果用于后续训练；当然，也可以直接使用图相似性算法(Cosine, Jaccard等)直接得到针对某个点的推荐结果。

gremlin: g.V('李雷').out().out()
cypher: match (n)--(m)--(l) where id(n)='李雷' return l


louvain:
[GES API]
POST /ges/v1.0/{project_id}/graphs/{graph_name}/action?action_id=execute-algorithm
{
    "algorithmName": "louvain",
    "parameters": {
        "max_iterations": "100",
        "convergence": "0.01",
        "weight":"score"
    }
}

大部分的工业使用场景中，图更多地扮演着数据库的角色，用来管理某个领域内的关系数据。用户大多看中图对于多跳关联分析能力，以及数据间脉络的整理归集，分析和可视化。

特别的，在某些垂直领域，由于其天生的关系结构，图数据库/图计算已经成为其不可或缺的工具了。如，在金融机构使用图来进行风控管理，通过对用户联系人交易等数据分析，识别欺诈借贷行为，规避恶意借贷风险，识别黑产群体等；或作为知识图谱的底层，提供快速关联查询，路径识别推荐，融合各种异构异质数据等。

为了更真实地体验图在各个行业的应用，也可以使用以下开箱即用的demo进行动手实践：

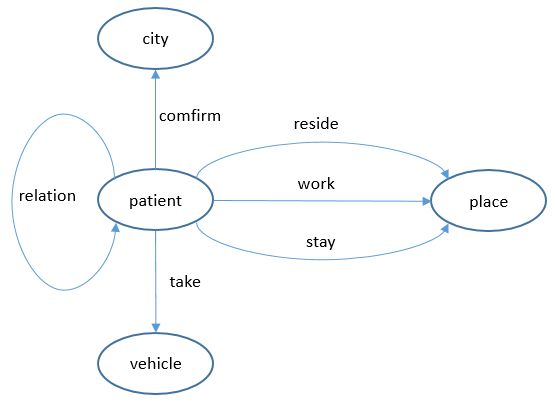
• 新冠患者轨迹追溯

• 电商风控案例

• 利用图数据库研究COVID-19论文数据集

• 教育知识图谱使用案例

以上案例提供了包括数据源，数据建模(schema)，云上创图，查询或分析演示等功能。

点击关注，第一时间了解华为云新鲜技术~