2022网鼎杯网络安全大赛白虎组部分Writeup

Misc

签到

知识竞赛题，提交答案抓包，遍历答案即可。

misc620

压缩包密码破解，尝试纯数字暴力破解，得到密码99114514。

解压得到一个csv表格和另一个加密的7z压缩包，打开表格查看：

在password字段发现疑似Base64编码字符，解码得到压缩包密码。

解压压缩包得到如下字符串：

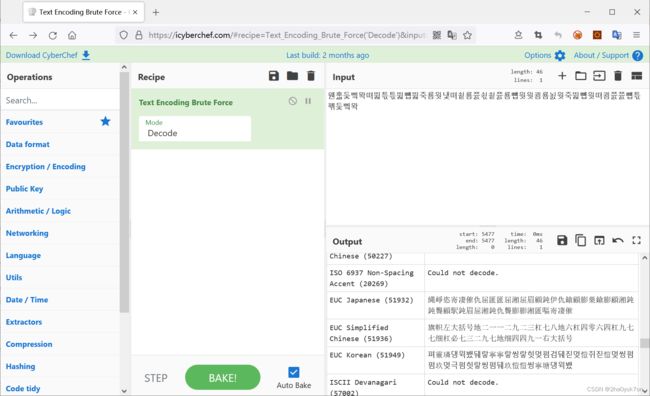
웬후ퟳ듳삨뫅뗘뛾튻튻뛾뻅뛾죽룜웟냋뗘쇹룜쯄쇣쇹쯄룜뻅웟웟쾸룜뇘웟죽뛾뻅웟뗘쾸쯄쯄뻅튻폒듳삨뫅

解对应编码得到flag：

Crypto

crypto582

题目文件：

from Crypto.Util.number import getPrime
import hashlib

e = 2022
m = getPrime(512)
m1 = getPrime(512)
m2 = getPrime(512)
flag = m + m1 + m2
flag = hashlib.md5(str(flag).encode('utf-8')).hexdigest()

c1 = pow(m+m1,e,m*m1)
c2 = pow(m+m2,e,m*m2)
c3 = pow(m1+m2,e,m1*m2)

x = pow(m1+2022,m,m*m1)
y = pow(m2+2022,m,m*m2)
z = pow(m+2022,m1,m*m1)

print('c1 =',c1)
print('c2 =',c2)
print('c3 =',c3)
print('x =',x)
print('y =',y)
print('z =',z)


'''
c1 =  85139434329272123519094184286276070319638471046264384499440682030525456122476228324462769126167628121006213531153927884870307999106015430909361792093581895091445829379547633304737916675926004298753674268141399550405934376072486086468186907326396270307581239055199288888816051281495009808259009684332333344687
c2 =  104554808380721645840032269336579549039995977113982697194651690041676187039363703190743891658905715473980017457465221488358016284891528960913854895940235089108270134689312161783470000803482494370322574472422461483052403826282470850666418693908817591349159407595131136843764544166774390400827241213500917391144
c3 =  94771625845449128812081345291218973301979152577131568497740476123729158619324753128517222692750900524689049078606978317742545997482763600884362992468406577524708622046033409713416026145377740182233674890063333534646927601262333672233695863286637817471270314093720827409474178917969326556939942622112511819330
x =  78237329408351955465927092805995076909826011029371783256454322166600398149132623484679723362562600068961760410039241554232588011577854168402399895992331761353772415982560522912511879304977362225597552446397868843275129027248765252784503841114291392822052506837132093960290237335686354012448414804030938873765
y =  100442166633632319633494450595418167608036668647704883492068692098914206322465717138894302011092841820156560129280901426898815274744523998613724326647935591857728931946261379997352809249780159136988674034759483947949779535134522005905257436546335376141008113285692888482442131971935583298243412131571769294029
z =  104712661985900115750011628727270934552698948001634201257337487373976943443738367683435788889160488319624447315127992641805597631347763038111352925925686965948545739394656951753648392926627442105629724634607023721715249914976189181389720790879720452348480924301370569461741945968322303130995996793764440204452
'''

分析题目文件，可得如下已知条件，其中$c_1、c_2、c_3、x、y、z$已知：

$c_1\equiv (m+m_1{)}^e(\mathrm{mod}m\ast m_1)$
$c_2\equiv (m+m_2{)}^e(\mathrm{mod}m\ast m_2)$
$c_3\equiv (m_1+m_2{)}^e(\mathrm{mod}{m}_1\ast m_2)$

$x\equiv (m_1+e{)}^m(\mathrm{mod}m\ast m_1)$
$y\equiv (m_2+e{)}^m(\mathrm{mod}m\ast m_2)$
$z\equiv (m+e{)}^{m_1}(\mathrm{mod}m\ast m_1)$

由费马小定理可得：
$c_1\equiv m_1^e(\mathrm{mod}m)$
$x\equiv (m_1+e)(\mathrm{mod}m)$
通过同余式变换构造等量关系：
$m_1^e\equiv c_1(\mathrm{mod}m)$
$m_1^e\equiv (x-e{)}^e(\mathrm{mod}m)$
根据同余式的交换性，有：
$(x-e{)}^e-c_1\equiv 0(\mathrm{mod}m)$

同理，也有：
$(y-e{)}^e-c_2\equiv 0(\mathrm{mod}m)$

因此求$(x-e{)}^e-c_1$和$(y-e{)}^e-c_2$的最大公约数即为$m$。

根据已知条件，可以得到$m_1、m_2$和$m$的关系：
$m_1\equiv (x-e)(\mathrm{mod}m)$
$m_2\equiv (y-e)(\mathrm{mod}m)$

这里需注意，$m_1、m_2$不一定比$m$小，即
$m_1=x-e+k_{1}m$
$m_2=x-e+k_{2}m$
其中，$k_1、k_2$为正整数。经过尝试，发现$k_1=0、k_2=1$。

同余：给定一个正整数m，如果两个整数a和b满足a-b能够被m整除，即(a-b)/m得到一个整数，那么就称整数a与b对模m同余，记作a≡b(mod m)。对模m同余是整数的一个等价关系。

EXP：

a1 = (x-e) ** e - c1
a2 = (y-e) ** e - c2

m = sympy.gcd(a1, a2)
m1 = (x - e) % m
m2 = (y - e) % m + m

flag = m + m1 + m2
flag = hashlib.md5(str(flag).encode('utf-8')).hexdigest()
print(flag)

Web

web923

扫描发现存在.git文件泄露。

重建还原代码，进行代码审计，发现关键文件application\index\controller\Index.php：

namespace app\index\controller;

class Index
{
    public function index()
    {
        return '
).'>
            
            ';

    }

    public function upload()
    {
        if (request()->isPost()){
            $file = $_FILES['hw_file']??'';
            if(!$file){
                return json(['code'=>0,'msg'=>'请选择文件']);
            }
            $file_name = $file['name'];
            $file_tmp = $file['tmp_name'];
            $file_size = $file['size'];
            if ($file_size > 1024*1024*2){
                return json(['code'=>0,'msg'=>'文件大小不能超过2M']);
            }
            $file_error = $file['error'];
            if ($file_error > 0){
                return json(['code'=>0,'msg'=>'上传失败']);
            }
            $file_type = $file['type'];
            $file_ext = explode('.',$file_name);
            $file_ext = strtolower(end($file_ext));
            if(strstr($file_type, "image/")){
                if($this->upload_as_image($file_ext, $file_tmp, "../uploads/images/".date('YmdHis')."/", ["gif"], request()->get("hw_file_name")??FALSE)){
                    return json(['code'=>1,'msg'=>'上传成功']);
                } else {
                    return json(['code'=>0,'msg'=>'上传失败']);
                }
            } else {
                if($this->upload_as_text($file_ext, $file_tmp, "../uploads/files/".date('YmdHis')."/", request()->get("hw_file_name")??FALSE)){
                    return json(['code'=>1,'msg'=>'上传成功']);
                } else {
                    return json(['code'=>0,'msg'=>'上传失败']);
                }
            }
        } else {
            return json(['code'=>0,'msg'=>'请求方式错误']);
        } 
    }

    public function upload_as_image($image_type, $image_tmp_file, $upload_base_dir, $file_ext_black_list, $image_filename=FALSE)
    {
        if(in_array($image_type, $file_ext_black_list)){
            return 0;
        }
        switch ($image_type) {
            case 'jpg':
                $image_ext = '.jpg';
                break;
            case 'png':
                $image_ext = '.png';
                break;
            case 'gif':
                $image_ext = '.gif';
                break;
            default:
                $image_ext = '.jpg';
                break;
        }
        $image_size = getimagesize($image_tmp_file);
        $image_width = $image_size[0];
        $image_height = $image_size[1];
        if($image_width > 200 || $image_height > 200){
            return 0;
        }
        if ($image_filename === FALSE) {
            $image_filename = date('YmdHis') . rand(1000, 9999) . $image_ext;
        } else {
            $image_filename = $image_filename . $image_ext;
        }
        if(!file_exists($upload_base_dir)){
            mkdir($upload_base_dir, 0777, true);
        }
        $image_file_path = $upload_base_dir . $image_filename;
        rename($image_tmp_file, $image_file_path);
        return 1;
    }

    public function upload_as_text($text_type, $text_tmp_file, $upload_base_dir, $text_filename=FALSE)
    {
        if(strstr($text_type, "ph")  || in_array($text_type, ['php', 'html', 'js', 'css', 'sql', 'phtml', 'shtml', 'php5', 'php7', 'phtm', 'pht', 'php8', 'php4', '.htaccess', 'tpl'])){
            return 0;
        }
        if (strstr($text_filename, ".") || strstr($text_filename, "/")) {
            return 0;
        }
        if( strlen($text_type) == 0){
            $text_ext = "";
        } else {
            if(!ctype_alpha($text_type)){
                return 0;
            }
            $text_ext = "." . $text_type;
        }
        if ($text_filename === FALSE) {
            $text_filename = date('YmdHis') . rand(1000, 9999) . $text_ext;
        } else {
            $text_filename = $text_filename . $text_ext;
        }
        if(strlen($text_filename) == 0 || strstr($text_filename, "/") ||!preg_match('/[A-Za-z0-9_]/is', $text_filename)){
            return 0;
        }
        if(!file_exists($upload_base_dir)){
            mkdir($upload_base_dir, 0777, true);
        }
        $text_file_path = $upload_base_dir . "/" . $text_filename;
        rename($text_tmp_file, $text_file_path);
        return 1;
    }
    
}

是一个文件上传功能，经过代码审计，可以发现有如下逻辑：

1. 通过Content_type字段判断上传文件类型，若是image/类型，则进入上传图像逻辑；否则进入上传文件逻辑；
2. 上传图像文件扩展名只能是jpg、png、gif，其他扩展名默认修改为jpg;
3. 上传文件进行了扩展名的白名单校验，但这里有个逻辑漏洞，校验的是文件名点号后.的值，因此若文件名为.htaccess时，是可以绕过校验的；
4. 上传后的文件路径存放在uploads/images/yyyyMMddHHmmss/下，时间即上传请求的时间，若上送hw_file_name字段，则文件名为该字段值；

综上，利用思路为同时上传.htaccess和木马文件，因为需要确保两个文件在同一目录下，然后连接木马文件即可。

.htaccess上传漏洞原理请见我的另一篇博客：
文件上传漏洞之.htaccess文件解析漏洞-2ha0yuk7on.