强化学习DQN、DDQN和Dueling DQN的原理介绍与PARL核心代码解析
摘要
本文主要介绍DQN算法的基本原理,以及在它基础上改进的DDQN和Dueling DQN,介绍完后会结合对应的PARL代码进行解析说明(PARL 是一个高性能、灵活的强化学习框架)。
三篇相关的论文地址如下,接下去的三个小节会围绕这三篇论文的重点部分进行剖析。
DQN:Human-level Control Through Deep Reinforcement Learning
DDQN:Deep Reinforcement Learning with Double Q-learning
Dueling DQN: Dueling Network Architectures for Deep Reinforcement Learning
DQN
DQN的全称是deep Q-network,顾名思义,是一种深层神经网络的算法,用来预测Q值的大小。Q值可以理解为状态动作价值,即智能体在某一状态下执行该动作所带来的预期收益。
通俗一点来解释Q值的话,我们假设有个无所不知的上帝和一个普通的凡人。在凡人当前处于某一状态s时,凡人可以从一定范围的动作(如a、b、c)中选择一个执行,而上帝则会根据凡人的选择给出一个分数(因为上帝无所不知,所以知道凡人在选择了某个动作之后会发生的所有事情)。比如凡人选择了a,上帝会给出80分,选择b的话上帝会给70分,选择c的话上帝会给60分,那么凡人在当前状态下肯定会选择分数最高的a选项。在强化学习中,智能体就是前面所说的凡人,只要智能体知道了所有的Q值,他就能根据Q值的大小做出当前状态下最优的选择。
所以DQN的目标就是训练出一个优秀的神经网络,该神经网络的输入是s(当前所处状态state),输出的是n个Q值(n代表可选择的动作个数,输出的实际上是一个n维的向量)。这样智能体就能在每次做选择前,把当前所处状态输入神经网络后,根据神经网络的输出,选择输出中最大的Q值所对应的动作。然后智能体进入下一状态,把下一状态输入神经网络,根据神经网络的输出选择下一动作,…,如此不断循环往复,直到游戏结束。
论文中给出的Q值计算公式如下: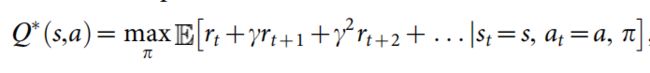
其实指的就是智能体在当前状态s下,选择动作a时所对应的Q(s,a)等于当前时刻所取得的奖励 r t r_t rt加上之后所能取得的最大奖励。
于是可以根据如下公式更新神经网络的参数:

仔细看这个公式其实就是利用的MSE损失函数。每次只要传入一组(s,a,r,s’),即当前所处状态s,当前选择的动作a,做出动作a后获得的奖励r,以及做出动作a后转移到的下一状态s’。这四个值都可以在模拟一局游戏时取到,而且每模拟一局游戏能取到非常多组数据。在论文中作者提出了经验回放(experience replay)的采集数据方法,即事先采样足够多组的数据放入一个固定容量的经验池中,然后每次训练时从该经验池中随机取出一个batch的数据进行梯度下降更新参数。值得注意的是这一个batch的数据训练完成后是放回经验池的,也就是说下次训练时是可以复用的。只有当产生新的数据时,才会更新经验池。当一轮训练完成,更新完模型参数后,再根据该模型提供的策略进行模拟游戏,产生新的数据并放入经验池中,由于该经验池是有最大容量的,所以最早的一些数据会被新的数据替代。像这样每玩几局游戏训练一次(玩游戏的同时其实是在更新训练数据),极大地提升了训练的效率。此外,为了更加稳定地训练模型,作者提出了固定target值的思想,具体做法是复制一个和原本Q网络一模一样的target-Q网络用于计算target值,使得target-Q网络的参数在一定时间段内保持固定不变,在这段时间内用梯度下降训练Q网络。然后阶段性地根据Q网络学习完后的参数更新这个target-Q网络(就是把Q网络的参数再复制过去)。整个训练过程如下:

具体的神经网络结构如下图所示:
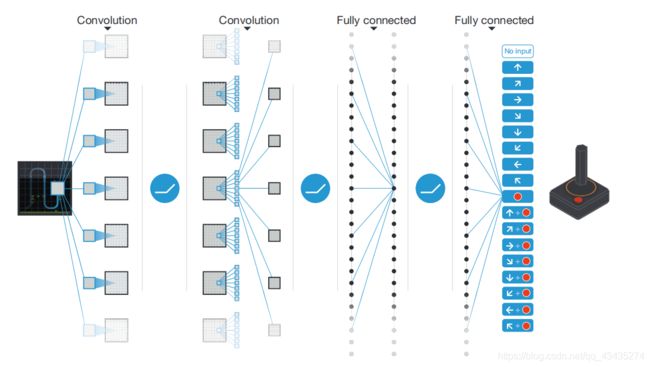
输入一张图像代表当前所处状态,然后经过两个卷积层和两个全连接层,最后输出一个n维的结果(n代表可选动作个数)。图中n的值为18,分别代表了可选的18种手柄动作。
论文中作者还根据训练完成后的神经网络中最后一个隐层的embedding利用t-SNE画出了二维可视化结果图:

从图中我们可以明显看出聚集在一起的embedding所对应的游戏状态是差不多的,刚开始的游戏状态聚集在一起,快死了的游戏状态聚集在一起,说明该神经网络在不断地通过SGD更新参数后已经学得了很多东西。

论文最后还给出了用DQN训练出的agent与人类玩家的对比。可以看出通过该算法训练的模型也在很多其它游戏中取得了十分不错的分数,有些游戏得分甚至超过了人类玩家。
DDQN
DDQN是Double DQN的缩写,是在DQN的基础上改进而来的。DDQN的模型结构基本和DQN的模型结构一模一样,唯一不同的就是它们的目标函数。
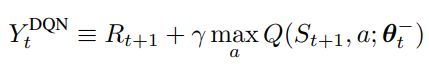

这两个target函数的区别在于DoubleDQN的最优动作选择是根据当前正在更新的Q网络的参数 θ t \theta_t θt,而DQN中的最优动作选择是根据上一小节提到的target-Q网络的参数 θ t − \theta_t^- θt−。
这样做的原因是传统的DQN通常会高估Q值的大小(overestimation)。

而DDQN由于每次选择的根据是当前Q网络的参数,并不是像DQN那样根据target-Q的参数,所以当计算target值时是会比原来小一点的。(因为计算target值时要通过target-Q网络,在DQN中原本是根据target-Q的参数选择其中Q值最大的action,而现在用DDQN更换了选择以后计算出的Q值一定是小于或等于原来的Q值的)这样在一定程度上降低了overestimation,使得Q值更加接近真实值。

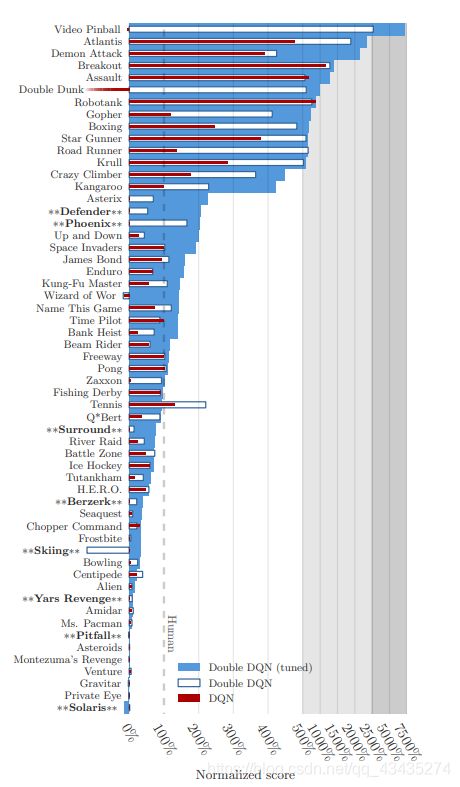
论文最后作者也给出了用DQN和DDQN训练出的agent玩Atari游戏的对比图,从图中可以看出在大多数游戏的表现上来看,利用DDQN训练出的效果对比DQN在得分上是有显著提升的。
Dueling DQN
Dueling DQN也是在DQN的基础上进行的改进。改动的地方是DQN神经网络的最后一层,原本的最后一层是一个全连接层,经过该层后输出n个Q值(n代表可选择的动作个数)。而Dueling DQN不直接训练得到这n个Q值,它通过训练得到的是两个间接的变量V(state value)和A(action advantage),然后通过它们的和来表示Q值。
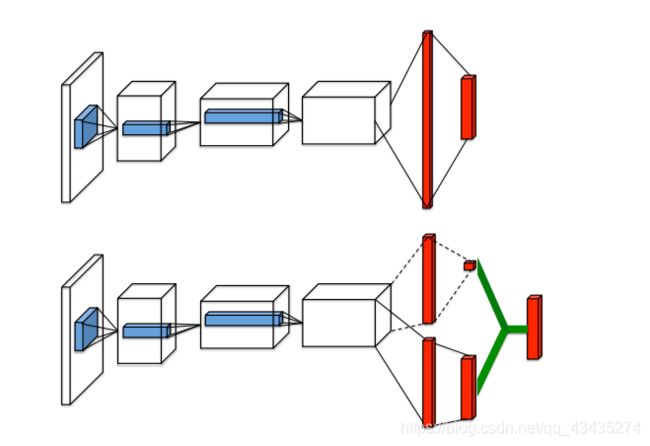
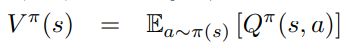
![]()
仔细想想这么拆分还是很有道理的。V代表了在当前状态s下,Q值的平均期望(综合考虑了所有可选动作)。A代表了在选择动作a时Q值超出期望值的多少。两者相加就是实际的Q(s,a)。就像当人看到某一游戏画面时是可以大概判断出当前局势的好坏,然后再根据每一种选择看哪一种action对当前局势增益最多。V就是当前局势,A就是对当前局势的增益。所以这样设计模型就是为了让神经网络对给定的s有一个基本的判断,在这个基础上再根据不同的action进行修正。
但是按照上述想法直接训练是有问题的,问题就在于若神经网络把V训练成固定值0后,就相当于普通的DQN网络了,因为此时的A值就是Q值。所以我们需要给我们的神经网络加一个约束条件,让所有动作对应的A值之和为零,使得训练出的V值是所有n个Q值的平均值(n代表可选择的动作个数)。论文中的具体做法是利用下图中的公式给到约束。

公式里括号中的部分其实就是之前说的A值,公式里的|A|代表了可选择动作的个数(就是上一段的n)。可以明显看出若把|A|个动作对应的括号中的部分相加,它们的和为零。所以问题就转化为利用神经网络求上述公式中的V(s; θ \theta θ, β \beta β)与A(s,a; θ \theta θ, α \alpha α)。其中V(s; θ \theta θ, β \beta β)就是前文所提到的V值,而A(s,a; θ \theta θ, α \alpha α)和前文所提到的广义上的A值其实不一样,但可以通过A(s,a; θ \theta θ, α \alpha α)计算出A值。
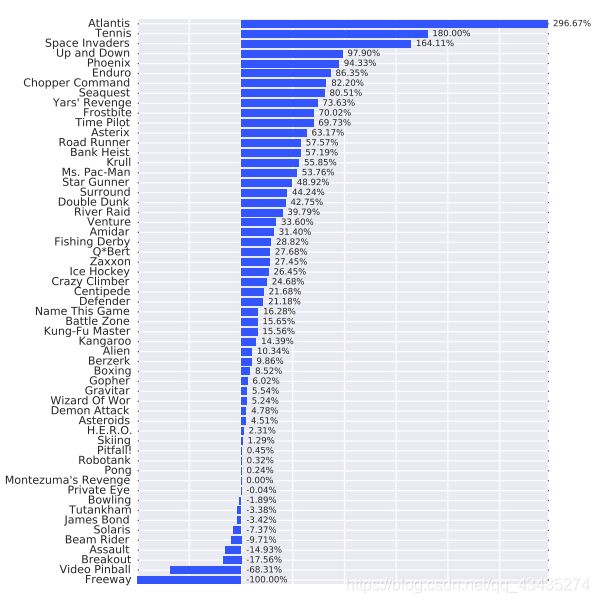
下图为用Duel方法增加这两个间接层后与之前直接单层输出结果的对比。可以看出在大多数游戏的表现上采用Duel方法后的网络模型所取得的成绩是更好的,最好的成绩接近改进前的三倍之多。
PARL代码解析
PARL 作为一个高性能、灵活的强化学习框架,能很方便地实现上述提到的三种算法,下面结合PARL官方给出的example,看看如何利用PARL复现出DQN、DDQN和Dueling DQN,完整代码github地址如下:DQN_variant
先看一下模型层的代码。这里是把三种算法封装在一个模型里了,实际调用时可以通过algo参数传入希望使用的算法名。DQN和DDQN的网络结构是一致的(区别体现在算法层里),所以只要通过根据algo参数的传入来区分判断是不是‘Dueling’从而选择不同的网络结构。基础的DQN这里采用了四个卷积层提取特征,然后经过一个全连接层最后输出act_dim维的结果。若使用的是Dueling DQN,一开始的四个卷积层还是和前面一样,不同的是在经过卷积层提取完特征后,分别用了两个全连接层计算state value(1维)和advantages(act_dim维),最后利用广播的性质加在一起使得最终结果也是act_dim维。
class AtariModel(parl.Model):
def __init__(self, act_dim, algo='DQN'):
self.act_dim = act_dim
# 先都经过四层卷积的特征提取
self.conv1 = layers.conv2d(
num_filters=32, filter_size=5, stride=1, padding=2, act='relu')
self.conv2 = layers.conv2d(
num_filters=32, filter_size=5, stride=1, padding=2, act='relu')
self.conv3 = layers.conv2d(
num_filters=64, filter_size=4, stride=1, padding=1, act='relu')
self.conv4 = layers.conv2d(
num_filters=64, filter_size=3, stride=1, padding=1, act='relu')
self.algo = algo
# 若采用Dueling算法,需要各加两层全连接层计算出As和V
if algo == 'Dueling':
self.fc1_adv = layers.fc(size=512, act='relu')
self.fc2_adv = layers.fc(size=act_dim)
self.fc1_val = layers.fc(size=512, act='relu')
self.fc2_val = layers.fc(size=1)
# 否则的话直接用全连接层计算结果
else:
self.fc1 = layers.fc(size=act_dim)
# 输入状态值obs,输出Q值(act_dim维)
def value(self, obs):
obs = obs / 255.0
out = self.conv1(obs)
out = layers.pool2d(
input=out, pool_size=2, pool_stride=2, pool_type='max')
out = self.conv2(out)
out = layers.pool2d(
input=out, pool_size=2, pool_stride=2, pool_type='max')
out = self.conv3(out)
out = layers.pool2d(
input=out, pool_size=2, pool_stride=2, pool_type='max')
out = self.conv4(out)
out = layers.flatten(out, axis=1)
if self.algo == 'Dueling':
As = self.fc2_adv(self.fc1_adv(out))
V = self.fc2_val(self.fc1_val(out))
# 下面这行代码若按论文里的公式写成Q = V + (As - layers.reduce_mean(As, dim=1, keep_dim=True))会更好理解
# 不过由于加法的性质不影响最终结果
Q = As + (V - layers.reduce_mean(As, dim=1, keep_dim=True))
else:
Q = self.fc1(out)
return Q
接着我们一起看下PARL中DQN和DDQN的算法层代码。可以看出两者都是在一开始利用深拷贝复制一个和主model一样的target_model,然后在训练时周期性地调用sync_target这个方法来同步参数。区别在于next_action的选择方式不同,DQN是通过target_model,而DDQN是通过主model得到,具体原因前文已经分析过了(为了降低overestimation)。
class DQN(Algorithm):
def __init__(self, model, act_dim=None, gamma=None, lr=None):
""" DQN algorithm
Args:
model (parl.Model): model defining forward network of Q function
act_dim (int): dimension of the action space
gamma (float): discounted factor for reward computation.
lr (float): learning rate.
"""
# 传入的model即为要学习的model,以下统称主model
self.model = model
# 在初始化的时候用深拷贝的方式复制一个和主model一模一样的target_model
self.target_model = copy.deepcopy(model)
assert isinstance(act_dim, int)
assert isinstance(gamma, float)
# 可选action的个数
self.act_dim = act_dim
# reward的衰减因子
self.gamma = gamma
# 学习率
self.lr = lr
# 输入obs,返回神经网络的输出结果(即Q值)
def predict(self, obs):
""" use value model self.model to predict the action value
"""
return self.model.value(obs)
def learn(self,
obs,
action,
reward,
next_obs,
terminal,
learning_rate=None):
""" update value model self.model with DQN algorithm
"""
# Support the modification of learning_rate
if learning_rate is None:
assert isinstance(
self.lr,
float), "Please set the learning rate of DQN in initializaion."
learning_rate = self.lr
# 当前状态下预测的Q值
pred_value = self.model.value(obs)
# 下一状态下预测的Q值
next_pred_value = self.target_model.value(next_obs)
# 取act_dim个Q值中最大的
best_v = layers.reduce_max(next_pred_value, dim=1)
# 阻止梯度传递
best_v.stop_gradient = True
# 用当前收益与一系列未来收益的和作为target值
target = reward + (
1.0 - layers.cast(terminal, dtype='float32')) * self.gamma * best_v
# 将action转为onehot向量,方便之后计算action对应的 Q(s,a)
action_onehot = layers.one_hot(action, self.act_dim)
action_onehot = layers.cast(action_onehot, dtype='float32')
pred_action_value = layers.reduce_sum(
layers.elementwise_mul(action_onehot, pred_value), dim=1)
# 计算MSE
cost = layers.square_error_cost(pred_action_value, target)
cost = layers.reduce_mean(cost)
# 用Adam优化器更新网络参数
optimizer = fluid.optimizer.Adam(
learning_rate=learning_rate, epsilon=1e-3)
optimizer.minimize(cost)
return cost
# 以主model为基准,同步target_model的参数
def sync_target(self):
""" sync weights of self.model to self.target_model
"""
self.model.sync_weights_to(self.target_model)
class DDQN(Algorithm):
def __init__(self, model, act_dim=None, gamma=None, lr=None):
""" Double DQN algorithm
Args:
model (parl.Model): model defining forward network of Q function
act_dim (int): dimension of the action space
gamma (float): discounted factor for reward computation.
lr (float): learning rate.
"""
self.model = model
self.target_model = copy.deepcopy(model)
assert isinstance(act_dim, int)
assert isinstance(gamma, float)
self.act_dim = act_dim
self.gamma = gamma
self.lr = lr
def predict(self, obs):
""" use value model self.model to predict the action value
"""
return self.model.value(obs)
def learn(self,
obs,
action,
reward,
next_obs,
terminal,
learning_rate=None):
""" update value model self.model with DQN algorithm
"""
# Support the modification of learning_rate
if learning_rate is None:
assert isinstance(
self.lr,
float), "Please set the learning rate of DQN in initializaion."
learning_rate = self.lr
pred_value = self.model.value(obs)
action_onehot = layers.one_hot(action, self.act_dim)
action_onehot = layers.cast(action_onehot, dtype='float32')
pred_action_value = layers.reduce_sum(
layers.elementwise_mul(action_onehot, pred_value), dim=1)
# choose acc. to behavior network
# 与DQN的区别就在于这里DDQN所选择的next_action是通过主model获得的
next_action_value = self.model.value(next_obs)
greedy_action = layers.argmax(next_action_value, axis=-1)
# calculate the target q value with target network
batch_size = layers.cast(layers.shape(greedy_action)[0], dtype='int64')
range_tmp = layers.range(
start=0, end=batch_size, step=1, dtype='int64') * self.act_dim
a_indices = range_tmp + greedy_action
a_indices = layers.cast(a_indices, dtype='int32')
next_pred_value = self.target_model.value(next_obs)
next_pred_value = layers.reshape(
next_pred_value, shape=[
-1,
])
# 取出greedy_action对应的Q值,这里的max_v就相当于DQN代码里的best_v
max_v = layers.gather(next_pred_value, a_indices)
max_v = layers.reshape(
max_v, shape=[
-1,
])
max_v.stop_gradient = True
target = reward + (
1.0 - layers.cast(terminal, dtype='float32')) * self.gamma * max_v
cost = layers.square_error_cost(pred_action_value, target)
cost = layers.reduce_mean(cost)
optimizer = fluid.optimizer.Adam(
learning_rate=learning_rate, epsilon=1e-3)
optimizer.minimize(cost)
return cost
def sync_target(self):
""" sync weights of self.model to self.target_model
"""
self.model.sync_weights_to(self.target_model)