07.5. 批量规范化

7.5. 批量规范化

批量规范化（batch normalization）]，这是一种流行且有效的技术，可持续加速深层网络的收敛速度.

7.5.1. 训练深层网络

为什么需要批量规范化层呢?

• 首先，数据预处理的方式通常会对最终结果产生巨大影响
• 对于典型的多层感知机或卷积神经网络
• 更深层的网络很复杂，容易过拟合。 这意味着正则化变得更加重要。

量规范化应用于单个可选层（也可以应用到所有层），其原理如下：
在每次训练迭代中，我们首先规范化输入，即通过减去其均值并除以其标准差，其中两者均基于当前小批量处理。
接下来，我们应用比例系数和比例偏移。
正是由于这个基于批量统计的标准化，才有了批量规范化的名称。

另外，批量规范化层在”训练模式“（通过小批量统计数据规范化）和“预测模式”（通过数据集统计规范化）中的功能不同。

• 在训练过程中，我们无法得知使用整个数据集来估计平均值和方差，所以只能根据每个小批次的平均值和方差不断训练模型。
• 而在预测模式下，可以根据整个数据集精确计算批量规范化所需的平均值和方差。

7.5.2. 批量规范化层

全连接层和卷积层，他们的批量规范化实现略有不同。

7.5.2.1. 全连接层

通常，我们将批量规范化层置于全连接层中的仿射变换和激活函数之间。

7.5.2.2. 卷积层

对于卷积层，我们可以在卷积层之后和非线性激活函数之前应用批量规范化。

7.5.2.3. 预测过程中的批量规范化

批量规范化在训练模式和预测模式下的行为通常不同。

• 首先，将训练好的模型用于预测时，我们不再需要样本均值中的噪声以及在微批次上估计每个小批次产生的样本方差了。 - 其次，例如，我们可能需要使用我们的模型对逐个样本进行预测。 一种常用的方法是通过移动平均估算整个训练数据集的样本均值和方差，并在预测时使用它们得到确定的输出。

7.5.3. 从零实现

下面，我们从头开始实现一个具有张量的批量规范化层。

import torch
from torch import nn
from d2l import torch as d2l


def batch_norm(X, gamma, beta, moving_mean, moving_var, eps, momentum):
    # 通过is_grad_enabled来判断当前模式是训练模式还是预测模式
    if not torch.is_grad_enabled():
        # 如果是在预测模式下，直接使用传入的移动平均所得的均值和方差
        X_hat = (X - moving_mean) / torch.sqrt(moving_var + eps)
    else:
        assert len(X.shape) in (2, 4)
        if len(X.shape) == 2:
            # 使用全连接层的情况，计算特征维上的均值和方差
            mean = X.mean(dim=0)
            var = ((X - mean) ** 2).mean(dim=0)
        else:
            # 使用二维卷积层的情况，计算通道维上（axis=1）的均值和方差。
            # 这里我们需要保持X的形状以便后面可以做广播运算
            mean = X.mean(dim=(0, 2, 3), keepdim=True)
            var = ((X - mean) ** 2).mean(dim=(0, 2, 3), keepdim=True)
        # 训练模式下，用当前的均值和方差做标准化
        X_hat = (X - mean) / torch.sqrt(var + eps)
        # 更新移动平均的均值和方差
        moving_mean = momentum * moving_mean + (1.0 - momentum) * mean
        moving_var = momentum * moving_var + (1.0 - momentum) * var
    Y = gamma * X_hat + beta  # 缩放和移位
    return Y, moving_mean.data, moving_var.data

通常情况下，我们用一个单独的函数定义其数学原理，比如说batch_norm。
然后，我们将此功能集成到一个自定义层中，其代码主要处理数据移动到训练设备（如GPU）、分配和初始化任何必需的变量、跟踪移动平均线（此处为均值和方差）等问题

class BatchNorm(nn.Module):
    # num_features：完全连接层的输出数量或卷积层的输出通道数。
    # num_dims：2表示完全连接层，4表示卷积层
    def __init__(self, num_features, num_dims):
        super().__init__()
        if num_dims == 2:
            shape = (1, num_features)
        else:
            shape = (1, num_features, 1, 1)
        # 参与求梯度和迭代的拉伸和偏移参数，分别初始化成1和0
        self.gamma = nn.Parameter(torch.ones(shape))
        self.beta = nn.Parameter(torch.zeros(shape))
        # 非模型参数的变量初始化为0和1
        self.moving_mean = torch.zeros(shape)
        self.moving_var = torch.ones(shape)

    def forward(self, X):
        # 如果X不在内存上，将moving_mean和moving_var
        # 复制到X所在显存上
        if self.moving_mean.device != X.device:
            self.moving_mean = self.moving_mean.to(X.device)
            self.moving_var = self.moving_var.to(X.device)
        # 保存更新过的moving_mean和moving_var
        Y, self.moving_mean, self.moving_var = batch_norm(
            X, self.gamma, self.beta, self.moving_mean,
            self.moving_var, eps=1e-5, momentum=0.9)
        return Y

7.5.4. 使用批量规范化层的 LeNet

为了更好理解如何应用BatchNorm，下面我们将其应用于LeNet模型（ 6.6节）。 回想一下，批量规范化是在卷积层或全连接层之后、相应的激活函数之前应用的。

net = nn.Sequential(
    nn.Conv2d(1, 6, kernel_size=5), BatchNorm(6, num_dims=4), nn.Sigmoid(),
    nn.AvgPool2d(kernel_size=2, stride=2),
    nn.Conv2d(6, 16, kernel_size=5), BatchNorm(16, num_dims=4), nn.Sigmoid(),
    nn.AvgPool2d(kernel_size=2, stride=2), nn.Flatten(),
    nn.Linear(16*4*4, 120), BatchNorm(120, num_dims=2), nn.Sigmoid(),
    nn.Linear(120, 84), BatchNorm(84, num_dims=2), nn.Sigmoid(),
    nn.Linear(84, 10))
    
# 在Fashion-MNIST数据集上训练网络
lr, num_epochs, batch_size = 1.0, 10, 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())

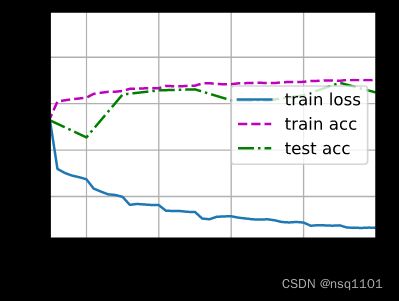
# result
loss 0.268, train acc 0.900, test acc 0.831
38739.6 examples/sec on cuda:0

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-EJzCn6HI-1665280421103)(https://zh.d2l.ai/_images/output_batch-norm_cf033c_42_1.svg)]

让我们来看看从第一个批量规范化层中学到的拉伸参数gamma和偏移参数beta。

net[1].gamma.reshape((-1,)), net[1].beta.reshape((-1,))

# result
(tensor([0.3362, 4.0349, 0.4496, 3.7056, 3.7774, 2.6762], device='cuda:0',
        grad_fn=),
 tensor([-0.5739,  4.1376,  0.5126,  0.3060, -2.5187,  0.3683], device='cuda:0',
        grad_fn=)

7.5.5. 简明实现

直接使用深度学习框架中定义的BatchNorm

net = nn.Sequential(
    nn.Conv2d(1, 6, kernel_size=5), nn.BatchNorm2d(6), nn.Sigmoid(),
    nn.AvgPool2d(kernel_size=2, stride=2),
    nn.Conv2d(6, 16, kernel_size=5), nn.BatchNorm2d(16), nn.Sigmoid(),
    nn.AvgPool2d(kernel_size=2, stride=2), nn.Flatten(),
    nn.Linear(256, 120), nn.BatchNorm1d(120), nn.Sigmoid(),
    nn.Linear(120, 84), nn.BatchNorm1d(84), nn.Sigmoid(),
    nn.Linear(84, 10))
    
d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())

# result
loss 0.269, train acc 0.901, test acc 0.853
64557.2 examples/sec on cuda:0

7.5.6 小结

• 在模型训练过程中，批量规范化利用小批量的均值和标准差，不断调整神经网络的中间输出，使整个神经网络各层的中间输出值更加稳定。

• 批量规范化在全连接层和卷积层的使用略有不同。

• 批量规范化层和暂退层一样，在训练模式和预测模式下计算不同。

• 批量规范化有许多有益的副作用，主要是正则化。另一方面，”减少内部协变量偏移“的原始动机似乎不是一个有效的解释