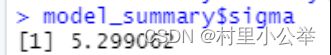R语言-线性回归实例(包括所有源码)
题目描述
目录
一、身高体重
1.身高和体重的散点图(先肉眼观察来判断使用什么模型)
2.画出拟合后的线性函数与散点图背景对比
3.对该模型的分析
4.置信区间分析和假设检验
5.多图像分析
二、不良贷款
三、污染
1.以二氧化硫排放量(吨)为因变量
2.氮氧化物排放量(吨)为因变量
编辑
3.烟(粉)尘排放量(吨)
一、身高体重
1.身高和体重的散点图(先肉眼观察来判断使用什么模型)
我们可以看到体重和身高大致还是呈现线性关系,尤其是在两端时候。但是由于我们的数据是男女混合,可能男生女生对于体重有不同的追求,进而导致数据拟合中间端看起来不是太线性。
# library
library(ggplot2)
# The iris dataset is provided natively by R
#head(iris)
data <- data.frame(
体重=c(63,71,80,68,56,63,65,70,63,55,80,70,70,60,55,47,55,47,68.5,55,75,65,65,66,56,60) ,
身高=c(180,178,181,172,178,170,170,190,179,170,185,178,170,179,164,162,170,168,186,175,178,178,178,181,167,180)
)
# basic scatterplot
ggplot(data, aes(x=体重, y=身高)) + 根据散点图,我们使用一元线性回归
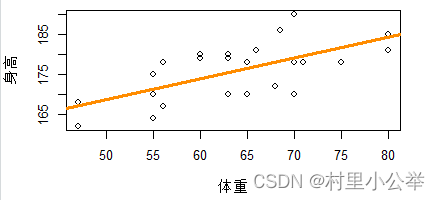
2.画出拟合后的线性函数与散点图背景对比
我们观察图像,发现该直线还是较为拟合,但是也有一些偏离度较大的点
library(gcookbook) #引用gcookbook数据集
heightweight<- data.frame(
体重=c(63,71,80,68,56,63,65,70,63,55,80,70,70,60,55,47,55,47,68.5,55,75,65,65,66,56,60) ,
身高=c(180,178,181,172,178,170,170,190,179,170,185,178,170,179,164,162,170,168,186,175,178,178,178,181,167,180)
) #heightweight为下面分析所用数据
summary(heightweight) #查看数据基本内容
model <- lm(身高 ~ 体重,data = heightweight) #建立回归模型 #直接查看回归系数
summary(model) #查看回归模型参数
plot(身高 ~ 体重,data = heightweight,xlab="体重",ylab = "身高")
abline(model,lwd=3,col="darkorange")3.对该模型的分析
参数总体分析
系数参数,可知两参数分别为142.8399344和0.5175382
残差分析
估计误差项标准差
拟合优度分析
我们发现R为0.4288243,其拟合的效果不是很好
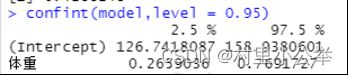
4.置信区间分析和假设检验
以0.05为置信度
假设检验
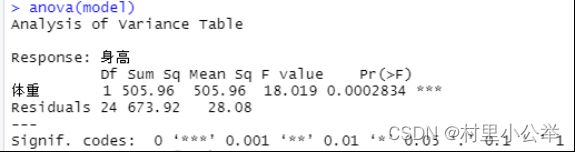
F检验
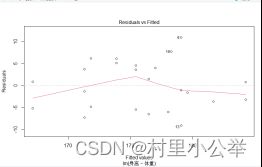
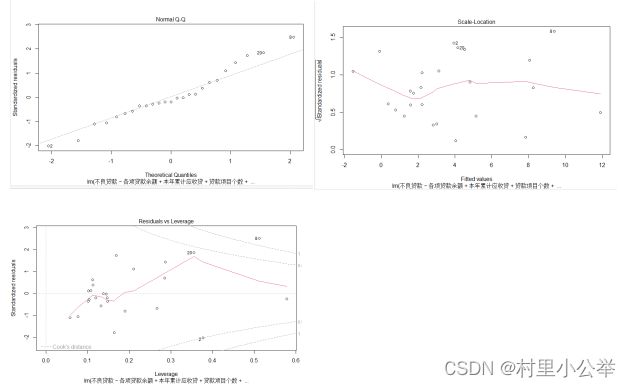
5.多图像分析
这就是残差与真实值之间的关系画图。在理想线性模型中有五大假设,其中之一便是残差应该是一个正态分布,与估计值无关(近乎是一条直线)。
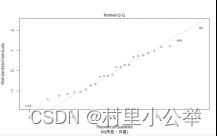
Normal QQ-plot用来检测其残差是否是正态分布的。根据图可以判断残差基本为正态分布
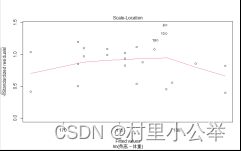
这个图是用来检查等方差假设的。可以看到这个直线基本水平,可以认为反差不变
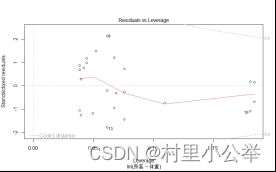
Leverage就是杠杆的意思。这种图的意义在于检查数据分析项目中是否有特别极端的点。
在这里我们引入了一个非常重要的指标:Cook距离。我们在线性模型里用Cook距离分析一个点是否非常“influential。”一般来说距离大于0.5的点就需要引起注意了。
我们可以看到极端的点有很多
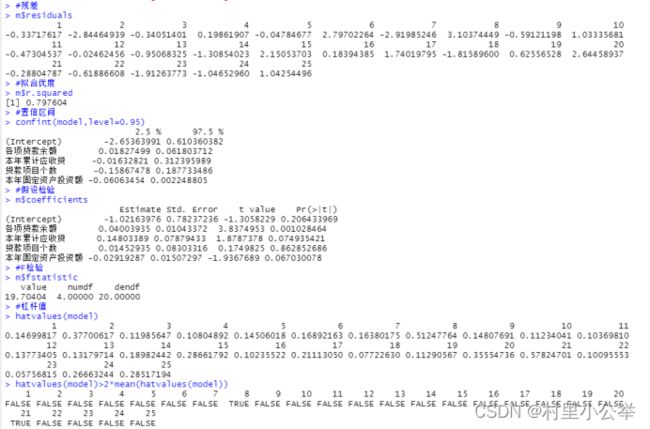
二、不良贷款
library(readxl)
datas = read_excel("D:/浏览器下载路径/loan.xls")
model = lm(不良贷款~各项贷款余额+本年累计应收贷 +贷款项目个数 +本年固定资产投资额,data=datas)
m=summary(model)
plot(model)
#拟合系数
coef(model)
#估计标准误
m$sigma
#残差
m$residuals
#拟合优度
m$r.squared
#置信区间
confint(model,level=0.95)
#假设检验
m$coefficients
#F检验
m$fstatistic
#杠杆值
hatvalues(model)
hatvalues(model)>2*mean(hatvalues(model))三、污染
library(readxl)
datas = read_excel("D:/浏览器下载路径/pollution.xlsx")
datas = na.omit(datas)
model = lm(SO2 ~ cabon+ ethene+ cement+ glass+ pigiron+ crudesteel+ steel+ capacity+ coal
,data=datas)
m=summary(model)
#拟合系数
coef(model)
#估计标准误
m$sigma
#残差
m$residuals
#拟合优度
m$r.squared
#置信区间
confint(model,level=0.95)
#假设检验
m$coefficients
#F检验
m$fstatistic
#杠杆值
hatvalues(model)
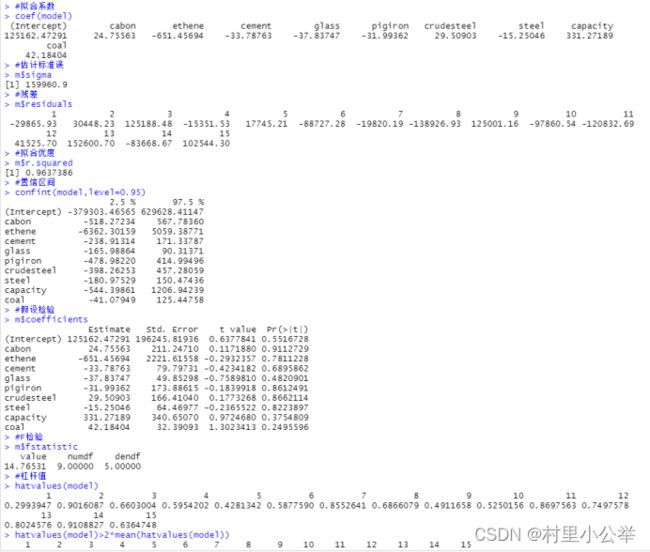
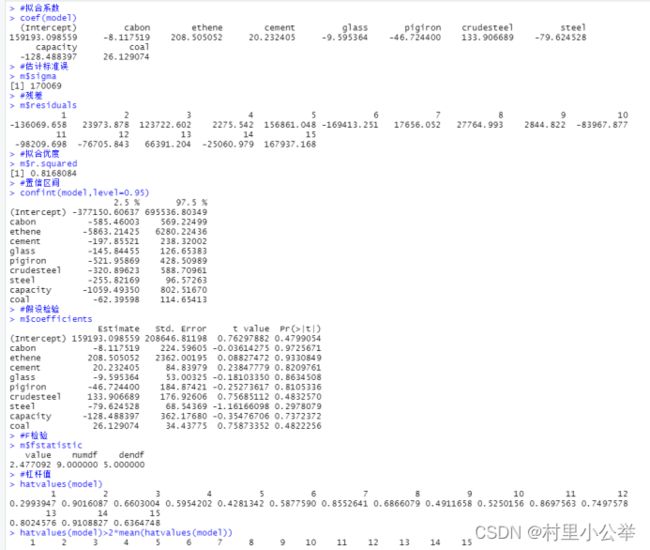
hatvalues(model)>2*mean(hatvalues(model))先做出相关系数的矩阵,我们发现三种排放量之间高度相关,乙烯产量与大部分不相关
1.以二氧化硫排放量(吨)为因变量
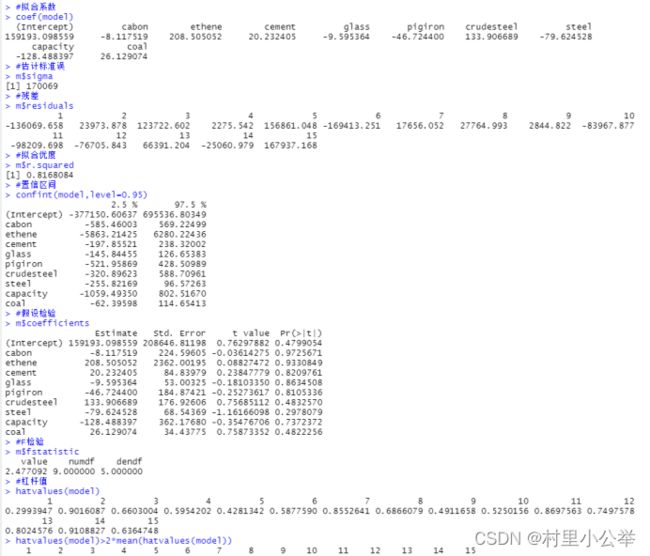
2.氮氧化物排放量(吨)为因变量
3.烟(粉)尘排放量(吨)
简单预测