MATLAB中果蝇味道浓度判定函数,果蝇优化算法的加权策略研究
摘 要: 针对基本果蝇优化算法(FOA)收敛速度慢和寻优精度不高的缺点,在位置更新公式中引入加权因子,提出了基于线性递减策略和先增后减策略的两种加权果蝇优化算法(WFOA),从而增强了种群的多样性。通过对6个测试函数的仿真实验,验证了这些策略的可行性,表明这些策略能够有效地提高算法的收敛速度和搜优精度。经过两种策略的对比,发现线性递减策略具有更快的收敛速度,而先增后减策略具有更强的鲁棒性和稍好的寻优精度。
关键词: 加权因子;果蝇优化算法;线性递减策略;先增后减策略
果蝇优化算法FOA(Fruit Fly Optimization Algorithm)是由台湾博士潘文超于2011年提出的,与蚁群算法和粒子群算法类似,是基于动物群体觅食行为演化出的一种寻求全局优化的新方法[1-3]。它不同于顺序执行的传统智能算法,而是以果蝇群体自组织性和并行性为基础,构造出的一种动物自治体模型。FOA有着算法简单、控制参数少、容易实现、且具有一定并行性等特点,因此在各领域得到广泛应用[4]。FOA可以优化神经网络参数,已成功应用于企业经营绩效评估、外贸出口预测、原油含水率预测等[3,5-6];FOA也可优化支持向量机模型,已成功应用于故障诊断、物流需求量预测等[7-8]。但由于FOA是较晚提出的一种随机搜索算法,其在理论分析和应用研究等方面还处于初级阶段,同时也存在易发散、收敛精度不高等缺点。
本文针对FOA收敛速度慢、收敛精度低等缺点,提出了加权果蝇优化算法WFOA(Weighted Fruit Fly Optimization Algorithm),进而对几种不同加权策略下的果蝇优化算法进行了对比研究。
1 果蝇优化算法及其改进
1.1 果蝇优化算法
FOA在计算方法上类似于遗传算法,但不同的是FOA不使用杂交和变异等算子,而是通过模仿果蝇特殊的嗅觉和视觉特点来进行搜索。果蝇的嗅觉器官能很好地搜集飘浮在空气中的各种气味,甚至能嗅到几十公里以外的食物源。然后飞近食物位置,使用敏锐的视觉发现食物与同伴聚集的位置,并且往该方向飞去[2]。
根据果蝇搜索食物的特性,将果蝇优化算法归纳为以下几个必要的步骤[1-3]:
(1)给定群体规模Sizepop,最大迭代次数Maxgen,随机初始化果蝇群体位置X_axis,Y_axis;
(2)赋予果蝇个体利用嗅觉搜寻食物的方向与距离:
Xi=X_axis+Random ValueYi=Y_axis+Random Value(1)
(3)由于无法得知食物位置,因此先估计与原点的距离Disti,再计算味道浓度判定值Si,此值为距离的倒数:
![]()
Si=1/Disti(3)
(4)将味道浓度判定值代入味道浓度判定函数(或称为适应度函数Fitness Function),以求出果蝇个体的味道浓度Smelli:
Smelli=Function(Si)(4)
(5)找出该果蝇群体中味道浓度最佳的果蝇(求极小值):
[bestSmell bestindex]=min(Smelli)(5)
(6)记录并保留最佳味道浓度值bestSmell与其X、Y坐标,此时果蝇群体利用视觉向该位置(Fly2)飞去,形成新的群聚位置:
Smellbest=bestSmellX_axis=X(bestindex)Y_axis=Y(bestindex)(6)
(7)进入迭代寻优,重复执行步骤(2)~步骤(5),并判断最佳味道浓度是否优于前一迭代最佳味道浓度,前提是当前迭代次数小于等于Maxgen,若是则执行步骤(6)。
1.2 加权果蝇优化算法(WFOA)
在FOA中,每个果蝇个体在n维搜索空间中通过适应度函数来衡量个体的优劣,当种群完成一次迭代后,与群体的历史最佳位置比较得出新的最佳位置,进而在新最佳位置附近继续随机寻优。由式(1)可以看出,迭代搜索始终在以当前最优位置为中心,以随机飞行方向与距离Random Value为半径的领域内展开,果蝇群体被限定在过分狭小的搜索范围内,降低了种群的多样性[9]。受PSO(粒子群算法)的惯性权重启发[10-11],在迭代位置更新公式中引入加权因子w,将式(1)变更如下,其他步骤不变。
Xi=w×X_axis+Random ValueYi=w×Y_axis+Random Value(7)
在迭代寻优过程中,希望前期具有较强的“探索”能力,即较强的全局搜索能力,以得到合适的种子,而在迭代后期,应具有较强的“开发”能力,即较强的局部搜索能力,从而展开精细的局部搜索。前期具有较大的值,一方面是对自己“历史经验”的认可,能够充分利用果蝇个体本身的历史记忆;另一方面使得个体搜索的区域范围变大,让果蝇个体在更广的可行域里进行搜索,整个群体找到最优解的概率就大,相应的全局搜索能力就强。随着迭代进行到后期,需要较小的w值,使其可搜索的范围相对缩小,这时主要根据随机飞行方向与距离Random Value,在“以往经验”寻到的最优解附近进行小范围精细搜索。
1.3 加权因子的几种调整策略
策略1 线性递减
w1=Wmax-(Wmax-Wmin)/Maxgen×g(8)
策略2 先增后减
令d=g/Maxgen,则有:
w2=d+1, 0≤d≤0.4w2=-7/6×d+28/15,0.4≤d≤1(9)
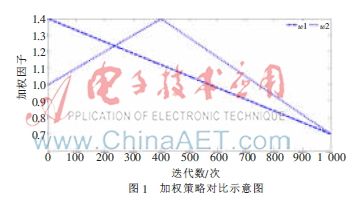
其中,g为当前迭代数,Maxgen为最大迭代数,Wmax为最大加权因子,Wmin为最小加权因子。对于策略1,经过实验仿真,分别确定Wmax、Wmin为1.4、0.7的最佳权值范围,随着迭代数的变化,权值从1.4线性递减到0.7,具体参数设置见式(8)。对于策略2,从第一次迭代开始到第Maxgen的40%代,权值从1线性递增到1.4,而从Maxgen的40%代直至迭代结束,权值从1.4线性递减到0.7,具体参数设置见式(9),两种策略随迭代的权值变化如图1所示。
由式(8)和图1可看出,策略1在进化初期具有很强的全局搜索能力。如果在初期能搜索到最好点,可在迭代前期达到快速收敛。由式(9)和图1可看出,策略2在迭代开始至Maxgen的40%期间,全局搜索能力逐渐增强,而从Maxgen的40%到结束期间,其全局搜索能力逐渐减弱。由此可知,在没有陷入局部极值的情况下,策略1比策略2应该具有更快的收敛速度。
2 实验仿真及结果分析
2.1 实验设计
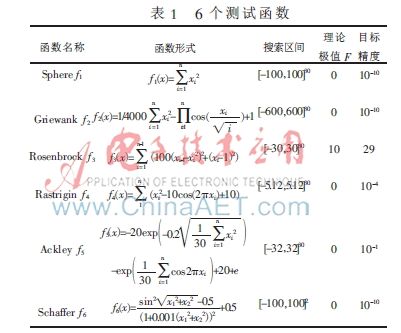
为了测试w0-FOA、w1-FOA、w2-FOA算法的寻优性能,本文选用6个常用于优化算法比较的基准函数,函数形式、搜索区间、理论极值和目标精度如表1所示[4]。其中w0-FOA是w取固定值1,即基本FOA算法。具体参数设置为:群体规模Sizepop=30,最大迭代数Maxgen=1 000;随机初始化果蝇群体位置为表1中各函数的搜索区间;迭代的果蝇搜寻食物的随机飞行方向与距离区间为[-1,1]。测试软件平台为Windows7、MATLAB 2012b,机器主频为2.5 GHz,内存为2 GB。
2.2 实验结果与分析
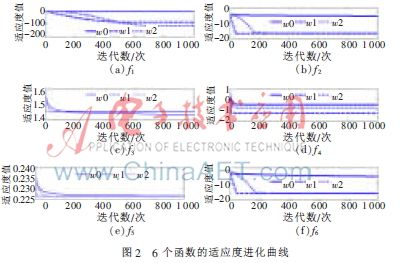
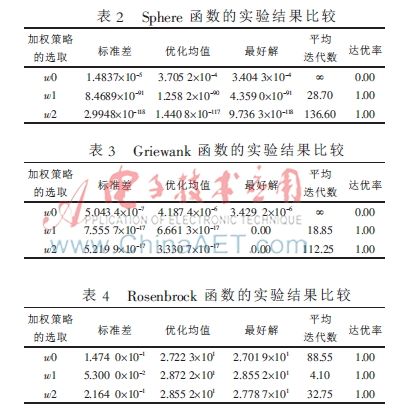
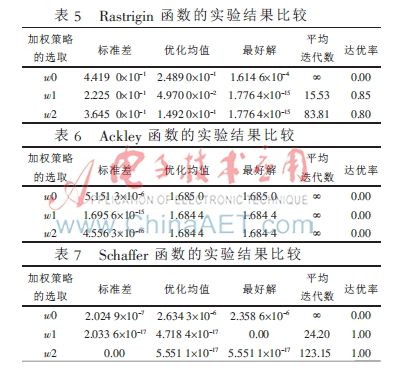
6个测试函数在固定迭代数为1 000次,分别采用w0-FOA、w1-FOA和w2-FOA经过20次独立运行后的标准差、优化均值和最好解如表2~表7所示;6个测试函数在表1中指定的目标精度下经过20次独立运行后的平均迭代次数和达优率亦见表2~表7。其中,平均迭代数是达到目标精度的迭代数平均值,达优率为达到目标精度的运行次数与总实验次数之比。图2是6个测试函数适应度对数值进化曲线(注:为了方便进化曲线的显示和观察,本文对函数的适应度取以10为底的对数)。
从表2、3、7可以看出,w0-FOA对f1、f2、f6未能达到目标精度,而w1-FOA和w2-FOA都能100%达到目标精度,并且改进算法的收敛精度与w0-FOA的收敛精度相差11个数量级以上。从表6可以看出,虽然3种策略对f5均未达到指定的目标精度,但是w1-FOA和w2-FOA找到的最好解要比w0-FOA找到的优。而从表5可以看出,w1-FOA的均值和鲁棒性是其中最好的,w2-FOA和w0-FOA的优化均值相差不大,但是w2-FOA找到的最好解要比w0-FOA找到的最好解优11个数量级。其中效果不太好的是f3函数,因为此函数的全局最优点隐藏在一条狭长的通道中,对外提供很少的信息,使算法很难辨别搜索方向,WFOA的优势体现不出。
由图2和表2~表7可看出,w1-FOA最多只需28.70次迭代就能达到目标精度(除f5),w2-FOA也最多只需136.60次迭代就可达到目标精度(除f5),由此可见,WFOA对收敛速度的影响非常显著。
本文提出的WFOA算法在引入加权因子的基础上,对粒子群算法中的线性递减策略和先增后减策略公式进行了适当的参数调整,经测试函数验证发现,总体上改进算法比原算法具有更快的收敛速度和更好的收敛精度,但w1-FOA比w2-FOA具有更快的收敛速度,而w2-FOA具有更强的鲁棒性和稍好的寻优精度。值得注意的是,不同加权策略对收敛速度的影响非常明显,如何正确选择权值策略和适当参数,使收敛速度和收敛精度达到最佳平衡,是接下来需要研究的问题。
参考文献
[1] PAN W T. A new fruit fly optimization algorithm: taking the financial distress model as an example[J]. Knowledge-based Systems, 2012,26:69-74.
[2] 潘文超.果蝇最佳化演算法[M].台北:沧海书局,2011.
[3] 潘文超.应用果蝇优化算法优化广义回归神经网络进行企业经营绩效评估[J].太原理工大学学报(社会科学版),2011,29(4):1-5.
[4] 韩俊英,刘成忠.基于细菌趋化的果蝇优化算法[J].计算机应用,2013,33(4):964-966.
[5] 许智慧,王福林,孙丹丹,等.基于FOA_RBF神经网络的外贸出口预测[J].数学的实践与认识,2012,42(13):14-19.
[6] 刘翠玲,张路路,王进旗,等.基于FOA—GRNN油井计量原油含水率的预测[J].计算机仿真,2012,29(11):243-246.
[7] 张翔,陈林.基于果蝇优化算法的支持向量机故障诊断[J].电子设计工程,2013,21(16):90-93.
[8] 李泓泽,郭森,李春杰.果蝇优化最小二乘支持向量机混合预测模型[J].经济数学,2012,29(3):103-106.
[9] 潘峰,李位星,高琪,等.粒子群优化算法与多目标优化[M].北京:北京理工大学出版社,2013.
[10] SHI Y, EBERHART R. Empirical study of particle swarm optimization[C]. International Conference on Evolutionary,Washington: USA,1999:1945-1950.
[11] 崔红梅,朱庆保.微粒群算法的参数选择及收敛性分析[J].计算机工程与应用,2007,43(23):89-91.