数据结构之线索二叉树详细解释
1.1 线索二叉树的原理
我们现在倡导节约型社会,一切都应该以节约为本。但当我们创建二叉树时我们会发现其中一共有两个指针域,有的指针域指向的结构为空,这也就浪费了很多空间。所以为了不去浪费这些空间我们采取了一个措施。就是利用那些空地址,存放指向结点在某种遍历次序之下 的前驱和后继结点的地址。就好像GPS导航仪一样,它可以告诉我们下一站是哪里,我们是从那里来的。我们把这种指向前驱和后继的指针成为线索,加上线索的二叉链表称为线索链表,相应的二叉树就成为线索二叉树。
我们将对二叉树以某种次序遍历使其变为线索二叉树的过程称为线索化 。
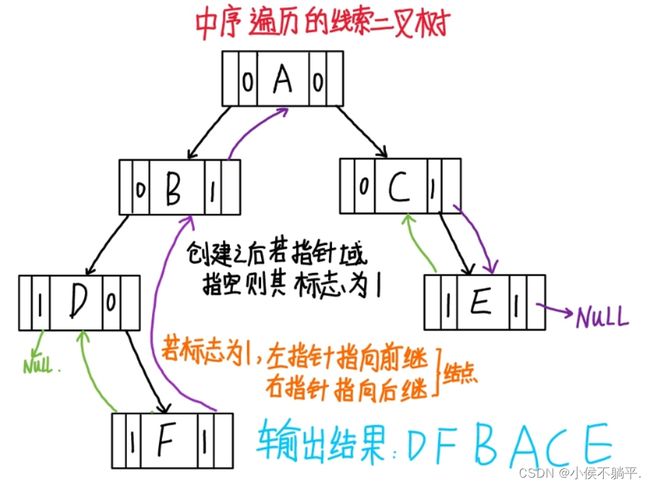
下图是线索化结束的图:
这里存在一个问题,我们怎么 知道某一个结点的lchild是指向它的左孩子还是它的前驱呢?rchild是指向其右孩子还是指向后继结点呢?可以在结构体中多两个变量用来去判断是指向前驱后继还是左孩子右孩子。
1.2 线索二叉树结构的实现
二叉树结构体线索存储结构如下:
struct Tree
{
char name[28]; //需要存储的数据
int num;
int L; //左右的标志
int R;
struct Tree *lchild,*rchild; //左右孩子的指针
};线索化的实质就是将二叉链表中的空指针改为指向前驱或后继的线索。由于前驱和后继的信息只有在遍历该二叉树的时候才能得到,所以线索化的过程就是在遍历的过程中修改空指针的过程。
中序遍历线索化的递归函数如下:
struct Tree *pre = NULL; //全局变量
void Inthreading(struct Tree *p)
{
Inthreading(p->lchild); //递归左子树线索化
if(!p->lchild) //没有左孩子
{
p->L = 1;
p->lchild = pre; //本来指向左孩子的指针指向前驱结点
}
if(!pre->rchild) //没有右孩子
{
pre->R = 1;
pre->rchild = p; //本来指向右孩子的指针指向后继结点
}
pre = p; //保持pre指向p的前驱
Inthreading(p->rchild); //递归右子树线索化
}你会发现,代码中除了if语句以外,和二叉树中序遍历的递归代码几乎一模一样。只不过是将打印的代码改为了线索化功能的代码。
if(!p->lchild)表示如果某结点的左指针域为空,因为其前驱结点刚刚访问过(如果是第一个元素则前驱指向NULL),赋值给了 pre,所以可以将pre赋值给p->lchild,并修改p->L为1,以完成前驱结点的线索化。
后继结点的线索化就会麻烦一点。因为此时p结点的后继结点还没有被访问到,因此只能对它的前驱结点pre的右指针rchild做判断,if(!pre->rchild)表示如果为空,则p就为pre的后继结点,于是就让pre->rchild = p,并设置pre->R为1,以完成后继结点的线索化。
结果如下图所示:
结构体中有一个标志(L和R)该指针域是否指向其左孩子还是右孩子的结点,若指向左孩子或右孩子则该值为0,若指向前驱或后继时则该值为1。
遍历的代码如下:
void print(struct Tree *T)
{
struct Tree *p;
p = T->lchid; //p指向根结点
while(p!=T) //当p是空树,或等于T时结束循环
{
while(p->L == 0)
p = p->lchild;
cout << name <<" " << num << endl;
while(p->R == 1 && p->rchild != T)
{
p = p->rchild; //访问后续结点
cout << name <<" " << num << endl;
}
p = p->rchild;
}
}大致运行的过程如下:
从此段代码也可以看出,它等于是一个链表的扫描,所以时间复杂度是O(n)。
由于它充分利用了空指针域的空间(这等于节省了空间),又保证了创建时的一次遍历就可以 终生享用前驱后继的信息(这意味着节省了时间)。所以在实际问题中,如果所用的二叉树经常要遍历或查找结点时需要某种遍历序列中的前驱后继,那么采用线索二叉链表的存储结构就是非常不错的选择。
1.3 树、森林与二叉树的转换
首先在介绍树、森林与二叉树转换之前我们先了解一下什么是树和森林吧。
树(tree)是n(n>=0)个结点的有限集。n=0时称为空树。在任意一颗非空树中:(1)有且仅有一个特定的称为根(boot)的结点;(2)当n>1时,其余结点可分为m(m>0)个互不相交的有限集T1、T2.....,其中每一个集合本身又是一颗树,并且称为根的树,如下图所示:
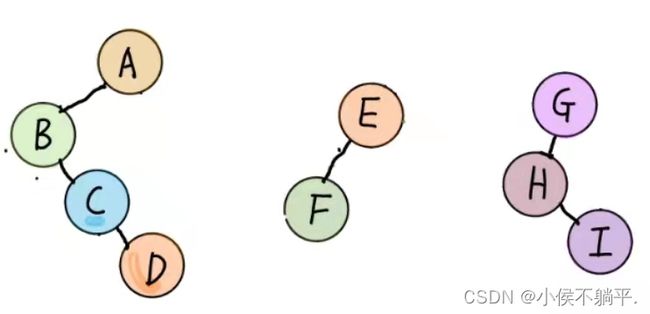
森林就是树和二叉树的一个集合,下图就是一个森林:
1.3.1 树转换为二叉树
树如下图所示:
将树转换为二叉树的步骤如下。
(1)加线。在所有兄弟节点之间加一条线,如下图所示:(树的话b的结点可以是三个,考虑画图过程本人没画很多 )
(2)去线。对树的每个结点,只保留它与第一个孩子结点的连线(即左孩子),删除它与其他孩子结点的连线。如下图所示:(树的话b的结点可以是三个,考虑画图过程本人没画很多 )
(3)层次调整。以树的根结点为轴心,将整棵树旋转一定的角度,使其结构层次分明。注意第一个孩子是二叉树的左孩子,兄弟转过来的孩子是结点的右孩子,如图所示:
1.3.2 森林转换为二叉树
森林是由若干颗树组成的,所以完全可以理解为,森林中的每一棵树都是兄弟,可以按照兄弟的处理办法来操作。如下图:
转换步骤如下:
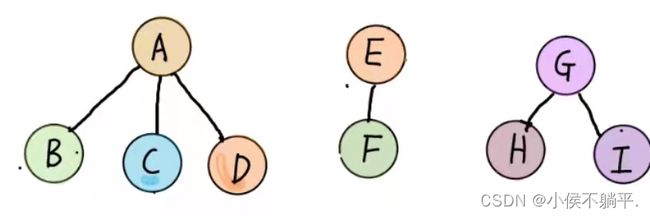
(1) 把每个树转换为二叉树,将根结点的右孩子断开作为下个结点的右孩子。如图所示:
(2)第一颗二叉树不动,从第二颗二叉树开始,一次把后一颗二叉树的根结点作为前一颗二叉树的根结点的右孩子,用连线连接起来。当所有的二叉树连接起来之后就得到了由森林转换过来的二叉树了。如下图所示:
1.3.3 二叉树转换为树
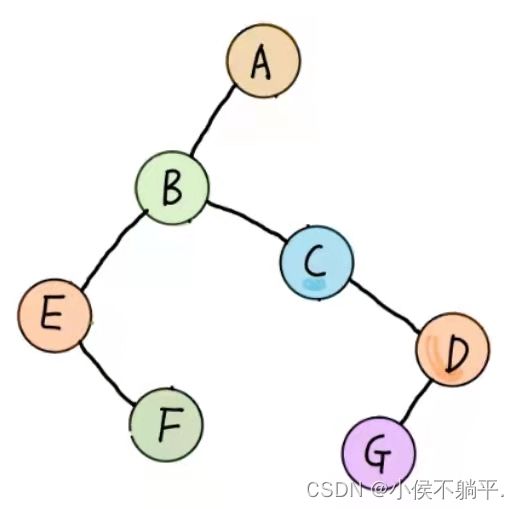
二叉树转换为树就是树转换为二叉树的逆过程,也就是反过来做而已。比如下图的二叉树转换为树 :
步骤如下:
(1)加线。如果结点的左孩子结点存在,则将这个左孩子的右孩子结点、右孩子的右孩子结点....与根部的结点相连接起来。如下图所示:(根据下图将右孩子都与根结点连接起来)
(2)去线。删除原二叉树中所有的结点与其右孩子结点的连线,如下图所示:
(3)层次调整。使其结构层次分明即可,如下图所示:
1.3.4 二叉树转换为森林
判断一颗二叉树能够转换成一颗树还是森林,标准很简单,就是只要看这颗二叉树的根结点有没有右孩子,有右孩子就是森林,没有就是一颗树。
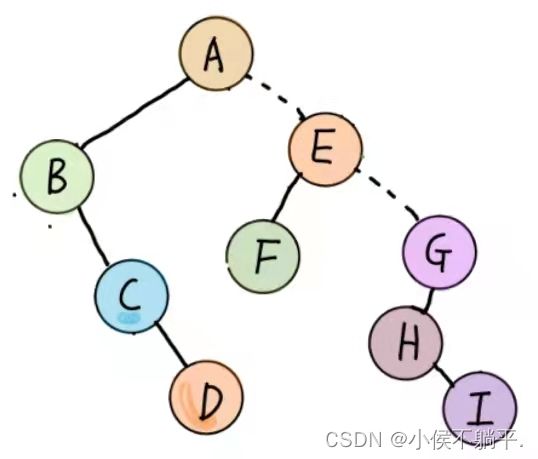
如下图:
步骤如下:
(1)从根结点开始,若右孩子存在,则把与右孩子所有的连线删除,如下图所示:
(2)再查看分离后的二叉树,若存在右孩子则连线继续删除,删除到没有右孩子的存在,得到分离的二叉树。如下图所示:
(3)再将每颗分离后的二叉树转换为树即可。如下图所示:
1.4 树与森林的遍历
树的遍历分为两种方式。
(1)先根遍历树。即先访问树的根结点,然后依次先根遍历根的每颗子树。
(2)后根遍历树。即先依次后根遍历每颗子树,然后再访问根结点。
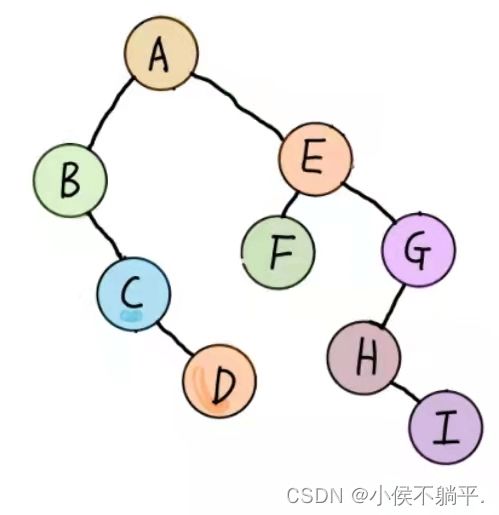
如下图:
先根遍历结果是:ABEFCGDHI
后根遍历结果是:EFBGCHIDA
森林的遍历也分为两种方式:
(1)前序遍历:先访问森林中的第一课树的根结点,然后再依次先根遍历根的每颗子树,在依次利用相同的方式遍历除去第一颗树的剩余树构成的森林。
(2)后序遍历:先访问森林中的第一颗树,后根遍历的方式遍历每一颗树,然后在访问根结点即可。
前序遍历结果是:ABCDEFGHI
后续遍历结果是:BCDAFEHIG
本篇博客的知识点就到这里结束了 ,后面博客再详细写一些程序作为应用介绍,因为放假回家没拿电脑,所以代码就没办法给大家实现了,先看看知识点进行复习吧!!