知识图谱顶会论文(SIGIR-2022) MorsE：归纳知识图嵌入的元知识迁移

MorsE：归纳知识图嵌入的元知识迁移

论文题目: Meta-Knowledge Transfer for Inductive Knowledge Graph Embedding
论文地址: https://scholar.archive.org/work/soegy2qe5jbbxbzdwrpgjvmhba/access/wayback/https://dl.acm.org/doi/pdf/10.1145/3477495.3531757
论文会议: ACM SIGIR 2022

目录

• 13.(2022.5.6)SIGIR-MorsE：归纳知识图嵌入的元知识迁移
  • 摘要
  • 1.引言
  • 2.相关工作
    • 2.1 知识图嵌入(KGE)
    • 2.2 归纳设置中的知识图谱
    • 2.3 元学习
  • 3.问题表述
  • 4.模型方法
    • 4.1 元知识建模
      • 4.1.1 实体初始化器
      • 4.1.2 GNN调制器
      • 4.1.3 总结
    • 4.2 元知识学习
      • 4.2.1 元学习设置
      • 4.2.2 元训练机制
    • 4.3 元知识自适应
      • 4.3.1 冻结模式
      • 4.3.2 微调模式

摘要

由大量三元组组成的知识图(KG)近年来得到了广泛的应用，人们提出了许多知识图嵌入(KGE)的方法来将KG的实体和关系嵌入到连续的向量空间中。这种嵌入方法简化了执行各种KG内任务(例如，链接预测)和KG外任务(例如，问题回答)的操作。它们可以被视为表达KG的通用方案。

然而，现有的KGE方法不适用于归纳设置，因为在归纳设置中，源KG上训练的模型将在模型训练时看不到的实体的目标KG上进行测试。

已有的研究主要集中在归纳设置下的知识发现上，只能解决归纳关系预测问题。这些归纳设置下的知识发现方法不能像KGE方法那样处理其他KG外任务，因为它们不为实体生成嵌入。

在本研究中，为了实现归纳知识图的嵌入，我们提出了一个MorsE模型，该模型不学习实体的嵌入，而是学习可转移的元知识，这些元知识可以用来产生实体嵌入。这种元知识由独立于实体的模块来建模，并通过元学习来学习。实验结果表明，在归纳设置下，我们的模型显著优于相应的KG内和KG外任务的基准模型。

简单来说，原有KGE不能用在归纳设置上，原有归纳方法也不能像KGE方法那样处理其他KG外任务，因此提出MorsE模型，使得可以在归纳设置上用于KG内外任务。

1.引言

知识图(KG)由大量的事实组成，如(头实体、关系实体、尾实体)的三元组形式，并且最近受益于许多下游任务。目前，已经提出了许多大规模的知识图，包括Freebase、Nell和Wikidata，并且已经支持许多KG内应用，例如链接预测和三元组分类；以及KG外应用，例如问答和推荐系统。

在将知识图应用于各种应用中时，很难直接使用离散结构的三元组(三元组元素往往是不能连续取值的文字)，因为现代深度学习方法不能容易地处理这种表示。因此，最近的许多工作将知识图的实体和关系嵌入到连续向量空间中，如TransE、ComplEx和RotatE。知识图的嵌入学习(即向量表示)可用于KG内任务，以提高KG内任务的质量；以及KG外任务，以帮助注入背景知识，例如实体之间的相似性和关系信息。

然而，在传统的KGE方法中，由于它们学习固定的预定义实体集的嵌入，因此仅能确保对在训练期间看到的实体而不是对于看不到的实体的有好的预测和应用。因此，对于KGE方法来说，在测试时出现新实体的归纳设置比直推设置(测试实体集包含在训练实体集中)更具挑战性。例如，如图1所示，在源KG上训练的KGE模型不能在目标KG上使用，因为在对源KG进行模型训练时看不到目标KG中的实体。

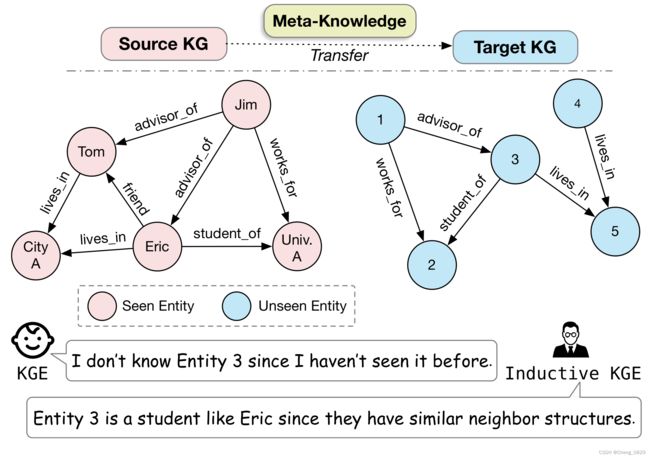
图1：归纳设置中的KG示例。传统的KGE方法就像一个只能识别可见实体的婴儿，而归纳KGE可以通过可转移的结构模式识别不可见的实体。

最近，在KG的归纳设置方面取得了重大进展，特别是在KG内任务中。具体地说，Grail及其后续工作进行了归纳关系预测，他们通过从候选关系周围的子图结构中学习预测关系来解决这个问题，避免学习对任何特定实体的嵌入。虽然这些方法被证明适合于归纳关系预测任务，但由于它们不产生实体的嵌入，因此不能解决其他KG外的任务。这一缺陷使得这种方法不像KGE方法那样通用地解决与KG相关的各种任务。为了解决归纳环境中KG的各种任务，我们提出了一个研究问题：“我们是否可以在一组实体上训练一个KGE模型，该模型可以泛化应用到KG内任务或KG外任务中的不可见实体？”我们将这个问题称为归纳知识图嵌入问题。

简单来说，原有KGE不能用在归纳设置上，原有归纳方法也不能像KGE方法那样处理其他KG外任务，因此提出MorsE模型，使得可以在归纳设置上用于KG内外任务。

为了解决这个问题，我们求助于人类认知的过程。如图1所示，传统的KGE方法就像一个婴儿，只能认知他们所看到的实体。相比之下，成年人可以通过比较邻居的结构模式和看到的实体来认知一个新的实体。这种帮助人类理解新实体的语义的结构模式是通用的、独立于实体的，并且是可转移的。在本文中，我们将关于这种可转移结构模式的知识统称为元知识。正是建模和学习这种元知识的能力，使得成人和模型能够成功地在归纳环境中处理KG。

受此启发，本文提出了一种新的归纳KGE元知识转移模型(MORSE)，该模型通过建模和学习与实体无关的元知识，为归纳环境中的新实体生成高质量的嵌入。

---

1. 对于元知识建模，我们重点对从实体无关信息中产生实体嵌入的过程进行建模。具体地说，我们将元知识实例化为两个模块，一个实体初始化器和一个图神经网络(GNN) 调制器。

   1. 实体初始化器通过两个实体无关的嵌入(关系域嵌入和关系范围嵌入)来初始化每个实体嵌入。
   2. GNN调制器基于实体的邻居结构信息来增强实体嵌入，使其从类型级别提升到实例级别。

   总体而言，这两个模块的参数独立于任何特定实体，并且可以在模型训练后适应于具有不可见实体的KG。

   具有相似连接关系和多跳邻域的实体将通过这两个模块获得相似的嵌入。因此，它们能够捕捉到KG中可转移的结构模式。

   ---

2. 对于元知识学习，我们借助于元学习来实现模型学习，从而产生实体嵌入。

   1. 在元训练机制下，在模型训练期间，我们在源KG上对一组任务进行采样，其中每个任务都由一个支持(三元组)集合和一个查询(三元组)集合组成。此外，这些任务中的实体被视为不可见，以模拟KG的归纳设置。
   2. 对于每个任务，实体嵌入由实体初始化器和GNN调制器基于支持集合产生，并在查询集合上进行评估。我们在源KG上对这些采样任务进行元训练MorsE，以强制它在给定任务的支持三元组的情况下产生合理有效的嵌入。因此，MorsE可以推广到具有看不见实体的目标KG。

---

我们通过对KG内任务(即链接预测)和KG外任务(即问题回答)的归纳设置来评估MorsE。结果表明，该模型的性能优于其他基准模型，能够有效地实现归纳知识图嵌入的元知识转移。本文的主要贡献概括如下：

• 我们强调将KGE作为表示KG内和KG外任务的通用解决方案，并将其扩展到归纳设置。
• 我们提出了一种通用的基于元知识转移的归纳KGE框架–MorsE，并通过元学习来学习此类元知识。
• 我们在归纳设置下KG内和KG外任务进行了大量的实验，证明了该模型的有效性。

2.相关工作

2.1 知识图嵌入(KGE)

KGE学习实体和关系的嵌入，同时保留KG的固有语义。这样的嵌入可以缓解将KG表示为离散结构化三元组的缺点，并且可以容易地部署到许多KG内任务，包括链接预测和三元组分类；以及KG外任务，包括问题回答和推荐系统。此外，KGE方法还在各种场景中进行了研究，如知识提取和联邦学习。

基于关系模式的一些特定假设，KGE的大部分工作集中于设计具有表现力的得分函数来对KG中的三元组建模。平移距离模型用关系进行平移后的尾部实体嵌入和头部实体嵌入之间的距离来衡量三元组的合理性。TransE是一个典型的平移距离模型，它将实体和关系表示为同一空间中的向量，并假设关系是实体之间的平移向量。最近，RotatE将每个关系视为复向量空间中从头实体到尾实体的旋转。此外，语义匹配模型通过匹配实体和关系的潜在语义来设计评分函数。DistMult通过捕获沿相同维度的实体组件之间的成对交互来获得三元组的得分。ComplEx遵循DistMult，但将KG的组件作为复数值嵌入来建模非对称关系。

最近，R-GCN和CompGCN等工作将通常用于简单无向图的GNN改为多关系知识图，以学习更具表现力的知识图嵌入。GNN可以看作是实体的编码器模型，它基于实体的多跳邻居结构将实体的特征编码到它们的嵌入中。GNN偏向于图对称，并被证明在捕获通用和一般结构模式方面是有效的，这可以更好地编码把传统KGE方法作为解码器的知识图嵌入。

虽然许多KGE方法已经被提出并被证明可以有效使用复杂的得分函数或GNNs处理各种关系模式，但它们是为直推设置中的KG相关任务设计的。也就是说，传统的KGE方法不能处理与训练期间看不见的实体有关的任务。

2.2 归纳设置中的知识图谱

知识图的归纳设置是一个更现实的场景，因为知识图在不停进化，每天都在使用新的实体构建新的知识图谱。有许多方法用来解决KG的归纳设置的不同问题。

基于规则学习的方法学习概率逻辑规则，这些规则可以用于对具有不可见实体的KG进行归纳推理。具体地说，AMIE和RuleN通过离散搜索明确地学习逻辑规则。Neural LP和DRUM以端到端可微的方式提取规则。由于规则与特定实体无关，因此基于规则学习的方法可以处理不可见实体的链接预测。

此外，一些方法求助于实体的附加信息，如用文本描述作为未知实体的表示。KG-BERT和StAR使用PLM对每个实体的文本描述进行编码。这些方法本质上是归纳的，因为只要它们有相应的描述，它们可以为任何未知实体生成嵌入。
但是，与其相比，我们的模型没有未知实体的任何特征或文本信息。在我们的工作中，实体嵌入完全基于KG结构，这是一个更通用的场景，可以适应各种应用。

其他一些工作侧重于处理与训练的KG有关的KG外实体。有的方法训练邻域聚集器以通过其现有邻居嵌入新实体。GEN和HRFN学习基于元学习的从已知到未知和从未知到未知的链接预测的实体嵌入。然而，它们都不能解决我们的论文的场景，即聚焦于在归纳环境中处理全新KG中的未知的实体。

简单来说，其他的方法都只是部分未知，而我们的模型能处理完全未知的实体。

对于我们的论文来说，最相关的工作是关于归纳式KGC的那些工作。这样的工作可以推广到看不见的实体，并对有全新实体的KG中的关系进行预测。具体地说，GraIL、CoMPILE和TACT通过与任何特定实体无关的的子图提取和GNN来学习关系预测的能力。这种能力可以推广到全新KG中看不见的实体。最近，INDIGO提出使用成对编码来实现基于GNN的归纳式KGC。虽然这些方法适合于归纳式KGC任务，但它们不能像我们的模型那样在归纳设置下处理其他KG外的任务。

其他的归纳式KGC模型都只能在KG内的任务中推广到全新KG，而我们的模型可以在KG外

2.3 元学习

元学习方法以“学会如何学习”的理念致力于培养能够快速适应新任务的训练模式。一般来说，元学习的目标是训练一个关于各种学习任务的模型，以便它可以推广到新的学习任务。主要有三种元学习方法：

1. 黑盒方法：通过标准的有监督学习来训练黑盒元学习者(例如神经网络)，以便输出任务的模型参数(PLM)。
2. 基于优化的方法：训练模型的初始参数，使得在用来自新任务的数据计算的一个或多个梯度步骤更新参数后，模型在该新任务上具有最大性能(和PLM不同，优化方法是指新任务中的模型可以快速调整参数)。
3. 基于度量的方法：又称非参数方法，学习通用匹配度量，该度量可以在所有分类任务中推广。

最近的一些工作考虑通过元学习来解决与KG相关的问题。例如，对于KG中的少样本链接预测，需要在只观察特定关系的少量样本的情况下预测三元组，GMatching和后续的基于度量的方法通过图结构和学习的嵌入来学习匹配度量；METAR和GANA利用基于优化的方法来快速调整关系嵌入。此外，GEN通过元学习框架解决了少样本KG外链接预测问题，该框架为连接到原始KG的少样本新实体的嵌入进行元学习。此外，在图表示学习方面，L2P-GNN通过元学习来预训练GNNs，以便GNNs处理下游任务的新KG，而MI-GNN在元学习范式下为每个图定制归纳式模型以实现跨图的归纳节点分类。

现有的KG元学习研究主要集中于将元学习应用于少样本场景。相反，在我们的工作中，我们的目标是使用元学习来模拟嵌入不可见实体的任务，这使得我们的模型得以在归纳设置下推广到具有不可见实体的KG中。

3.问题表述

知识图定义为$\mathcal{G}=(\mathcal{E},\mathcal{R},\mathcal{P})$，其中$\mathcal{E}$是实体集合，$\mathcal{R}$是关系集合。$\mathcal{P}=\{(h,r,t)\}\subseteq \mathcal{E}\times \mathcal{R}\times \mathcal{E}$是一组三元组。传统的KGE方法针对$\mathcal{E}$和$\mathcal{R}$的固定集合训练实体嵌入矩阵$\mathbf{E}\in {\mathbb{R}}^{|\mathcal{E}|\times d}$和关系嵌入矩阵$\mathbf{R}\in {\mathbb{R}}^{|\mathcal{R}|\times d}$，这样的嵌入应该遵循与特定KGE方法相关的得分函数$s$的假设，即嵌入应该满足合理性。更准确地说，$s(h,r,t)$应高于$s(h^{\prime },r^{\prime },t^{\prime })$ (其中$(h,r,t)\in \mathcal{P},(h^{\prime },r^{\prime },t^{\prime })\notin \mathcal{P}$)，并且$s(h,r,t)$是基于特定的KGE方法通过相应的嵌入来计算的。这种合理的嵌入可以用于各种KG内和KG外任务。

接下来，我们给出了归纳式KGE的定义。形式上，给定一组源KG–${\mathcal{G}}_S$和由源KG中未知实体组成的一组目标KG–${\mathcal{G}}_T$：
$$\begin{array}{rl}& {\mathcal{G}}_S={\left\{{\mathcal{G}}_s^{(i)}=\left({\mathcal{E}}_s^{(i)},{\mathcal{R}}_s^{(i)},{\mathcal{P}}_s^{(i)}\right)\right\}}_{i=1}^{n_s}\\ & {\mathcal{G}}_T={\left\{{\mathcal{G}}_t^{(i)}=\left({\mathcal{E}}_t^{(i)},{\mathcal{R}}_t^{(i)},{\mathcal{P}}_t^{(i)}\right)\right\}}_{i=1}^{n_t}\\ & \text{ s.t. }\left({\cup }_{i=1}^{n_t}{\mathcal{E}}_t^{(i)}\right)\cap \left({\cup }_{i=1}^{n_s}{\mathcal{E}}_s^{(i)}\right)=\varnothing ,\left({\cup }_{i=1}^{n_t}{\mathcal{R}}_t^{(i)}\right)\subseteq \left({\cup }_{i=1}^{n_s}{\mathcal{R}}_s^{(i)}\right)\end{array}\text{\hspace{1em}(1)}$$

归纳式KGE的目标是在源KG–${\mathcal{G}}_S$上学习一个函数$f$，其中$f$可以将${\mathcal{G}}_S$中的实体映射为具有上述合理性的嵌入，并且能够推广到目标KG–${\mathcal{G}}_T$。这种合理的嵌入可以用于目标KG上的各种KG内和KG外任务，并实现归纳式KGE。

值得注意的是，源KG和目标KG的数量不会影响$f$的训练和应用，至少对于本文的方法是这样。因此，为了简单起见，我们将考虑一个源KG和一个目标KG的场景来描述我们提出的框架，这意味着$n_s=n_t=1,{\mathcal{G}}_S=({\mathcal{E}}_s,{\mathcal{R}}_s,{\mathcal{P}}_s)$和${\mathcal{G}}_T=({\mathcal{E}}_t,{\mathcal{R}}_t,{\mathcal{P}}_t)$

4.模型方法

在概念上，我们专注于训练一个基于嵌入的模型来捕捉源KG中的元知识(即关于可转移结构模式的知识)，并将这些元知识传递给目标KG以产生合理的嵌入，从而使各种任务受益。这种元知识由前面提到的函数$f$隐式捕获，并可用于生成实体嵌入。为了实现元知识转移，我们的MorsE需要解决以下三个子问题：
$P1$ 如何对元知识进行建模？
$P2$ 如何在源KG–${\mathcal{G}}_S$中学习元知识？
$P3$ 如何使元知识适应目标KG–${\mathcal{G}}_T$？

4.1 元知识建模

在这一部分中，我们解决了子问题$P1$：如何对元知识建模。

重点设计了基于邻域结构信息生成实体嵌入的模块，模拟人类对一个新实体的认知过程。

对于一个实体来说，它最自然的结构信息可以通过它周围的关系来表示。因此，我们首先设计了一个实体初始化器，利用每个实体所关联的关系信息来初始化每个实体的嵌入。然而，这种初始化的实体嵌入是很初级的，因为它们只传递类型级别的信息，而不传递实例级别的信息。例如，如果两个实体都是关系Student_Of的头实体，我们只能推断他们是两个Student，但不能确切地推断他们是谁。

为了解决这个问题，我们引入了一个GNN调制器来根据每个实体的多跳邻域结构来调制每个实体的初始化嵌入。这两个模块都偏向于图对称。也就是说，具有相似连接关系和多跳邻域的实体将通过这两个模块获得相似的嵌入。因此，它们能够捕捉到KG中可转移的结构模式。

在下文中，我们描述了给定KG实例$\mathcal{G}=(\mathcal{E},\mathcal{R},\mathcal{P})$的实体初始化器和GNN调制器的过程。

4.1.1 实体初始化器

此模块用于捕获实体的类型级别的信息。因此，除了传统的关系嵌入矩阵$\mathbf{R}\in {\mathbb{R}}^{n_r\times d}$外，我们还设计了一个可学习的关系域嵌入矩阵${\mathbf{R}}^{\mathrm{dom}}\in {\mathbb{R}}^{n_r\times d}$和一个可学习的关系范围嵌入矩阵${\mathbf{R}}^{\mathrm{ran}}\in {\mathbb{R}}^{n_r\times d}$来表示每个关系的头部和尾部实体的隐含类型特征，其中$n_r$是关系的个数(当我们在${\mathcal{G}}_S$上训练该模型时，$n_r=|{\mathcal{R}}_s|$)，$d$是嵌入的维度。具体来说，在第4.2.2节中，$\mathbf{R}$保留了关系的内部语义，用于学习关系嵌入。包含隐式实体类型信息的${\mathbf{R}}^{dom}$和${\mathbf{R}}^{ran}$用于实体初始化。对于特定的关系$r$，其关系嵌入、关系域嵌入和关系范围嵌入分别表示为${\mathbf{R}}_r$、${\mathbf{R}}_r^{\mathrm{dom}}$和${\mathbf{R}}_r^{\mathrm{ran}}$，如图2(b)所示。

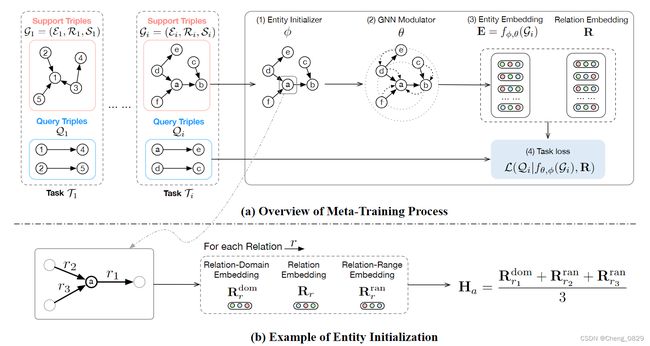
图2(b)：实体初始化举例

对于KG实例$\mathcal{G}=(\mathcal{E},\mathcal{R},\mathcal{P})$，MorsE基于它们的连接关系来初始化实体嵌入。具体地，对于实体$e\in \mathcal{E}$，其初始化嵌入${\mathbf{H}}_e$是通过其传入和传出关系的关系范围嵌入和关系域嵌入的平均值来计算的：
$${\mathrm{H}}_e=\frac{{\sum }_{r\in O(e)}{\mathbf{R}}_r^{\text{dom }}+{\sum }_{r\in \mathcal{I}(e)}{\mathbf{R}}_r^{\text{ran }}}{|O(e)|+|\mathcal{I}(e)|}\text{\hspace{1em}(2)}$$

其中$\mathcal{I}(e)=\{r|\exists x,(e,r,x)\in \mathcal{P}\}$表示实体$e$传入的关系集合，$\mathcal{O}(e)=\{r|\exists x,(e,r,x)\in \mathcal{P}\}$表示实体$e$传出的关系集合。图2(b)显示了使用${\mathbf{R}}^{dom}$和${\mathbf{R}}^{ran}$进行实体初始化的直观展示。

4.1.2 GNN调制器

该模块旨在通过来自多跳邻居的结构信息来捕获实体的实例级信息。到目前为止，一些前人的工作已经表明，GNN具有捕捉KG的局部结构信息的能力。因此，已初始化的实体嵌入的调整由GNN调制器存档。在R-GCN之后，我们的GNN调制器计算第$l$层中实体$e$的更新如下：
$${\mathbf{h}}_e^l=\alpha \left(\frac{1}{|\mathcal{N}(e)|}\sum _{(h,r)\in \mathcal{N}(e)}{\mathbf{W}}_r^l{\mathbf{h}}_h^{l-1}+{\mathbf{W}}_0^l{\mathbf{h}}_e^{l-1}\right)\text{\hspace{1em}(3)}$$

相当于所有包含实体$e$的三元组加权求平均,然后加上实体$e$本身的自循环(相当于偏差b)。

其中$\alpha$是激活函数ReLU；$\mathcal{N}(e)=\{(h,r)|(h,r,e)\in \mathcal{P}\}$表示实体$e$的直接传入邻居三元组的头实体和关系对的集合；${\mathbf{W}}_r^l$是在关系$r$第$l$层的特定关系变换矩阵；${\mathbf{W}}_0^l$是第$l$层中实体的自循环变换矩阵；${\mathbf{h}}_e^l$表示第$l$层中
实体$e$的隐藏实体表示，并且输入表示${\mathbf{h}}_e^0={\mathbf{H}}_e$。

为了充分利用每一层的隐藏实体表示，并让模型灵活地为每个实体利用最合适的邻域范围，我们应用了一种基于隐藏表示连接的跳跃知识(JK)结构，如下所示：
$${\mathrm{E}}_e={\mathbf{W}}^{\mathrm{JK}}\underset{l=0}{\overset{L}{⨁}}{\mathbf{h}}_e^l\text{\hspace{1em}(4)}$$
其中，${\mathrm{E}}_e$是实体$e$的最终实体嵌入；$⨁$表示连续连接；$L$是GNN调制器层的数量；${\mathbf{W}}^{\mathrm{JK}}$是将连接的隐藏表示转换为实体嵌入的矩阵。

4.1.3 总结

Step 1：给定一个KG–$\mathcal{G}=(\mathcal{E},\mathcal{R},\mathcal{P})$，实体初始化的过程为：
$$\mathbf{H}={\mathrm{INIT}}_{\theta }(\mathcal{G})\text{\hspace{1em}(5)}$$
其中$\mathbf{H}$是$\mathcal{E}$的初始化实体嵌入，$\theta$是包括${\mathbf{R}}^{dom}$和${\mathbf{R}}^{ran}$的参数集。

Step 2：接下来，GNN调制器的过程可以被看作是：
$$\mathbf{E}={\mathrm{MODULATE}}_{\varphi }(\mathcal{G},\mathbf{H})\text{\hspace{1em}(6)}$$
其中，$\mathbf{E}$是$\mathcal{E}$的输出实体嵌入，$\varphi$是GNN调制器的参数集。

整个过程可以看作是：
$$\mathbf{E}=f_{\theta ,\varphi }(\mathcal{G})={\mathrm{MODULATE}}_{\varphi }(\mathcal{G},{\mathrm{INIT}}_{\theta }(\mathcal{G}))\text{\hspace{1em}(7)}$$

如第三节所述，$f_{\theta ,\varphi }(\mathcal{G})$函数可以将KG中的实体映射到嵌入中。我们使用该函数及其参数来建模可传递的元知识，并在下一部分描述如何训练该函数以输出合理的实体嵌入。

4.2 元知识学习

在这一部分中，我们解决了子问题P2：如何通过元学习来学习源KG–${\mathcal{G}}_S$中的元知识，即学会如何学习。

在这一部分中，我们首先介绍了元学习的概念以及MorsE的相应设置。然后，我们描述了基于元学习的训练机制。

4.2.1 元学习设置

训练的目的是使上述$f_{\theta ,\varphi }$能够在给定任何具有未知实体的KG的情况下输出合理的实体嵌入，即学习产生实体嵌入。受“学会如何学习”这一元学习概念的启发，我们对MorsE进行了一系列任务的训练。具体地说，我们采样源KG–${\mathcal{G}}_S$中的一组子KG，并将这些子KG中的实体视为未知实体，用于模拟归纳设置中的目标KG。此外，为了给每个子KG制定一个任务，我们将三元组的一部分拆分为查询三元组，并将剩余的三元组视为支持三元组。支持三元组用于生成实体嵌入，查询三元组用于评估生成的嵌入的合理性和计算训练损失。在形式上，任务${\mathcal{T}}_i$定义如下：
$$\begin{array}{rl}& {\mathcal{T}}_i=\left({\mathcal{G}}_i=\left({\mathcal{E}}_i,{\mathcal{R}}_i,{\mathcal{S}}_i\right),Q_i\right)\\ & \text{ s.t. }{\mathcal{E}}_i\cap {\mathcal{E}}_s=\varnothing ,{\mathcal{R}}_i\subseteq {\mathcal{R}}_s\text{, }\end{array}\text{\hspace{1em}(8)}$$

其中${\mathcal{S}}_i$是支持三元组集合；${\mathcal{Q}}_i$是查询三元组集合；${\mathcal{E}}_s$和${\mathcal{R}}_s$分别是源KG–${\mathcal{G}}_s$的实体和关系集合。为了模拟(式1)中的目标KG归纳设置，我们将每个任务中的实体视为不可见，这可以通过重新标记实体来实现。由于这些任务模拟了具有不可见实体的目标KG的场景，因此我们针对这些任务的元训练模型可以自然地推广到目标KG。

4.2.2 元训练机制

在元学习设置之后，基于从${\mathcal{G}}_S$采样的任务来学习元知识，这也被称为元训练过程。在元训练过程中，对于每个任务${\mathcal{T}}_i=\left({\mathcal{G}}_i=\left({\mathcal{E}}_i,{\mathcal{R}}_i,{\mathcal{S}}_i\right),Q_i\right)$，基于其支持三元组获得实体嵌入，并通过其查询三元组来评估实体嵌入。从形式上讲，整个元训练目标是：
$$\underset{\theta ,\varphi ,\mathbf{R}}{\min }\sum _{i=1}^m{\mathcal{L}}_i=\underset{\theta ,\varphi ,\mathbf{R}}{\min }\sum _{i=1}^m\mathcal{L}\left(Q_i\mid f_{\theta ,\varphi }\left({\mathcal{G}}_i\right),\mathbf{R}\right)\text{\hspace{1em}(9)}$$

其中$\mathbf{R}\in {\mathbb{R}}^{|{\mathcal{R}}_s|\times d}$是所有关系的关系嵌入矩阵，$f_{\theta ,\varphi }({\mathcal{G}}_i)$用于输出当前任务中实体的嵌入矩阵(即${\mathcal{E}}_i$)；$\{\theta ,\varphi ,\mathbf{R}\}$为可学习参数；$m$表示采样任务的总数。元训练过程的直观举例如图2(a)所示。

图2(a)：元训练过程

训练损失的计算依赖于不同KGE方法的不同得分函数。例如，对于任务${\mathcal{T}}_i$，基于TransE的得分函数如下所示：
$$s(h,r,t)=-||{\mathbf{E}}_h+{\mathbf{R}}_r-{\mathbf{E}}_t||\text{\hspace{1em}(10)}$$
其中$\mathbf{E}=f_{\theta ,\varphi }({\mathcal{G}}_i)$；||·||表示L2范数。在我们的模型中可以使用许多传统的KGE方法。在本文中，我们使用了四种有代表性的方法，包括TransE、DistMult、ComplEx和RotatE，其得分函数的详细信息可以在表1中找到。

$$\begin{array}{lcc}\text{ 模型 }& \text{ 得分函数 }& \text{ 向量空间 }\\ \text{ TransE }& -\Vert \mathbf{h}+\mathbf{r}-\mathbf{t}\Vert & \mathbf{h},\mathbf{r},\mathbf{t}\in {\mathbb{R}}^d\\ \text{ DistMult }& {\mathbf{h}}^{\top }\mathrm{diag}(\mathbf{r})\mathbf{t}& \mathbf{h},\mathbf{r},\mathbf{t}\in {\mathbb{R}}^d\\ \text{ ComplEx }& \mathrm{Re}\left({\mathbf{h}}^{\top }\mathrm{diag}(\mathbf{r})\overline{\mathbf{t}}\right)& \mathbf{h},\mathbf{r},\mathbf{t}\in {\mathbb{C}}^d\\ \text{ RotatE }& -\Vert \mathbf{h}\circ \mathbf{r}-\mathbf{t}\Vert & \mathbf{h},\mathbf{r},\mathbf{t}\in {\mathbb{C}}^d\end{array}$$

表1：典型知识图模型的得分函数$s(h,r,t)；\mathbf{h},\mathbf{r},\mathbf{t}$是对应于$h,r,t$的嵌入；Re(·)表示复值向量的实向量分量；◦指的是Hadamard乘积。

在训练过程中，我们将基于自对抗性负采样的损失函数应用于每个任务的查询三元组$Q_i$，具体描述如下：
$$\begin{array}{rl}{\mathcal{L}}_i=& -\sum _{(h,r,t)\in Q_i}\log \sigma (\gamma +s(h,r,t))\\ & -\sum _{i=1}^{k}p\left(h_i^{\prime },r,t_i^{\prime }\right)\log \sigma \left(-\gamma -s\left(h_i^{\prime },r,t_i^{\prime }\right)\right)\end{array}\text{\hspace{1em}(11)}$$

损失函数分为两部分，前一部分是$Q_i$中的各个正三元组得分相加，后一部分是被破坏的k个三元组的得分“均值”(因为是负采样所以加上负号)

其中$\sigma$是Sigmoid函数；$\gamma$是固定边距；$k$是每个三元组的负样本数；$(h_i^{\prime },r,t_i^{\prime })$是通过被破坏的头实体或尾实体产生的第$i$个负三元组；$p(h_i^{\prime },r,t_i^{\prime })$是自对抗权重，计算如下:
$$p\left(h_j^{\prime },r,t_j^{\prime }\right)=\frac{\exp \beta s\left(h_j^{\prime },r,t_j^{\prime }\right)}{{\sum }_i\exp \beta s\left(h_i^{\prime },r,t_i^{\prime }\right)}\text{\hspace{1em}(12)}$$

$p(h_j^{\prime },r,t_j^{\prime })$之和为1，这保证了在(式11)中负采样求和时，最终的效果依然只相当于一个普通样本。

其中$\beta$是采样温度。

元知识的学习是通过本节描述的元学习在源KG–${\mathcal{G}}_S$上元训练第4.1节描述的模块。元训练后，函数$f_{\theta ,\varphi }$可在具有未知实体的任务中生成实体嵌入，并能推广到目标KG–${\mathcal{G}}_T$以实现归纳知识图嵌入。在${\mathcal{G}}_T$上生成实体嵌入并为下游任务提供服务的过程是元知识自适应，我们将在下文中对其进行描述。

4.3 元知识自适应

在这一部分中，我们解决了子问题$P3$：如何使元知识适应目标KG–${\mathcal{G}}_T$。

适应给定的目标KG–${\mathcal{G}}_T=({\mathcal{E}}_t,{\mathcal{R}}_t,{\mathcal{P}}_t)$是元知识迁移的反映，这一步骤很简单，因为从$f_{\theta ,\varphi }({\mathcal{G}}_T)$输出实体嵌入的能力允许MorsE灵活地适应各种KG内和KG外的任务。MorsE提出了两种元知识适应机制，如下所示。

4.3.1 冻结模式

在这种自适应模式下，我们冻结了元训练函数$f_{\theta ,\varphi }$的参数和关系嵌入矩阵$\mathbf{R}$。

然后，我们将MorsE看作一个实体嵌入产生器，并使用在目标KG上产生的实体嵌入来完成下游任务。例如，在链接预测中，这种嵌入可以用于直接进行链接预测并实现归纳链接预测。在问答中，这种嵌入可以被用作与QA对相关的KG的特征，并且SOTA QA模型可以在产生的嵌入之上被训练。

4.3.2 微调模式

在这种自适应模式下，元训练的MorsE的组件，包括$f_{\theta ,\varphi }$和$\mathbf{R}$，可以根据特定的任务进行训练。例如，在链接预测中，元训练的MorsE可以基于目标KG中的三元组进行微调。