机器学习与智能优化——利用简单遗传算法优化FCM
写在前面
本文的目的是要探讨利用简单遗传算法优化FCM,为什么要探讨这个话题呢?
因为单纯的FCM在处理大规模数据时,更加容易收敛到局部最优解,而将遗传算法加入后,可以降低FCM收敛到局部最优解的情况。
笔者之前写过两篇文章 《简单遗传算法优化简单一元函数(python)》 和 《好奇的小老鼠——使用FCM对图片像素进行聚类》 ,分别介绍了简单遗传算法SGA和FCM对图像像素的聚类,有兴趣的读者可以阅读参考。本文参考了《MATLAB智能算法30个案例分析(第2版)》中第20章《基于遗传模拟退火算法的聚类算法》的内容,只不过本文只利用了遗传算法对FCM进行了优化,并未加入模拟退火算法相关的内容。
遗传算法和FCM的原理这里就不再赘述,我们直奔主题。
聚类数据
本文的聚类数据由400个二维平面上的点组成,这些点构成4个集合,但彼此之间并没有明显的界限。本文通过使用单纯的FCM聚类和SGA优化初始聚类中心点后的FCM聚类来说明SGA的优势。
主体思路
利用简单遗传算法优化FCM主要思路是:在每次遗传算法迭代中,将种群中每个个体基因型解码作为FCM的初始聚类中心坐标(实数值坐标),然后根据解码后的初始聚类中心坐标运行FCM本身的优化方法,得到的FCM目标函数值可以作为遗传个体适应度的依据。得到最优初始聚类中心的同时,也就得到了与之对应的最终的最优聚类中心。
编码
大家知道,遗传算法中,编码是很重要的一个环节,本文对二维数据点进行聚类,编码是针对FCM的初始聚类中心进行的,将每个聚类中心的每一个维度的坐标值编码为二进制串,然后将其串联,形成最终的个体基因型。如下图,这里是示意图,每个坐标值的基因型长度需根据实际情况而定。
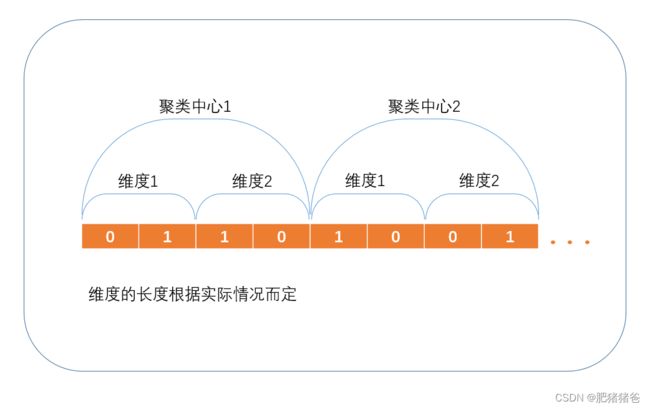
适应度函数
遗传个体的基因型通过解码都会都到一组初始聚类中心,把该初始聚类中心带入FCM,运行FCM本身的优化方法,得到该初始聚类中心对应的最佳聚类中心,同时也会得到对应的最佳目标函数值,鉴于FCM的目标函数值越小,聚类效果越好,可以对FCM目标函数值取反,作为遗传个体的适应度。
代码
FCM部分代码(fcm.py):
import numpy as np
class FCM:
def __init__(self, K, m=2, eps=0.05):
# 聚类个数
self.K = K
# 加权参数
self.m = m
# 终止容限
self.eps = eps
# 最优相似度矩阵
self.U = None
# 最终的聚类中心
self.centers = None
# 目标函数值
self.obj_val = None
def init_by_centers(self, data, centers):
# 初始化隶属度矩阵
self.U = np.random.random((len(data), self.K))
# 样本到聚类中心的距离
dist = np.zeros((len(data), self.K))
for i, x in enumerate(data):
for j, c in enumerate(centers):
dist[i][j] = np.linalg.norm(x - c, 2)
# 计算新的隶属度矩阵
for i, x in enumerate(data):
for j, c in enumerate(centers):
self.U[i][j] = 1./np.sum((dist[i][j]/dist[i]) ** (2/(self.m-1)))
# 最初的目标函数值
self.obj_val = np.sum((self.U ** self.m) * (dist ** 2))
def train(self, data):
if len(data.shape) == 1:
data = data[:, np.newaxis]
if self.U is None:
# 初始化隶属度矩阵
self.U = np.random.random((len(data), self.K))
# 保证每个样本属于所有类的概率是1
self.U = np.divide(self.U, np.sum(self.U, axis=1)[:, np.newaxis])
while True:
temp_U = self.U ** self.m
# 计算聚类中心
self.centers = np.divide(np.dot(temp_U.T, data), np.sum(temp_U.T, axis=1)[:, np.newaxis])
# 样本到聚类中心的距离
dist = np.zeros((len(data), self.K))
for i, x in enumerate(data):
for j, c in enumerate(self.centers):
dist[i][j] = np.linalg.norm(x - c, 2)
# 计算新的隶属度矩阵
for i, x in enumerate(data):
for j, c in enumerate(self.centers):
temp_U[i][j] = 1./np.sum((dist[i][j]/dist[i]) ** (2/(self.m-1)))
# 判断是否收敛
if np.sum(abs(temp_U-self.U)) < self.eps:
break
# 更新隶属度矩阵
self.U = temp_U
# 更新目标函数值
self.obj_val = np.sum((self.U ** self.m) * (dist ** 2))
# 返回样本最大隶属度对应的类别
return np.argmax(self.U, axis=1)
def __str__(self) -> str:
return f"K:{self.K}, m:{self.m}, eps:{self.eps}, U:{self.U}, centers:{self.centers}, dist: {self.dist}"
SGA优化FCM部分代码:
import math
from matplotlib import pyplot as plt
import random
import copy
from fcm import *
# 坐标变量的二进制位数
PRECI = 10
# 个体长度
CHROM_LEN = 20
# 种群大小
POP_SIZE = 10
# 最大遗传代数
MAX_GENERATION = 10
# 交叉概率
PC = 0.7
# 变异概率
PM = 0.01
# FCM指数
FCM_M = 2
# FCM容限
FCM_EPS = 10
# 解码用的参数
class FieldD:
def __init__(self, K, dim, dim_chrom_len, lb, ub):
# 聚类个数
self.K = K
# 维度个数
self.dim = dim
# 每个维度坐标的基因型长度
self.dim_chrom_len = dim_chrom_len
# 坐标下界
self.lb = lb
# 坐标上界
self.ub = ub
def __str__(self) -> str:
return f"K:{self.K}, dim:{self.dim}, dim_chrom_len{self.dim_chrom_len}, lb:{self.lb}, ub:{self.ub}"
# 解码
def bs2rv(chroms, fieldD: FieldD):
# 2的幂
two_pow = np.array([2 ** m for m in range(fieldD.dim_chrom_len)])[:, np.newaxis]
# 所有遗传个体的所有聚类中心坐标
centers_coordinates = []
# 遍历所有类别
for i in range(fieldD.K):
# 取出每个类别对应的基因型
center_start = i * fieldD.dim * fieldD.dim_chrom_len
center_chroms = chroms[:, center_start:center_start + fieldD.dim * fieldD.dim_chrom_len]
# 所有遗传个体的单个聚类中心坐标
coordinates = []
# 遍历所有维度
for j in range(fieldD.dim):
# 取出每个维度对应的基因型
dim_start = j * fieldD.dim_chrom_len
dim_chroms = center_chroms[:, dim_start:dim_start + fieldD.dim_chrom_len]
# 计算该维度基因型对应的表现型,即坐标值
temp = np.dot(dim_chroms[:, ::-1], two_pow)
dim_val = fieldD.lb + temp * (fieldD.ub - fieldD.lb) / (math.pow(2, fieldD.dim_chrom_len) - 1)
coordinates.append(dim_val)
centers_coordinates.append(np.concatenate(tuple(coordinates), axis=1)[:, np.newaxis, :])
return np.concatenate(tuple(centers_coordinates), axis=1)
# 选择(复制)操作
def select(population, pop_fitness):
# 新种群
new_pop = copy.copy(population)
# 当代个体适应度总和
fitness_sum = max(np.sum(pop_fitness), 0.0001)
# 当代个体累计适应度占比
cfitness = np.divide(pop_fitness, fitness_sum)
# 计算累计适应度占比
_triu = np.triu(np.array([1] * POP_SIZE * POP_SIZE).reshape((POP_SIZE, POP_SIZE)))
afitness = np.dot(cfitness[np.newaxis, :], _triu).flatten()
# 依据累计适应度占比进行选择复制,随机数大于对应的累计适应度占比,则进行复制
for k in range(POP_SIZE):
index = 0
while index < POP_SIZE and np.random.random() > afitness[index]:
index += 1
# 若无法找到要复制的其他个体,则沿用当前个体
if index < POP_SIZE:
new_pop[k] = population[index]
return new_pop
# 交叉操作
def crossover(population):
# 随机产生个体配对索引,类似于洗牌的效果
index = [i for i in range(POP_SIZE)]
for i in range(POP_SIZE):
point = random.randint(0, POP_SIZE - i - 1)
temp = index[i]
index[i] = index[point + i]
index[point + i] = temp
# 两个个体进行交叉
for i in range(0, POP_SIZE, 2):
if np.random.random() > PC:
# 随机选择交叉开始位置
cross_start = np.random.randint(0, CHROM_LEN - 2) + 1
# 需要交换的基因
cross_gene1 = population[index[i]][cross_start:]
cross_gene2 = population[index[i + 1]][cross_start:]
# 交叉操作
population[index[i]] = np.array(population[index[i]][0: cross_start].tolist() + cross_gene2.tolist())
population[index[i + 1]] = np.array(population[index[i + 1]][0: cross_start].tolist() + cross_gene1.tolist())
# 变异操作
def mutation(population):
for individual in population:
for i in range(CHROM_LEN):
# 随机数小于变异概率,则进行变异操作
if random.random() < PM:
individual[i] = 1 if individual[i] is 0 else 0
# 绘制进化过程
def draw_evolution(evolution):
x = [i for i in range(len(evolution))]
plt.plot(x, evolution)
# plt.show()
plt.savefig('fcm_sga_evolution.png', dpi=800)
plt.close()
# 得到种群所有个体的适应度值
def get_fitness(pop, data, f: FieldD):
# 解码为初始聚类中心
centers = bs2rv(pop, f)
# 所有个体的适应度
fitness = []
# 所有个体最终的聚类中心
final_centers = []
# 种群中样本类别
labels = []
# 循环所有初始聚类中心
for center in centers:
# FCM模型
fcm_model = FCM(K=f.K, m=FCM_M, eps=FCM_EPS)
# 通过初始聚类中心计算相似度矩阵
fcm_model.init_by_centers(data, center)
# 训练
_y = fcm_model.train(data)
# 记录信息
fitness.append(0-np.max([0., fcm_model.obj_val]))
final_centers.append(fcm_model.centers)
labels.append(_y)
return np.array(fitness), np.array(final_centers), np.array(labels)
# 绘制结果
def draw_result(data, best_centers, best_labels):
plt.scatter(data[:, 0], data[:, 1], c=best_labels, alpha=.1, edgecolors='black')
# 绘制最优解
plt.scatter(best_centers[:, 0], best_centers[:, 1], s=100, c='red', marker='*', zorder=2)
# plt.show()
plt.savefig('fcm_sga.png', dpi=800)
plt.close()
def run():
# 样本数量
N = 400
# 测试数据
X = np.random.rand(N, 2)
# 聚类个数
cluster_num = 4
# 维度个数
dim_num = 2
#
#
# 原始方法优化FCM
# FCM模型
my_fcm = FCM(K=cluster_num, m=FCM_M, eps=FCM_EPS)
# 训练
y = my_fcm.train(X)
print("单纯使用FCM聚类的结果:{}".format(my_fcm.obj_val))
# 绘图
plt.scatter(X[:, 0], X[:, 1], c=y, alpha=.1, edgecolors='black')
plt.scatter(my_fcm.centers[:, 0], my_fcm.centers[:, 1], s=100, c='red', marker='*')
# plt.show()
plt.savefig('fcm_only.png', dpi=800)
plt.close()
#
#
# 利用简单遗传算法进行优化
# 下界
lb = np.min(X)
# 上界
ub = np.max(X)
# 基因型解析参数
# K, dim, dim_chrom_len, lb, ub
f = FieldD(cluster_num, dim_num, PRECI, lb, ub)
global CHROM_LEN
CHROM_LEN = cluster_num * dim_num * PRECI
# 初始种群
population = np.random.randint(2, size=(POP_SIZE, CHROM_LEN))
# 初始种群适应度
pop_fitness, pop_centers, pop_labels = get_fitness(population, X, f)
# 初始种群最佳和最差个体索引
best_idx, worst_idx = np.argmax(pop_fitness), np.argmin(pop_fitness)
# 历史最佳个体及其适应度
current_best = population[best_idx]
current_best_fit = pop_fitness[best_idx]
# 最佳初始聚类中心
best_centers = pop_centers[best_idx]
# 最初分类结果
best_labels = pop_labels[best_idx]
# 进化过程,每一代的最佳个体的函数值
evolution = []
# 循环直到最大代数
for _ in range(MAX_GENERATION):
# 选择复制
population = select(population, pop_fitness)
# 交叉
crossover(population)
# 变异
mutation(population)
# 重新计算种群适应度
pop_fitness, pop_centers, pop_labels = get_fitness(population, X, f)
# 当前种群最佳和最差个体
best_idx, worst_idx = np.argmax(pop_fitness), np.argmin(pop_fitness)
# 利用精英模型执行进化操作,用历史最佳个体代替当代的最差个体
if pop_fitness[best_idx] > current_best_fit:
current_best = population[best_idx]
current_best_fit = pop_fitness[best_idx]
best_centers = pop_centers[best_idx]
best_labels = pop_labels[best_idx]
else:
population[worst_idx] = current_best
# 更新进化过程
evolution.append(0-round(current_best_fit, 4))
print("使用遗传算法优化FCM聚类的结果:{}".format(0-current_best_fit))
# 绘制进化过程
draw_evolution(evolution)
# 绘制结果
draw_result(X, best_centers, best_labels)
if __name__ == "__main__":
run()
FCM目标函数值对比:
单纯使用FCM聚类的结果:10.232015239531716
使用遗传算法优化FCM聚类的结果:10.169934869980217
结果显示,使用SGA优化FCM的效果更好。
单纯使用FCM进行聚类效果
使用SGA优化FCM的效果
遗传算法进化过程
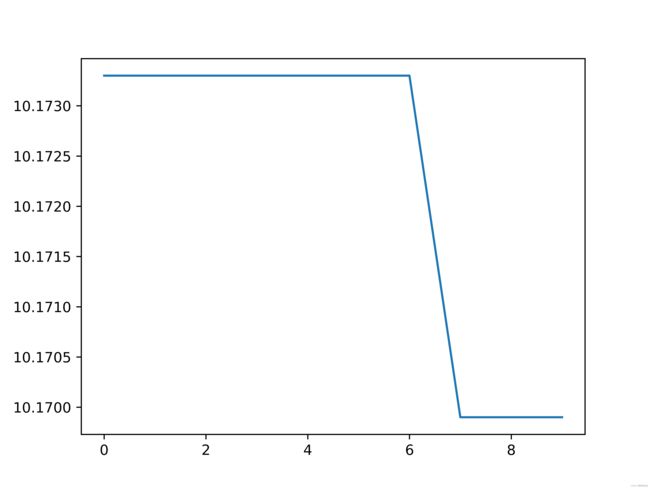
作者这水平有限,有不足之处欢迎留言指正