Python数据分析案例11——灰色预测法预测时间序列数据
本次案例来自2022华为杯第E题,第2小问。给定了2012.01-2022.03的土壤湿度的月度数据,需要预测2022.04-2023.12的土壤湿度的月度数据。典型的时间序列预测。
传统的时间序列预测肯定是ARIMA模型,可以参考我之前的文章。Python统计学10——时间序列分析自回归模型(ARIMA)
现在流行的方法肯定是深度学习的循环神经网络(RNN,LSTM,GRU),也可以参考我这篇文章。
Python深度学习05——Keras循环神经网络实现股价预测
本次我们要用的是一种比较数学的方法,灰色预测法。
灰色预测法是一种对含有不确定因素的系统进行预测的方法。在建立灰色预测模型之前,需先对原始时间序列进行数据处理,经过数据处理后的时间序列即称为生成列。灰色系统常用的数据处理方式有累加和累减两种。
灰色预测是以灰色模型为基础的,在众多的灰色模型中,GM(1,1)模型最为常用。
原理公式就不介绍了。
灰色预测法的通用性较强,一般的时间序列场合都适用,尤其适合那些规律性差且不清楚数据产生机理的情况。灰色预测模型的优点是预测精度高、模型可检验、参数估计方法简单、对小数据集有很好的预测效果;缺点是对原始数据序列的光滑度要求很高,在原始数据列光滑性较差的情况下灰色预测模型的预测精度不高,甚至通不过检验。
认识数据
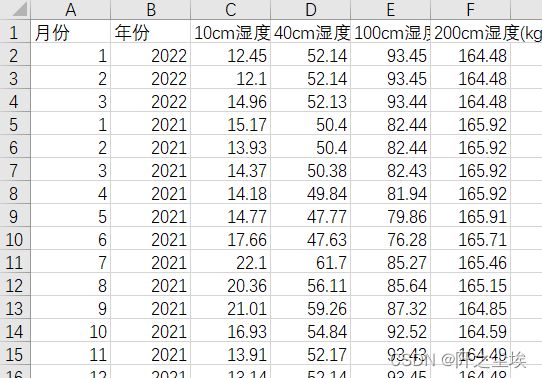
首先我们对问题要有清晰的认识。预测无非就是给一些数据,然后需要预测其他的一些数据,题目给的数据大概是这样的:
给定了2012.01-2022.03的土壤湿度的月度数据,需要预测2022.04-2023.12的土壤湿度的月度数据。
下面使用Python读取:
导入包:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
plt.rcParams ['font.sans-serif'] ='SimHei' #显示中文
plt.rcParams ['axes.unicode_minus']=False #显示负号读取数据,将前两列——年份和月份解析为时间,然后对时间索引进行排序,画折线图:
土壤湿度=pd.read_csv('土壤湿度.csv',parse_dates={'时间':[0,1]})
土壤湿度=土壤湿度.set_index('时间').sort_index()
土壤湿度.plot(figsize=(10,4))这就是初始数据,从2012.01-2022.03的土壤湿度的月度数据,需要预测2022.04-2023.12的土壤湿度数据。
灰色预测
定义灰色预测函数:
def GM11(x0): #自定义灰色预测函数
x1 = x0.cumsum() #1-AGO序列
z1 = (x1[:len(x1)-1] + x1[1:])/2.0 #紧邻均值(MEAN)生成序列
z1 = z1.reshape((len(z1),1))
B = np.append(-z1, np.ones_like(z1), axis = 1)
Yn = x0[1:].reshape((len(x0)-1, 1))
[[a],[b]] = np.dot(np.dot(np.linalg.inv(np.dot(B.T, B)), B.T), Yn) #计算参数
f = lambda k: (x0[0]-b/a)*np.exp(-a*(k-1))-(x0[0]-b/a)*np.exp(-a*(k-2)) #还原值
delta = np.abs(x0 - np.array([f(i) for i in range(1,len(x0)+1)]))
C = delta.std()/x0.std()
P = 1.0*(np.abs(delta - delta.mean()) < 0.6745*x0.std()).sum()/len(x0)
return f, a, b, x0[0], C, P #返回灰色预测函数、a、b、首项、方差比、小残差概率其实不理解原理也没什么,就按照我下面的流程用就行。
准备数据的值和时间索引:
new_reg_data = 土壤湿度.iloc[:,-4:] #取最后4列,即自己需要预测的四个变量
new_reg_data.index = pd.to_datetime(土壤湿度.index) #将原始数据的索引变为时间类型查看现在的数据:
new_reg_data可以看到时间,现在是123条。
由于需要预测2022.04-2023.12期间的四个变量,我们先要定义一个时间索引,一个月份一个月份的去预测。然后对每个变量进行循环,即每个变量都去拟合一个新的灰色预测函数。在每个月度预测完了后就给这一行赋值。这样能保证上一个预测值可以加入下一轮的预测里面。
index=pd.Series(pd.date_range('2022-04','2024-1',freq='M')).astype('datetime64[M]')
for i,ind in enumerate(index):
pred=[]
for c in new_reg_data.columns:
f = GM11(new_reg_data.loc[:,c].values)[0]
pred.append(f(1+len(new_reg_data)))
new_reg_data.loc[ind,:] = np.array(pred)查看结果:
new_reg_data可以看到时间,现在是144条。
画图看拟合效果:
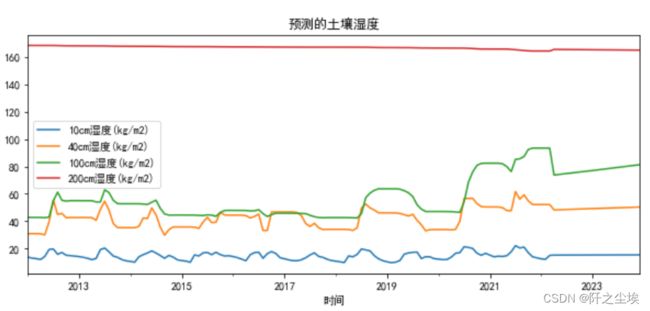
new_reg_data.plot(figsize=(10,4),title='预测的土壤湿度')
#plt.savefig('第二问的预测结果.jpg',dpi=128)emmmm,效果一般般,虽然预测出来的不是常数,但是预测的值也比较平滑。这也是灰色预测的一个特点。
当然建模比赛不会只用这么简单的模型....那肯定是神经网络什么的都往上整了,不过由于这个题目的数据量小,神经网络不太合适。灰色预测适合小数据集,该案例算是提供一个新的时间序列预测的思路吧