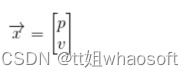嵌入式分享合集74
一、霍尔电流传感器的测量原理
霍尔电流传感器是依据霍尔效应原理,除了霍尔效应原理之外,还有磁通门技术和磁阻技术来测量电流,磁通门技术从原理上测量精度高于霍尔效应原理,通常用作测量仪器的开发,如高精度的实验室用电流传感器。这里主要介绍依据霍尔效应原理的电流传感器。
霍尔电流传感器分类
霍尔电流传感器在测量方式上可以分为两种,开环式霍尔电流传感器和闭环式霍尔电流传感器。这两种类型的传感器在结构上来说闭环式传感器比开环式多了一个线圈,在精度上闭环式要优于开环式。
开环式霍尔电流传感器测量原理
开环式霍尔电流传感器由铁芯、霍尔芯片、运放等关键元器件构成。当电流穿过铁芯时会在铁芯上感应出磁场,铁芯将磁场聚集于豁口处被霍尔元器件感应到,从而感应出相应的电压,该电压被运放处理后输出,运放所输出的电压信号和原边电流满足一定的线性关系,从而将被测电流信号转化为电压信号,单片机采样该电压信号就可计算出被测电流的大小,从而实现测量电流的作用。开环式霍尔电流传感器又叫直测式。由于体积受限,许多芯片级的霍尔电流芯片都是用开环测量原理,如ACS712、ACS758等。
闭环霍尔电流传感器工作原理
与开环霍尔电流传感器相比,闭环霍尔电流传感器多了一个补偿线圈,该线圈缠绕在铁芯上。当电流传感器通过铁芯时,铁芯感应出磁场,霍尔元器件将磁场转化成电压,该电压被运放处理后驱动电路产生一个补偿电流,该补偿电流流过线圈产生一个磁场,该磁场与原边电流产生的磁场大小相等方向相反,从而抵消原边磁场,处于磁平衡状态。所以该补偿电流就是原边电流缩放后的,缩放比例与补偿线圈的圈数呈线性关系。闭环式霍尔电流传感器又叫间接测量法。
霍尔电流关键元器件-霍尔元器件
在霍尔电流传感器中,霍尔元器件是关键元器件,其性能影响着产品的性能。霍尔元器件的作用是将一定范围内的磁通量转化成电压信号。如下图所示,霍尔元器件将50mT内的磁通密度转化成电压信号。所以选用该芯片时,一定不要让铁芯产生的磁通密度超过50mT。
霍尔电流关键元器件-铁芯
霍尔电流传感器是由结构和电路紧密配合的一个产品,这其中,霍尔元器件的高度、位置,铁芯的材料、长度、横截面积都决定着产品的性能。在设计产品时,一定要注意严格根据测量范围计算铁芯的磁路长度、铁芯的横截面积、磁隙间距以及霍尔芯片的高度。当然这部分的计算是设计霍尔电流传感器中最核心的部分。
二、霍尔效应的工作原理
霍尔效应是由带电粒子(如电子)相应电场和磁场的相互作用引起的。更为形象生动的大家可以看下面这个霍尔效应原理动画图。
当导电板连接到带有电池的电路时,电流开始流动。电荷载体将沿着从板的一端到另一端的线性路径。电荷载流子的运动导致磁场的产生。当磁体靠近板放置时,电荷载流子的磁场会发生畸变。这扰乱了电荷载流子的直线流动。扰乱电荷载流子流动方向的力称为洛伦兹力。
由于电荷载流子磁场的畸变,带负电的电子将偏转到板的一侧,而带正电的空穴将偏转到板的另一侧。在板的两侧之间会产生一个电位差,称为霍尔电压,可以用仪表测量。
霍尔效应和洛伦兹力,蓝色箭头 B 表示垂直穿过导电板的磁场
霍尔效应原理表明:当将载流导体或半导体引入垂直磁场时,可以在电流路径成直角的位置测量电压。
霍尔电压表示为 VH 由公式给出:
-
VH 是导电板上的霍尔电压
-
I 是流过传感器的电流
-
B 是磁场强度
-
q 是电荷
-
n 是每单位体积的电荷载流子的数量
-
d 是传感器的厚度
当传感器周围的磁通密度超过某个预设阈值时,传感器会检测到它并产生称为霍尔电压 VH 的输出电压。具体的原理如下图所示。
霍尔效应传感器基本上由一块薄薄的矩形 p 型半导体材料组成,例如砷化镓 (GaAs)、锑化铟 (InSb) 或砷化铟 (InAs),其自身通过连续电流。
当霍尔效应传感器放置在磁场中时,磁通量线对半导体材料施加一个力,使载流子、电子和空穴偏转到半导体板的任一侧。电荷载流子的这种运动是它们穿过半导体材料时所经历的磁力的结果。
当这些电子和空穴向侧面移动时,由于这些电荷载流子的积累,在半导体材料的两侧之间会产生电位差。然后,电子通过半导体材料的运动受到与其成直角的外部磁场的影响,这种影响在扁平矩形材料中更大。
霍尔效应提供有关磁极类型和磁场大小的信息。例如,南极会使设备产生电压输出,而北极则不会产生任何影响。通常,霍尔效应传感器和开关设计为在不存在磁场时处于“关闭”状态(开路状态)。它们只有在受到足够强度和极性的磁场时才会“打开”(闭路条件)。
在最简单的形式中,传感器作为模拟传感器工作,直接返回电压。在已知磁场的情况下,可以确定其与霍尔板的距离。使用传感器组,可以推断出磁体的相对位置。
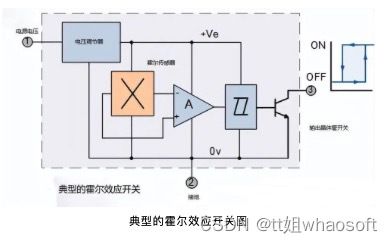
通常,霍尔效应传感器与允许设备以数字(开/关)模式运行的电路相结合,并且在此配置中可能被称为开关。下图为包含两个磁铁的轮子经过霍尔效应传感器,可以明显的看到灯的变化。
大多数霍尔效应器件不能直接切换大型电气负载,因为它们的输出驱动能力非常小,大约为 10 到 20mA。对于大电流负载,在输出中添加一个集电极开路(电流吸收)NPN 晶体管。如下图所示: whaosoft aiot http://143ai.com
该晶体管在其饱和区域中作为 NPN 灌电流开关工作,只要施加的磁通密度高于“ON”预设点的磁通密度,就会将输出端子短接到地。
输出开关晶体管可以是发射极开路晶体管、集电极开路晶体管配置或两者都提供推挽输出类型配置,该配置可以吸收足够的电流以直接驱动许多负载,包括继电器、电机、LED 和灯。
霍尔效应传感器可提供线性或数字输出。线性(模拟)传感器的输出信号直接取自运算放大器的输出,输出电压与通过霍尔传感器的磁场成正比。该输出霍尔电压为:
-
V H是以伏特为单位的霍尔电压
-
R H是霍尔效应系数
-
I是流过传感器的电流,单位为安培
-
t是传感器的厚度,单位为 mm
-
B是特斯拉的磁通量密度
线性或模拟传感器提供连续的电压输出,该输出随强磁场增加而随着弱磁场减少。在线性输出霍尔效应传感器中,随着磁场强度的增加,来自放大器的输出信号也会增加,直到它开始因施加电源的限制而饱和。
磁场的任何额外增加都不会对输出产生影响,但会使其更加饱和。
霍尔传感器测量方法--磁场的运动路径
霍尔效应传感器由磁场激活,在许多应用中,该设备可以通过连接到移动轴或设备的单个永磁体来操作。有许多不同类型的磁铁运动,例如“正面”、“侧身”、“推拉”或“推-推”等感应运动。
使用每种类型的配置,以确保最大灵敏度,磁通线必须始终垂直于设备的感应区域,并且必须具有正确的极性。
此外,为了确保线性,需要高场强磁铁,以便为所需的运动产生较大的场强变化。检测磁场有多种可能的运动路径,以下是使用单个磁体的两种更常见的传感配置:正面检测和侧向检测。
1、霍尔传感器测量方法--正面检测
顾名思义,“正面检测”要求磁场垂直于霍尔效应传感设备,并且为了检测,它直接朝向有源面接近传感器。一种“正面”的方法。
这种正面方法会产生一个输出信号VH,它在线性器件中表示磁场强度,即磁通量密度,它是距霍尔效应传感器的距离的函数。距离越近,磁场越强,输出电压越大,反之亦然。
线性器件还可以区分正磁场和负磁场。非线性装置可以在远离磁铁的预设气隙距离处触发输出“ON”,以指示位置检测。
2、霍尔传感器测量方法--侧身检测
第二种传感配置是“横向检测”。这需要在霍尔效应元件的表面上横向移动磁铁。
当磁场在固定气隙距离内穿过霍尔元件的表面时,侧向或滑过检测对于检测磁场的存在很有用,例如,计算旋转磁铁或电机的旋转速度。
根据磁场通过传感器零场中心线时的位置,可以产生表示正输出和负输出的线性输出电压。这允许定向运动检测,它可以是垂直的也可以是水平的。
霍尔传感器--位置检测器
根据设备的类型(无论是数字的还是线性的),有许多不同的方法可以将霍尔效应传感器连接到电气和电子电路。一个非常简单且易于构建的实例如下图:
当不存在磁场(0 )时,正面位置检测器将“关闭”。当永磁体南极(正高斯)垂直移动到霍尔效应传感器的有效区域时,设备将“打开”并点亮 LED。一旦切换“ON”,霍尔效应传感器将保持“ON”。
霍尔传感器优缺点
优点
霍尔效应传感器可以用作电子开关。
-
这种开关的成本低于机械开关,而且更可靠。
-
它的工作频率最高可达 100 kHz。
-
它不会受到触点反弹的影响,因为使用了具有滞后功能的固态开关而不是机械触点。
-
由于传感器采用密封包装,因此不会受到环境污染物的影响。因此,它可以在恶劣的条件下使用。
对于线性传感器(用于磁场强度测量),霍尔效应传感器:
-
可以测量范围广泛的磁场
-
可以测量北极或南极磁场
-
可以是平的
缺点
霍尔效应传感器提供的测量精度远低于磁通门磁力计或基于磁阻的传感器。此外,霍尔效应传感器漂移显着,需要补偿。
三、卡尔曼滤波算法原理
因为uwb啊 视觉啊等一切都用这了 就也发这了~~ 以后在挪把
一、什么是卡尔曼滤波?
你可以在任何含有不确定信息的动态系统中使用卡尔曼滤波,对系统下一步的走向做出有根据的预测,即使伴随着各种干扰,卡尔曼滤波总是能指出真实发生的情况。
在连续变化的系统中使用卡尔曼滤波是非常理想的,它具有占用内存小的优点(除了前一个状态量外,不需要保留其它历史数据),并且速度很快,很适合应用于实时问题和嵌入式系统。
在Google上找到的大多数关于实现卡尔曼滤波的数学公式看起来有点晦涩难懂,这个状况有点糟糕。实际上,如果以正确的方式看待它,卡尔曼滤波是非常简单和容易理解的,下面我将用漂亮的图片和色彩清晰的阐述它,你只需要懂一些基本的概率和矩阵的知识就可以了。
二、我们能用卡尔曼滤波做什么?
用玩具举例:你开发了一个可以在树林里到处跑的小机器人,这个机器人需要知道它所在的确切位置才能导航。
注意这个状态只是关于这个系统基本属性的一堆数字,它可以是任何其它的东西。在这个例子中是位置和速度,它也可以是一个容器中液体的总量,汽车发动机的温度,用户手指在触摸板上的位置坐标,或者任何你需要跟踪的信号。
这个机器人带有GPS,精度大约为10米,还算不错,但是,它需要将自己的位置精确到10米以内。树林里有很多沟壑和悬崖,如果机器人走错了一步,就有可能掉下悬崖,所以只有GPS是不够的。
或许我们知道一些机器人如何运动的信息:例如,机器人知道发送给电机的指令,知道自己是否在朝一个方向移动并且没有人干预,在下一个状态,机器人很可能朝着相同的方向移动。当然,机器人对自己的运动是一无所知的:它可能受到风吹的影响,轮子方向偏了一点,或者遇到不平的地面而翻倒。所以,轮子转过的长度并不能精确表示机器人实际行走的距离,预测也不是很完美。
GPS 传感器告诉了我们一些状态信息,我们的预测告诉了我们机器人会怎样运动,但都只是间接的,并且伴随着一些不确定和不准确性。但是,如果使用所有对我们可用的信息,我们能得到一个比任何依据自身估计更好的结果吗?回答当然是YES,这就是卡尔曼滤波的用处。
三、卡尔曼滤波是如何看到你问题的
下面我们继续以只有位置和速度这两个状态的简单例子做解释。
我们并不知道实际的位置和速度,它们之间有很多种可能正确的组合,但其中一些的可能性要大于其它部分:
在上图中,位置和速度是不相关的,这意味着由其中一个变量的状态无法推测出另一个变量可能的值。下面的例子更有趣:位置和速度是相关的,观测特定位置的可能性取决于当前的速度:
这种情况是有可能发生的,例如,我们基于旧的位置来估计新位置。如果速度过高,我们可能已经移动很远了。如果缓慢移动,则距离不会很远。跟踪这种关系是非常重要的,因为它带给我们更多的信息:其中一个测量值告诉了我们其它变量可能的值,这就是卡尔曼滤波的目的,尽可能地在包含不确定性的测量数据中提取更多信息!
四、使用矩阵来描述问题
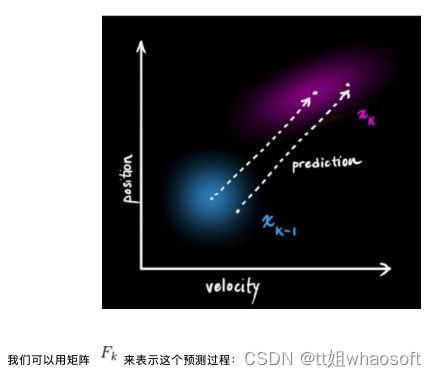
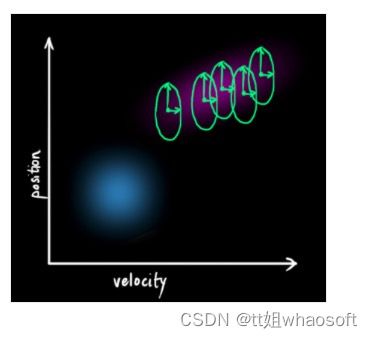
(当然,在这里我们只用到了位置和速度,实际上这个状态可以包含多个变量,代表任何你想表示的信息)。接下来,我们需要根据当前状态(k-1 时刻)来预测下一状态(k 时刻)。记住,我们并不知道对下一状态的所有预测中哪个是“真实”的,但我们的预测函数并不在乎。它对所有的可能性进行预测,并给出新的高斯分布。
它将我们原始估计中的每个点都移动到了一个新的预测位置,如果原始估计是正确的话,这个新的预测位置就是系统下一步会移动到的位置。那我们又如何用矩阵来预测下一个时刻的位置和速度呢?下面用一个基本的运动学公式来表示:
五、外部控制量
我们并没有捕捉到一切信息,可能存在外部因素会对系统进行控制,带来一些与系统自身状态没有相关性的改变。
外部干扰
如果这些状态量是基于系统自身的属性或者已知的外部控制作用来变化的,则不会出现什么问题。
但是,如果存在未知的干扰呢?例如,假设我们跟踪一个四旋翼飞行器,它可能会受到风的干扰,如果我们跟踪一个轮式机器人,轮子可能会打滑,或者路面上的小坡会让它减速。这样的话我们就不能继续对这些状态进行跟踪,如果没有把这些外部干扰考虑在内,我们的预测就会出现偏差。
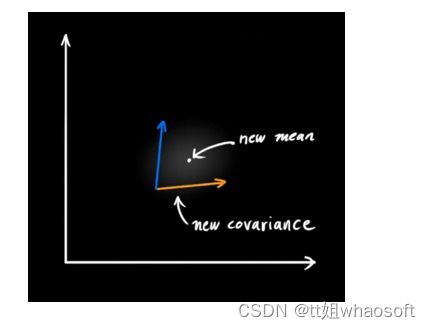
在每次预测之后,我们可以添加一些新的不确定性来建立这种与“外界”(即我们没有跟踪的干扰)之间的不确定性模型:
这产生了具有不同协方差(但是具有相同的均值)的新的高斯分布。
由上式可知,新的最优估计是根据上一最优估计预测得到的,并加上已知外部控制量的修正。
而新的不确定性由上一不确定性预测得到,并加上外部环境的干扰。
六、用测量值来修正估计值
我们可能会有多个传感器来测量系统当前的状态,哪个传感器具体测量的是哪个状态变量并不重要,也许一个是测量位置,一个是测量速度,每个传感器间接地告诉了我们一些状态信息。
我们可以计算出传感器读数的分布,用之前的表示方法如下式所示:
卡尔曼滤波的一大优点就是能处理传感器噪声,换句话说,我们的传感器或多或少都有点不可靠,并且原始估计中的每个状态可以和一定范围内的传感器读数对应起来。
从测量到的传感器数据中,我们大致能猜到系统当前处于什么状态。但是由于存在不确定性,某些状态可能比我们得到的读数更接近真实状态。
现在我们有了两个高斯分布,一个是在预测值附近,一个是在传感器读数附近。
剩下的就是重叠部分了,这个重叠部分的均值就是两个估计最可能的值,也就是给定的所有信息中的最优估计。
瞧!这个重叠的区域看起来像另一个高斯分布。
如你所见,把两个具有不同均值和方差的高斯分布相乘,你会得到一个新的具有独立均值和方差的高斯分布!下面用公式讲解。
七、融合高斯分布
八、将所有公式整合起来
九、总结
以上所有公式中,你只需要用到式(7)、(18)、(19)。(如果忘了的话,你可以根据式(4)和(15)重新推导一下)
我们可以用这些公式对任何线性系统建立精确的模型,对于非线性系统来说,我们使用扩展卡尔曼滤波,区别在于EKF多了一个把预测和测量部分进行线性化的过程。