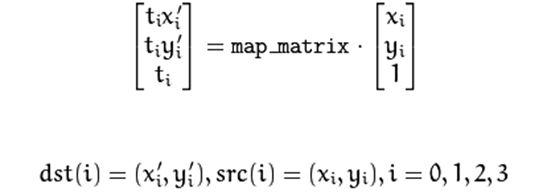OpenCV 透视变换 & 图像拼接
A:OpenCV 透视变换
一:OpenCV透视变换的概念
仿射变换(affine transform)与透视变换(perspective transform)在图像还原、图像局部变化处理方面有重要意义。通常,在2D平面中,仿射变换的应用较多,而在3D平面中,透视变换又有了自己的一席之地。两种变换原理相似,结果也类似,可针对不同的场合使用适当的变换。
仿射变换和透视变换的数学原理不需深究,在应用层面,仿射变换是图像基于3个固定顶点的变换,如下图所示:
二:透视变换工作原理
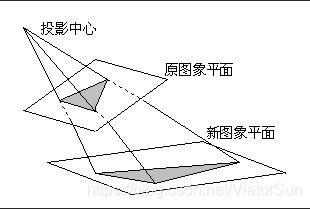
透视变换(Perspective Transformation)的本质是将图像投影到一个新的视平面,其通用变换公式为:
(u,v)为原始图像像素坐标,(x=x’/w’,y=y’/w’)为变换之后的图像像素坐标。透视变换矩阵图解如下:
透视变换工作原理
仿射变换(Affine Transformation)可以理解为透视变换的特殊形式。透视变换的数学表达式为:
所以,给定透视变换对应的四对像素点坐标,即可求得透视变换矩阵;反之,给定透视变换矩阵,即可对图像或像素点坐标完成透视变换,如下图所示:
三:findHomography函数
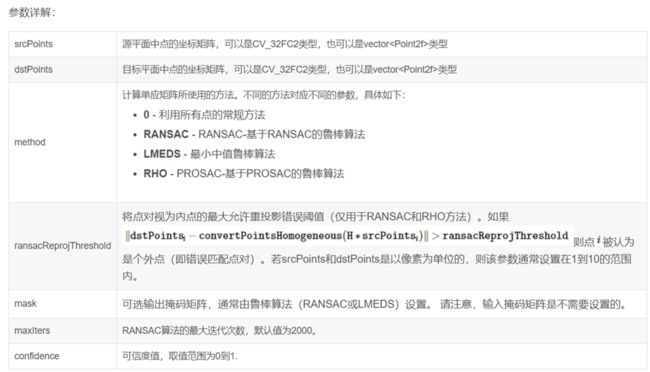
这里重点分析findHomography函数参数和使用方法
findHomography: 计算多个二维点对之间的最优单映射变换矩阵 H(3行x3列) ,使用最小均方误差或者RANSAC方法。函数功能:找到两个平面之间的变换矩阵。
Mat cv::findHomography ( InputArray srcPoints,
InputArray dstPoints,
int method = 0,
double ransacReprojThreshold = 3,
OutputArray mask = noArray(),
const int maxIters = 2000,
const double confidence = 0.995
)
四:warpPerspective函数
void warpPerspective(InputArray src, OutputArray dst, InputArray M, Size dsize, int flags=INTER_LINEAR, int borderMode=BORDER_CONSTANT, const Scalar& borderValue=Scalar())warpPerspective参数说明:
1.src – 输入图像2.dst – 大小为dsize且类型与src相同的输出图像3.M – 3×3变换矩阵4.dsize – 输出图像的大小图中红点即为固定顶点,在变换先后固定顶点的像素值不变,图像整体则根据变换规则进行变换
同理,透视变换是图像基于4个固定顶点的变换,如图所示:
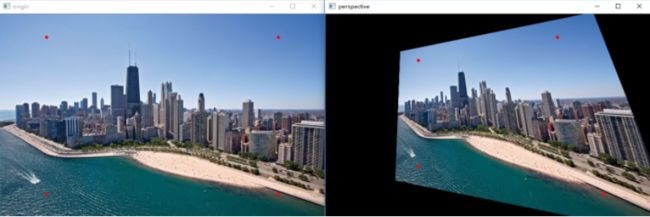
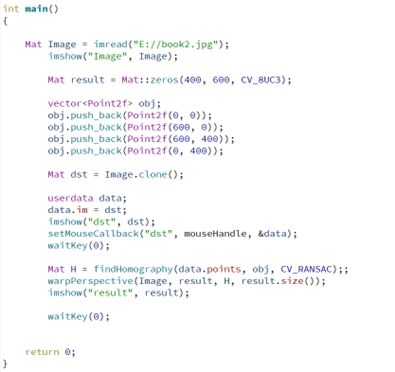
五:透视变换案例
这个例子中通过鼠标点击图片进行区域读取
六:getPerspectiveTransform函数
C++方式一:Mat getPerspectiveTransform(InputArray src, InputArray dst)
C++方式二:Mat getPerspectiveTransform(const Point2f src[], const Point2f dst[])
getPerspectiveTransform参数说明:
src – 源图像中四边形顶点的坐标
dst – 目标图像中相应四边形顶点的坐标。
该函数计算透视变换的3乘3矩阵,以便实现以下计算:
代码示例:
int main( )
{
Point2f srcTri[4];
Point2f dstTri[4];
Mat warpPerspective_mat( 3, 3, CV_32FC1 );
Mat src, warpPerspective_dst;
/// Load the image
src = imread( "lena.bmp", IMREAD_COLOR );
/// Set the dst image the same type and size as src
warpPerspective_dst = Mat::zeros( src.rows, src.cols, src.type() );
/// 设置三组点,求出变换矩阵
srcTri[0] = Point2f( 0,0 );
srcTri[1] = Point2f( src.cols - 1,0 );
srcTri[2] = Point2f( 0,src.rows - 1);
srcTri[3] = Point2f(src.cols - 1,src.rows - 1);
dstTri[0] = Point2f( 0,src.rows*0.13 );
dstTri[1] = Point2f( src.cols*0.9,0 );
dstTri[2] = Point2f( src.cols*0.2,src.rows*0.7 );
dstTri[3] = Point2f( src.cols*0.8,src.rows );
//计算3个二维点对之间的仿射变换矩阵(2行x3列)
warpPerspective_mat = getPerspectiveTransform( srcTri, dstTri );
//应用仿射变换,可以恢复出原图
warpPerspective( src, warpPerspective_dst, warpPerspective_mat, src.size() );
//显示结果
namedWindow( source_window, WINDOW_AUTOSIZE );
imshow( source_window, src );
namedWindow( warpPerspective_window, WINDOW_AUTOSIZE );
imshow( warpPerspective_window, warpPerspective_dst );
/// 等待,直到用户退出
waitKey(0);
return 0;
}
B:OpenCV 图像拼接
一:OpenCV图像特征采集
特征提取:
一幅图中总存在着一些独特的像素点,这些点我们可以认为就是这幅图的特征,成为特征点。
计算机视觉领域特征提取:
获取一幅图中存在着一些独特的像素点。
解决两个问题:
1、提取图片中的特征点
2、解决尺度不变性问题,不同大小的图片获取到的特征是一样的。
3、提取到的特征点要稳定,能被精确定位。
二:特征提取算法
三:特征提取
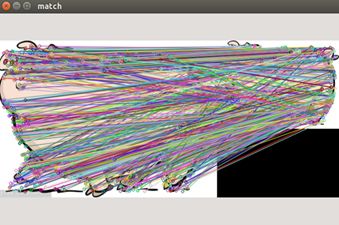
提取到的特征很粗糙,不是很精确的特征点,导致效果很差。
去粗取精,获取优秀的匹配点。
四:特征取精
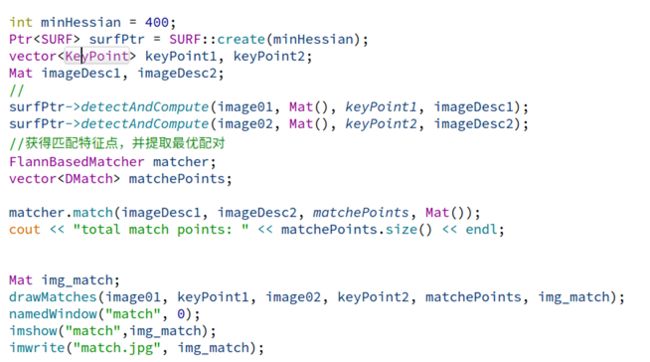
取一幅图像中的一个SIFT关键点,并找出其与另一幅图像中欧式距离最近的前两个关键点,在这两个关键点中,如果最近的距离除以次近的距离得到的比率ratio少于某个阈值T,则接受这一对匹配点。
五:OpenCV透视转换
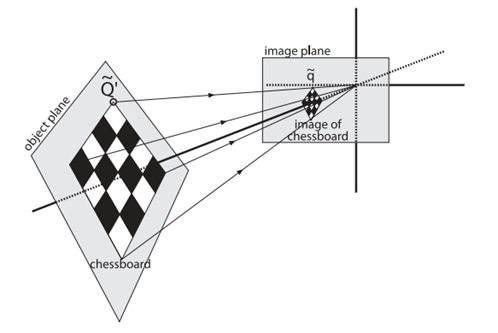
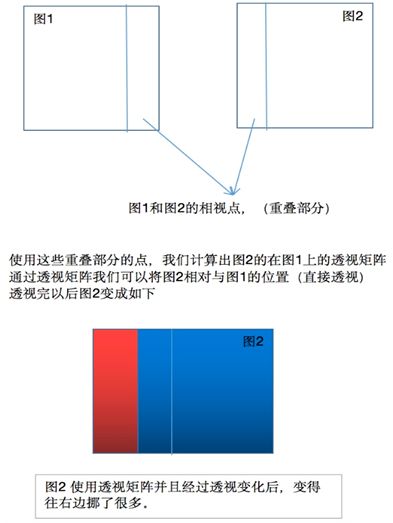
透视变换是按照物体成像投影规律进行变换,即将物体重新投影到新的成像平面。透视变换常用于机器人视觉导航研究中,由于相机视场与地面存在倾斜角使得物体成像产生畸变,通常通过透视变换实现对物体图像的校正。
六:透视矩阵
[u,v,w] 表示当前平面坐标的x,y,z,如果是平面,那么z=1。
[x',y',z'] 表示目标平面坐标的x,y,z,如果是平面,那么z=1。
通过以上公式,我们可以将透视矩阵理解为:透视矩阵是原始平面可目标平面之间的一种转换关系。
七:获取特征矩阵
根据图像的4个顶点来获取特征矩阵
cv::Mat cv::getPerspectiveTransform( // 返回3x3透视变换矩阵
const cv::Point2f* src, // 源图像四个顶点坐标(点数组)
const cv::Point2f* dst // 目标图像上四个顶点的坐标(点数组)
);函数来计算透视矩阵H(3*3)
findHomography (
InputArray srcPoints,//源平面中点的坐标矩阵.vector类型
InputArray dstPoints,//目标平面中点的坐标矩阵,vector类型
int method = 0,
double ransacReprojThreshold = 3,
OutputArray mask = noArray(),
const int maxIters = 2000,
const double confidence = 0.995
) 使用cv::warpPerspective()进行透视变换
void cv::warpPerspective(
cv::InputArray src, // 输入图像
cv::OutputArray dst, // 输出图像
cv::InputArray M, // 3x3 变换矩阵
cv::Size dsize, // 目标图像大小
int flags = cv::INTER_LINEAR, // 插值方法
int borderMode = cv::BORDER_CONSTANT, // 外推方法
const cv::Scalar& borderValue = cv::Scalar() //常量边界时使用
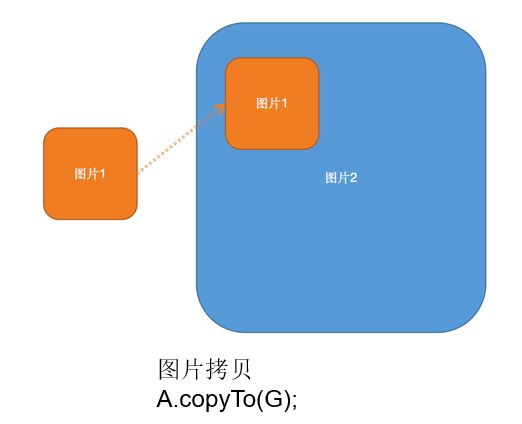
);八:图像拷贝
图像拷贝:将一副图像拷贝到另一副图像上的过程: