数据结构算法-栈技术点

基本描述

生活当中只有一个出口的瓶子,装羽毛球的筒子,玩具枪有子弹的弹夹, 水枪 管道,北京胡同 水龙头 等等

游戏:老鹰捉小鸡
无论你怎么抓小只因都是抓取最后一个

出口 只有一个,入口也只有一个 尾部

栈原理精讲

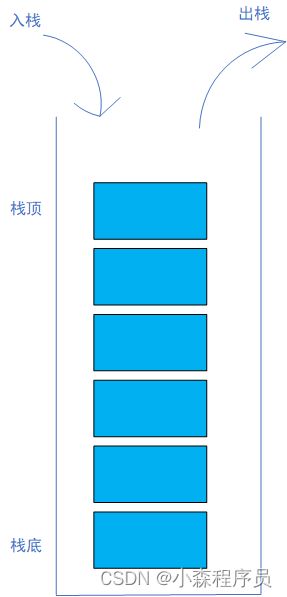
栈是一个后进先出 的一种数据结构,
栈:受限线性结构;
栈::只允许后面出栈 后面入栈
栈的底部叫栈底
栈的顶部叫栈顶

出栈的时候有两种方法:
物理删除,逻辑删除
所谓的物理删除 该怎么删除就这么删除
逻辑删除:不去直接删除 而是直接访问下一个元素 所谓的:忽略 不去直接删除 好处 避免了大量的移动 效率高

**栈不能被遍历 **

栈的算法实现:

顺序栈

顺序栈:用顺序表来做的栈 效果如上

初始化栈
尾部添加元素(往后添加)
尾部删除元素(逻辑删除)
访问栈顶
获取栈的元素个数

顺序栈

//元素类型
using ElementType = user-defined;

//顺序栈辅助
struct _SeqStackAuxiliary {

	ElementType* back;
};

//顺序栈辅助
using  SeqStackAuxiliary = struct _SeqStackAuxiliary;

//顺序栈
struct _SeqStack {

	ElementType* element;
	size_t Size;
	SeqStackAuxiliary Auxiliary;
};

using  SeqStack = struct _SeqStack;

//最大的顺序栈元素大小
const size_t SeqStackMaxSize = 1000;

顺序栈 操作算法声明

//初始化顺序栈
void initStack(SeqStack& Stack);

//入栈
void push_Stack(SeqStack& Stack, const ElementType& e);

//访问栈顶元素
ElementType& TopStack(SeqStack& Stack);

//顺序栈已满
bool fullStack(const SeqStack& Stack);

//顺序栈已空
bool emptyStack(const SeqStack& Stack);

//出栈
void pop_Stack(SeqStack& Stack);

//栈元素大小
const size_t& StackSize(const SeqStack& Stack);

//销毁顺序栈
void destroyStack(SeqStack& Stack);

//顺序栈辅助
SeqStackAuxiliary这个好像没有见过 全网的文章都没有 那是要不然怎么做原创嘛,
从定义来看

 ElementType* back;//方便添加元素 方便访问 back-1的元素  也就是栈顶元素

#include "SeqStack.h"
#include

const size_t zero = 0u;

void initStack(SeqStack& Stack){
	
	Stack.element = new ElementType[SeqStackMaxSize];

	Stack.Size = zero;

	Stack.Auxiliary = { Stack.element };

}

void push_Stack(SeqStack& Stack, const ElementType& e){
	
	const bool FullStack = fullStack(Stack);
	if (!FullStack) {
		
		*Stack.Auxiliary.back = e;
		++Stack.Auxiliary.back;
		++Stack.Size;
	}

}

ElementType& TopStack(SeqStack& Stack){
	

	const bool EmptyQueue = emptyStack(Stack);

	ElementType* &Back =-- Stack.Auxiliary.back ;
	if (EmptyQueue) {
		terminate();
	}

	return*Back;
}

bool fullStack(const SeqStack& Stack){

	return Stack.Size == SeqStackMaxSize;
}

bool emptyStack(const SeqStack& Stack){

	return  !Stack.Size;
}

void pop_Stack(SeqStack& Stack){
	const bool EmptyQueue = emptyStack(Stack);
	size_t& size = Stack.Size;
	const ElementType* full = Stack.element + SeqStackMaxSize;

	if (!EmptyQueue) {

		if (Stack.Auxiliary.back == full) {
			terminate();
		}
		--size;
		return;
	}

	terminate();
}

const size_t& StackSize(const SeqStack& Stack){

	return Stack.Size;
}

void destroyStack(SeqStack& Stack){

	delete[] Stack.element;
	Stack.element = nullptr;
	Stack.Size = zero;
	Stack.Auxiliary = {};
}

链式栈

链式栈以链表基础之上维护一个队列统称为:“链式栈”
如图:

可以看到链式栈是头部插入头部删除. -极简的方式
当然也可以从尾部插入,尾部删除 但需要找到尾部的前驱结点 然后让他的下一个指向尾部的下一个
效率大大的下降 所以采用头部插入头部删除
当然也有双向的的实现

链式栈声明

//元素类型
using ElementType = use defined;

using  LinkListNode = struct _LinkListNode;

struct _LinkListNode {

	ElementType value;
	LinkListNode* next;
};

//链式栈辅助
struct _ListStackAuxiliary {

	LinkListNode* back;
};

using  ListStackAuxiliary = struct _ListStackAuxiliary;

//链式栈
struct _ListStack {

	LinkListNode* List;
	size_t size;
	ListStackAuxiliary Auxiliary;
};

//链式栈
using  ListStack = struct  _ListStack;

//最大的链式栈元素大小
const size_t ListStackMaxSize = 1000;

链式栈 操作算法声明

//初始化链式栈
void initStack(ListStack& Stack);

//入栈
void push_Stack(ListStack& Stack, const ElementType& value);

//访问栈顶元素
ElementType& TopStack(ListStack& Stack);

//链式栈已满
bool fullStack(const ListStack& Stack);

//链式栈已空
bool emptyStack(const ListStack& Stack);

//出栈
void pop_Stack(ListStack& Stack);

//栈元素大小
const size_t& StackSize(const ListStack& Stack);

//销毁链式栈
void destroyStack(ListStack& Stack);

链式栈 操作算法实现

#include"ListStack.h"
#include

const size_t zero = 0;

LinkListNode* creatorLinkNode(LinkListNode* where = nullptr) {

	LinkListNode* newNode = new LinkListNode;

	newNode->next = where;
	return newNode;
}

LinkListNode* creatorLinkNode(const ElementType& value, LinkListNode* where = nullptr) {

	LinkListNode* newNode = new LinkListNode;
	newNode->value = value;
	newNode->next = where;
	return newNode;
}

void initStack(ListStack& Stack) {

	Stack.List = new LinkListNode;
	Stack.List->next = nullptr;
	Stack. size = zero;
	Stack.Auxiliary = { Stack.List };
}

void Link(LinkListNode*& node, LinkListNode* const &  newnode) {

	if (node->next) {
		newnode->next = node->next;
	}
	node->next = newnode;
}


void LinkListInsert_froot(LinkListNode*& List, const ElementType& value) {

	LinkListNode* const newNode = creatorLinkNode(value);
	Link(List, newNode);
}

void unLink(LinkListNode*& node, LinkListNode*& DeleteNode) {

	if (node) {
		node->next = DeleteNode->next;
	}
}



void push_Stack(ListStack& Stack, const ElementType&value) {

	const bool FullStack = fullStack(Stack);
	LinkListNode*& back = Stack.Auxiliary.back;
	size_t& size = Stack.size;
	if (!FullStack){

		LinkListInsert_froot(back, value);
		++size;
	}


}


ElementType& TopStack(ListStack& Stack) {

	const bool EmptyStack = emptyStack(Stack);
	LinkListNode*& back = Stack.Auxiliary.back->next;
		
	if (EmptyStack) {
	 	destroyStack(Stack);
		std::terminate();
	}
	return back->value;
}


bool fullStack(const ListStack& Stack) {
	
	return Stack.size == ListStackMaxSize;
}


bool emptyStack(const ListStack& Stack) {
	return Stack.size == zero;
}


void pop_Stack(ListStack& Stack) {

	const bool EmptyStack = emptyStack(Stack);
	LinkListNode*& back = Stack.Auxiliary.back;
	if (!EmptyStack) {

		LinkListNode* deleteNode = back->next;
		unLink(back,deleteNode);
		delete deleteNode;
		--Stack.size;
	}
}


const size_t& StackSize(const ListStack& Stack) {

	return Stack.size;
}


void destroyStack(ListStack& Stack) {

	LinkListNode*& List = Stack.List;
	while (List) {
		LinkListNode* next = List->next;
		delete List;
		List = next;
	}
}

双向链式栈声明

//元素类型
using ElementType = use defined;

using  LinkListNode = struct _LinkListNode;

struct _LinkListNode {

	ElementType value;
	LinkListNode* prev;
	LinkListNode* next;
 };

//链式栈辅助
struct _ListStackAuxiliary {

	LinkListNode* back;
};

链式栈辅助
using  ListStackAuxiliary = struct _ListStackAuxiliary;

//链式栈
struct _ListStack {
	
	LinkListNode* List;
	size_t size;
	ListStackAuxiliary Auxiliary;	
};

using  ListStack = struct  _ListStack;

//最大的链式栈元素大小
const size_t ListStackMaxSize = 1000;

双向链式栈 操作算法声明

//初始化链式栈
void initStack(ListStack& Stack);

//入栈
void push_Stack(ListStack& Stack, const ElementType& value);

//访问栈顶元素
ElementType& TopStack(ListStack& Stack);

//链式栈已满
bool fullStack(const ListStack& Stack);

//链式栈已空
bool emptyStack(const ListStack& Stack);

//出栈
void pop_Stack(ListStack& Stack);

//栈元素大小
const size_t& StackSize(const ListStack& Stack);

//销毁链式栈
void destroyStack(ListStack& Stack);

双向链式栈 操作算法实现

#include "ListStack.h"
#include

const size_t zero = 0u;


LinkListNode* creatorLinkNode(LinkListNode* where = nullptr){

	LinkListNode* newNode = new LinkListNode;

	newNode->next = where;
	newNode->prev = where;
	return newNode;
}

LinkListNode* creatorLinkNode(const ElementType& value, LinkListNode* where = nullptr) {

	LinkListNode* newNode = new LinkListNode;
	newNode->value = value;
	newNode->next = where;
	newNode->prev = where;
	return newNode;
}

void initStack(ListStack& Stack){

	LinkListNode* & List=Stack.List = creatorLinkNode();
	Stack.size = zero;

	Stack.Auxiliary = { List };
}

void Link(LinkListNode*& node, LinkListNode*& newnode) {

	if (node->next) {

		node->next->prev = newnode;
		newnode->next = node->next;
	}
	newnode->prev = node;
	node->next = newnode;
}


void LinkListInsert_back(LinkListNode*& Where, const ElementType& value) {

	LinkListNode* Newnode = creatorLinkNode(value);
	Link(Where, Newnode);
	Where = Newnode;
}

void push_Stack(ListStack& Stack, const ElementType& value){

	const bool FullStack = fullStack(Stack);
	LinkListNode*& back = Stack.Auxiliary.back;
	size_t &size= Stack.size;

	if (!FullStack){
		LinkListInsert_back(back,value);
		++size;
	}

}

ElementType& TopStack(ListStack& Stack){

	const bool EmptyStack = emptyStack(Stack);

	LinkListNode*& Back = Stack.Auxiliary.back;
	if (EmptyStack) {

		destroyStack(Stack);
		std::terminate();
	}
	
	return Back->value;
}

bool fullStack(const ListStack& Stack){
	return Stack.size == ListStackMaxSize;
}

bool emptyStack(const ListStack& Stack){

	return! Stack.size;
}

void unLink(LinkListNode*& DeleteNode) {
	if (DeleteNode) {
		DeleteNode->prev->next = DeleteNode->next;

		if (DeleteNode->next) {
			DeleteNode->next->prev = DeleteNode->prev;
		}
	}
}


void pop_Stack(ListStack& Stack){

	const bool EmptyStack = emptyStack(Stack);
	LinkListNode*& Back = Stack.Auxiliary.back;
	if (!EmptyStack){

		LinkListNode* deleteNode = Stack.Auxiliary.back;
		Back = Back->prev;
		unLink(  deleteNode);
		delete deleteNode;
		--Stack.size;
	}

}

const size_t& StackSize(const ListStack& Stack)
{
	return Stack.size;
}

void destroyStack(ListStack& Stack) {

	LinkListNode*& List = Stack.List;
	while (List) {
		LinkListNode* next = List->next;
		delete List;
		List = next;
	}
	Stack = {};
}