聊一下:数据结构中的各种常见的树——AVL树、红黑树、B树、B+树
数据结构——树
- 常见的树
-
- 无序树
- 有序树
- 二叉树
- 满二叉树
- 完全二叉树
- 哈夫曼树
- AVL树
-
- AVL树的结构
- AVL树的特点
- AVL树的应用
- 红黑树
-
- 红黑树的结构
- 红黑树的特点
- 红黑树的应用
- 红黑树与AVL树的区别
- B-树
-
- B-树的结构
- B-树的特点
- B-树的应用
- B+树
-
- B+树的结构
- B+树的特点
- B+树的应用
- B-树与B+树的区别
- 有关树的一些问题
-
- 为什么文件系统要用B-树或B+树而不用二叉查找树?为什么不用hash?
- 为什么MySQL数据库索引使用B+树而不用B树?为什么不用hash?为什么不使用红黑树?
- 为什么JDK 1.8中Hashmap要使用红黑树?为什么不用B树?为什么不用B+树?为什么不使用AVL树?为什么不用hash?
- 为什么MongoDB采用B树索引,而Mysql用B+树做索引?
常见的树
今天我们来聊一下在数据结构中,几种应用比较广泛,并且十分最重要的树型结构,本文是基于对树的基本结构与特征有了一定了解之后而撰写的文章。如果对树的基本结构不太了解的同学,推荐看一下《java数据结构和算法》。百度云链接:数据结构和算法
本文主要介绍AVL树、红黑树、B树、B+树的结构,以及在其应用。并通过横向比较来展示各种数据结构的优点与缺点。
无序树
树的任意节点的子节点没有顺序关系。
有序树
树的任意节点的子节点有顺序关系。
二叉树
二叉树是数据结构中一种重要的数据结构,也是树结构中最基础的结构。
二叉树的定义:二叉树的每个结点至多只有二棵子树(不存在度大于2的结点),二叉树的子树有左右之分,次序不能颠倒。二叉树的第i层至多有2i-1个结点;深度为k的二叉树至多有2k-1个结点;对任何一棵二叉树T,如果其终端结点数为n0,度为2的结点数为n2,则n0=n2+1。
满二叉树
满二叉树: 叶子节点都在同一层并且除叶子节点外的所有节点都有两个子节点。
满二叉树的性质:
1) 一颗树深度为h,最大层数为k,深度与最大层数相同,k=h;
2) 叶子数为2h;
3) 第k层的结点数是:2k-1;
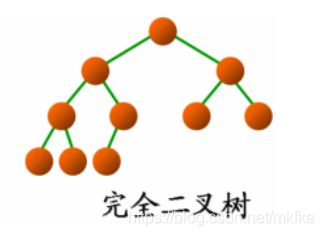
完全二叉树
若设二叉树的深度为h,除第 h 层外,其它各层 (1~(h-1)层) 的结点数都达到最大个数,第h层所有的结点都连续集中在最左边,这就是完全二叉树。
哈夫曼树
带权路径最短的二叉树称为哈夫曼树或最优二叉树。
AVL树
AVL树的结构
平衡二叉搜索树(Self-balancing binary search tree)又被称为AVL树,且具有以下性质:它是一 棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。
AVL树的特点
AVL树是带有平衡条件的二叉查找树,一般是用平衡因子差值判断是否平衡并通过旋转来实现平衡,左右子树树高不超过1,和红黑树相比,AVL树是严格的平衡二叉树,平衡条件必须满足(所有节点的左右子树高度差不超过1)。不管我们是执行插入还是删除操作,只要不满足上面的条件,就要通过旋转来保持平衡,而旋转是十分耗时的,AVL树适合用于插入与删除次数比较少,但查找多的情况。
二叉查找树中结点的插入与删除等操作的时间复杂度都是O(h),其中h为查找树的高度。由于AVL树的高度为logn,有如下结论:在AVL树中删除一个结点后,之多需要O(logn)次旋转即可使之平衡。由于在AVL树中按通常查找树的方法删除结点需要O(logn)时间,平衡调整也需要O(logn)时间,因此在AVL树中删除结点的操作可以在O(logn)时间内完成。
AVL树的应用
1、Windows NT内核中广泛存在。
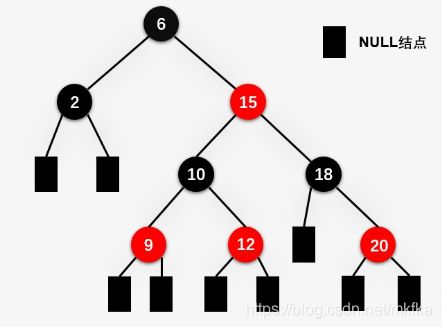
红黑树
红黑树也是一种二叉查找树,红黑树每一个结点都增加一个存储位,用来表示结点的颜色,可以是红或黑。通过对对任何一条从根到叶子的路径上各个结点着色的方式的限制,红黑树确保没有一条路径会比其他路径长两倍,因此,红黑树是一种弱平衡树。 对于要求严格的AVL树来说,它为了保持平衡旋转的次数较少,所以,对于搜索、插入、删除操作较多的情况下,红黑树的综合能力较好。
红黑树的结构
红黑树的特点
红黑树是一种含有红黑结点并能自平衡的二叉查找树。它必须满足下面性质:
-
性质1:每个结点要么是红色,要么是黑色
-
性质2:根节点是黑色
-
性质3:叶子结点都是黑色
-
性质4:每个红色结点的子结点一定都是黑色
-
性质5:任意一个结点到每个叶子结点的路径包含数量相同的黑色结点。
红黑树的应用
1、广泛用于C ++的STL中
2、著名的Linux的的进程调度完全公平调度程序,用红黑树管理进程控制块,进程的虚拟内存区域都存储在一颗红黑树上,每个虚拟地址区域都对应红黑树的一个节点,左指针指向相邻的地址虚拟存储区域,右指针指向相邻的高地址虚拟地址空间;
3、IO多路复用的epoll的实现采用红黑树组织管理的的的sockfd,以支持快速的增删改查;
4、Nginx的的的中用红黑树管理定时器,因为红黑树是有序的,可以很快的得到距离当前最小的定时器;
5、Java中TreeMap、TreeSet、JDK1.8 HashMap的实现;
红黑树与AVL树的区别
1、红黑树不追求“完全平衡”,即不像AVL树那样要求平衡因子小于1,红黑树用非严格的平衡来换取旋转次数的降低,任何不平衡都会在三次旋转之内解决,而AVL树的旋转的量级为O(logn)。
2、AVL树的结构相较于红黑树更为平衡,插入和删除引起失衡,红黑树恢复平衡效率更高;当然,由于AVL高度平衡,因此AVL的查询效率更高。
总结: 红黑树是一种弱平衡二叉搜索树(红黑树确保没有一条路径比其它路径长出两倍),由于是弱平衡,可以看出,在相同的节点情况下,AVL树的高度低于红黑树,相对于要求严格的AVL树来说,它的旋转次数少,所以对于插入与删除较多的情况,我们就用红黑树。
B-树
一般的,在分级存储系统中,各级存储器的速度有着巨大的差异,以磁盘和内存为例,前者平均访问速度为10ms左右,而内存储器的平均访问时间为ns级。因此,为了节省一次外存储器的访问,我们宁愿多访问内存储器一百次、一千次、甚至一万次。当数据规模太大时,以至于内存储器无法容纳时,即使前面介绍的AVL树,在时间上也会大打折扣。 于是就引入了B-树。
B-树的结构
B-树作为一种多路搜索树,所谓的m阶B-树即满足如下特性的m叉树:

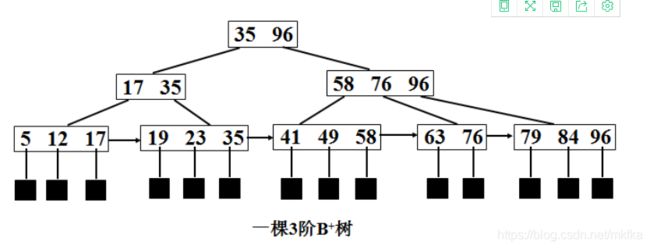
下面为一棵3阶B-数:
在实际应用中的B树的阶数m都非常大(通常大于100),所以即使存储大量的数据,B树的高度仍然比较小。每个结点中存储了关键字(key)和关键字对应的数据(data),以及孩子结点的指针。
B-树的特点
正如前面所指出的,B-树的查找适合于大规模的数据。实际的做法是,将大量数据组织为一棵B-树,并存于外存储器,B-树的根节点常驻内存。一旦需要查找,则按上述过程,首先将根节点作为当前结点,在当前结点中顺序查找;如果当前结点不存在需要查找的关键字,则根据相应的引用,找到外存中的某一个结点,将其读入内存,作为新的当前结点继续查找。如此进行下去,直到找到相应的关键字或查找失败。
由此可见,在B-树中进行查找所需要的时间,无外乎两类操作的时间消耗:一种是,在B-树上找结点,即将外存中的结点读入内存;另一种是,在结点中找关键字。在前面也提到,内外存储器的平均访问时间存在巨大差异,所以这两部分时间中,前者必然是主要部分。因为,B-树的查找效率取决于外存的访问次数。
B-树的应用
1、B-主要应用在文件系统中。
2、部分数据库索引(MongoDB)
B+树
B+树的结构
m阶B+树是m阶B-tree的变体,它的定义大致跟B-tree一致,不过有以下几点不同:
1、有n棵子树的结点中含有n个关键字,每个关键字不保存数据,只用来索引,所有数据都保存在叶子节点,其中⌈m/2⌉ <= n <= m
2、所有的叶子结点中包含了全部关键字的信息,及指向含这些关键字记录的指针,且叶子结点本身依关键字的大小自小而大顺序链接
3、所有的非终端结点可以看成是索引部分,结点中仅含其子树(根结点)中的最大(或最小)关键字
4、通常在B+树上有两个头指针,一个指向根结点,一个指向关键字最小的叶子结点
B+树的特点
1、B+树磁盘读写代价更低
B+树的非叶子结点里面没有数据。所以内部节点较小,相同内存所能容纳的关键字数量也越多,一次性读入内存的中需要查找的关键字也就越多,相对来说IO读写次数就降低了。
2、B+树的查询效率更加稳定
非终结点并不是最终指向文件内容的结点,而只是叶子结点中关键字的索引。所以任何关键字的查找必须走一条从根结点到叶子结点的路。所有关键字查询的路径长度相同,导致每一个数据的查询效率相当。
3、B+树可以范围查询,遍历所有的数据更方便
B+树只要遍历叶子节点就可以实现整棵树的遍历,而其他的树形结构 要中序遍历才可以访问所有的数据。
B+树的应用
1、B+树被广泛应用在数据库的索引中
2、操作系统的文件系统
B-树与B+树的区别
1、结构上的区别
2、查询效率的区别
有关树的一些问题
为什么文件系统要用B-树或B+树而不用二叉查找树?为什么不用hash?
在把磁盘里的数据加载到内存中的时候,是以页为单位来加载的,节点与节点之间的数据是不连续的,所以不同的节点,很有可能分布在不同的磁盘页中。
而实际上磁盘的寻址加载是最耗时的。实际上磁盘的加载次数,基本上是和树的高度相关联的,高度越高,加载次数越多,越矮,加载次数越少。所以对于这种文件索引的存储,我们一般会选择矮胖的树形结构。而二叉树的由于每个结点最多只有两个子节点,树的高度太高,很显然效率并不高。
为什么不用hash?
当数据量很大时,hash的缺点也会体现突出,太耗内存了!!!并且还会产生hash冲突。
为什么MySQL数据库索引使用B+树而不用B树?为什么不用hash?为什么不使用红黑树?
为什么不使用红黑树?
Mysql数据库的索引是保存在磁盘中,所以像红黑树这种二叉查找树由于高度太高,寻址次数太多,影响效率,直接pass。
为什么不用hash?
哈希表则不能范围查询。
为什么不用B树而用B+?
1、B树对于范围查询的效率太低了。B+树只需要去遍历叶子节点就可以实现整棵树的遍历。
2、B+树的磁盘读写代价更低,B+树的内部节点并没有指向关键字具体信息的指针,因此其内部节点相对B树更小,如果把所有同一内部节点的关键字存放在同一盘块中,那么盘块所能容纳的关键字数量也越多,一次性读入内存的需要查找的关键字也就越多,相对IO读写次数就降低了。
3、B+树的查询效率更加稳定:由于非终结点并不是最终指向文件内容的结点,而只是叶子结点中关键字的索引。所以任何关键字的查找必须走一条从根结点到叶子结点的路。所有关键字查询的路径长度相同,导致每一个数据的查询效率相当。
为什么JDK 1.8中Hashmap要使用红黑树?为什么不用B树?为什么不用B+树?为什么不使用AVL树?为什么不用hash?
jdk1.7中的HashMap本来是数组+链表的形式,链表由于其查找慢的特点,所以需要被查找效率更高的树结构来替换。
为什么不用B、B+树?
如果用B树、B+树的话,在数据量不是很多的情况下(发生hash冲突的结点才会被放在链表中,所有数据量不会特别大),数据都会“挤在”一个结点里面。这个时候遍历效率就退化成了链表。
为什么不使用AVL树呢?
AVL的查询效率固然比红黑树好,但是对于hashmap集合是经常需要进行增删操作的,红黑树增删性能比AVL好(红黑树恢复平衡只需最多三次旋转,而AVL需要logn次),肯定是选择使用综合性能较好的红黑树啦。
为什么不使用hash?
hash的查找速度比红黑树要快,属于常数级别;而红黑树的查找速度是log(n)。红黑树占用的内存更小(仅需要为其存在的节点分配内存),而Hash事先应该分配足够的内存存储散列表,即使有些槽可能弃用。主要还是内存的原因吧,如果使用hash,那没一个有hash冲突的地方都要创建一个hash表,比较占内存。
为什么使用红黑树?
红黑树增删查效率均为logn,恢复平衡最多只需三次旋转。
为什么MongoDB采用B树索引,而Mysql用B+树做索引?
由于关系型数据库和非关系型数据的设计方式上的不同。导致在关系型数据中,遍历操作比较常见,因此采用B+树作为索引,比较合适。而在非关系型数据库中,单一查询比较常见,因此采用B树作为索引,比较合适。