深度学习之目标检测模型后处理(非极大值抑制与WBF)
Non-Maximum Suppression(NMS)非极大值抑制。从字面意思理解,抑制那些非极大值的元素,保留极大值元素。其主要用于目标检测,目标跟踪,3D重建,数据挖掘等。
目前NMS常用的有标准NMS, Soft NMS, DIOU NMS等。后续出现了新的Softer NMS,Weighted NMS等改进版。
一、原始NMS
以目标检测为例,目标检测推理过程中会产生很多检测框(A,B,C,D,E,F等),其中很多检测框都是检测同一个目标,但最终每个目标只需要一个检测框,NMS选择那个得分最高的检测框(假设是C),再将C与剩余框计算相应的IOU值,当IOU值超过所设定的阈值(普遍设置为0.5,目标检测中常设置为0.7,仅供参考),即对超过阈值的框进行抑制,抑制的做法是将检测框的得分设置为0,如此一轮过后,在剩下检测框中继续寻找得分最高的,再抑制与之IOU超过阈值的框,直到最后会保留几乎没有重叠的框。这样基本可以做到每个目标只剩下一个检测框。
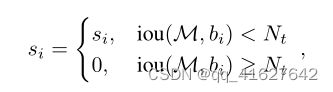
1、 斜框的nms实现代码
def py_cpu_soft_nms_poly(dets, thresh):
scores = dets[:, 8]
polys = []
areas = []
# for i in range(len(dets)):
for i in range(dets.shape[0]):
tm_polygon = shgeo.Polygon([(dets[i][0], dets[i][1]),
(dets[i][2], dets[i][3]),
(dets[i][4], dets[i][5]),
(dets[i][6], dets[i][7])])
polys.append(tm_polygon)
order = scores.argsort()[::-1]#检测置信度进行由大到小排序
keep = []
while order.size > 0:
ovr = []
i = order[0]
keep.append(i)#添加最大置信度得分框的索引
for j in range(order.size - 1):
# iou = polyiou.iou_poly(polys[i], polys[order[j + 1]])
iou = cal_iou(polys[i], polys[order[j + 1]]) #计算最大置信度得分框与后续框的iou
ovr.append(iou)
ovr = np.array(ovr)
# print('ovr: ', ovr)
# print('thresh: ', thresh)
try:
if math.isnan(ovr[0]):
pdb.set_trace()
except:
pass
inds = np.where(ovr <= thresh)[0]#保留小于域值的框
# print('inds: ', inds)
order = order[inds + 1]#保留的框索引
return keep
2、 正框的nms实现代码
def nms_float_fast(dets, scores, thresh):
"""
# It's different from original nms because we have float coordinates on range [0; 1]
:param dets: numpy array of boxes with shape: (N, 5). Order: x1, y1, x2, y2, score. All variables in range [0; 1]
:param thresh: IoU value for boxes
:return: index of boxes to keep
"""
x1 = dets[:, 0]
y1 = dets[:, 1]
x2 = dets[:, 2]
y2 = dets[:, 3]
areas = (x2 - x1) * (y2 - y1)
order = scores.argsort()[::-1]
keep = []
while order.size > 0:
i = order[0]
keep.append(i)
xx1 = np.maximum(x1[i], x1[order[1:]])
yy1 = np.maximum(y1[i], y1[order[1:]])
xx2 = np.minimum(x2[i], x2[order[1:]])
yy2 = np.minimum(y2[i], y2[order[1:]])
w = np.maximum(0.0, xx2 - xx1)
h = np.maximum(0.0, yy2 - yy1)
inter = w * h
ovr = inter / (areas[i] + areas[order[1:]] - inter)
inds = np.where(ovr <= thresh)[0]
order = order[inds + 1]
return keep
二、NMS的缺点
-
需要手动设置IOU阈值,阈值的设置会直接影响重叠目标的检测,太大造成误检,太小达不到理想情况。
(在NMS方法中,如果这些盒子的重叠、交叉-过并(IoU)高于某个阈值,就认为它们属于一个对象。因此,盒子过滤过程依赖于这一单一IoU阈值的选取,影响模型的性能。然而,设置这个阈值是棘手的:如果有并排的对象,其中一个将被消除。图[1显示了这样一个例子。对于IoU阈值为0.5,将只剩下一个盒子预测。检测到的其他重叠对象将被删除。这种误差降低了模型的精度。)
图1:这张照片展示了比赛中几匹重叠的马。对于几个具有高置信度得分的检测,对于IoU阈值高于0.5,NMS算法只会选择一个检测。

-
高于阈值的直接设置score为0,做法太hard。
-
只能在CPU上运行,成为影响速度的重要因素。
-
通过IoU来评估,IoU的做法对目标框尺度和距离的影响不同。
三、NMS的改进思路
-
根据手动设置阈值的缺陷,通过自适应的方法在目标系数时使用小阈值,目标稠密时使用大阈值。例如Adaptive NMS
-
将高于阈值的直接置为0的做法太hard,通过将其根据IoU大小来进行惩罚衰减,则变得更加soft。例如Soft NMS,Softer NMS。
-
只能在CPU上运行,速度太慢的改进思路有三个,一个是设计在GPU上的NMS,如CUDA NMS,一个是设计更快的NMS,如Fast NMS,最后一个是掀桌子,设计一个神经网络来实现NMS,如ConvNMS。
-
IoU的做法存在一定缺陷,改进思路是将目标尺度、距离引进IoU的考虑中。如DIoU。
四、Soft NMS
根据前面对目标检测中NMS的算法描述,易得出标准NMS容易出现的几个问题:当阈值过小时,如下图所示,绿色框容易被抑制;当过大时,容易造成误检,即抑制效果不明显。因此,出现升级版soft NMS。
衰减与M有重叠的其他检测盒的分数似乎是一种有希望改善NMS的方法。同样清楚的是,与M具有较高重叠的检测框的分数应该衰减得更多,因为它们具有更高的假阳性可能性。因此,我们建议用以下规则更新修剪步骤.
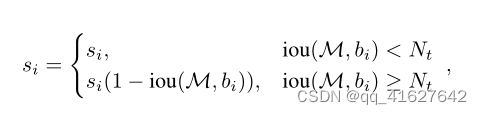
上述函数会将阈值NTA以上的检测分数衰减为与M重叠的线性函数。因此,远离M的检测框不会受到影响,而非常接近的检测框将被分配更大的惩罚。
1、 斜框的soft-nms实现代码
def cpu_soft_nms_float(dets, iou_thr=0.5, sigma=0.5, thresh=0.001, weights=None, method=2):
"""
:param dets boxes:
list of boxes predictions from each model, each box is 9 numbers. Order of boxes: x1, y1, x2, y2,x3,y3,x4,y4,scores.
:param iou_thr: IoU value for boxes to be a match.
:param sigma: Sigma value for SoftNMS
:param thresh: threshold for boxes to keep (important for SoftNMS)
:param weights: list of weights for each model. Default: None, which means weight == 1 for each model
:param method: 1 - linear soft-NMS, 2 - gaussian soft-NMS, 3 - standard NMS
:return: boxes: boxes coordinates (Order of boxes: x1, y1, x2, y2).
:return: scores: confidence scores
:return: labels: boxes labels
Based on: https://github.com/DocF/Soft-NMS/blob/master/soft_nms.py
It's different from original soft-NMS because we have float coordinates on range [0; 1]
"""
N = dets.shape[0]
bboxs=dets[:, 0:8]
scores = dets[:, 8]
#dets boxes是两个模型推理结果的合并,每个模型的权重为1,1.
if weights is None:
scores= (np.array(scores) * 1) / 2
indexes = np.array([np.arange(N)])
bboxs = np.concatenate((bboxs, indexes.T), axis=1)
areas = []
for j in range(N):
tm_polygon = shgeo.Polygon([(bboxs[j][0], bboxs[j][1]),
(bboxs[j][2], bboxs[j][3]),
(bboxs[j][4], bboxs[j][5]),
(bboxs[j][6], bboxs[j][7])])
tm_polygon_area = tm_polygon.area
areas.append(tm_polygon_area)
for i in range(N):
# intermediate parameters for later parameters exchange
tBD = bboxs[i, :].copy()
tscore = scores[i].copy()
tarea = np.array(areas)[i].copy()
pos = i + 1
#
if i != N - 1:
maxscore = np.max(scores[pos:], axis=0) #检索pos后面的最大的分
maxpos = np.argmax(scores[pos:], axis=0)#检索pos后面的最大的分的索引
else:
maxscore = scores[-1]
maxpos = 0
#小于最大得分的进行值的替换
if tscore < maxscore:
bboxs[i, :] = bboxs[maxpos + i + 1, :]
bboxs[maxpos + i + 1, :] = tBD
tBD = bboxs[i, :]
scores[i] = scores[maxpos + i + 1]
scores[maxpos + i + 1] = tscore
tscore = scores[i]
areas[i] = areas[maxpos + i + 1]
areas[maxpos + i + 1] = tarea
tarea = areas[i]
# IoU calculate,计算dets[i]与后续dets[pos:]框的IOU
ovr=[]
for j in range(pos,N,1):
# iou = polyiou.iou_poly(polys[i], polys[order[j + 1]])
poly1=shgeo.Polygon([(bboxs[i][0], bboxs[i][1]),
(bboxs[i][2], bboxs[i][3]),
(bboxs[i][4], bboxs[i][5]),
(bboxs[i][6], bboxs[i][7])])
poly2=shgeo.Polygon([(bboxs[j][0], bboxs[j][1]),
(bboxs[j][2], bboxs[j][3]),
(bboxs[j][4], bboxs[j][5]),
(bboxs[j][6], bboxs[j][7])])
iou = cal_iou(poly1, poly2)
ovr.append(iou)
ovr = np.array(ovr)
# Three methods: 1.linear 2.gaussian 3.original NMS
if method == 1: # linear
weight = np.ones(ovr.shape)
weight[ovr > iou_thr] = weight[ovr >iou_thr] - ovr[ovr > iou_thr]
elif method == 2: # gaussian
weight = np.exp(-(ovr * ovr) / sigma)
else: # original NMS
weight = np.ones(ovr.shape)
weight[ovr > iou_thr] = 0
scores[pos:] = weight * scores[pos:]#对pos后面的置信度得分进行衰减
# select the boxes and keep the corresponding indexes
inds = bboxs[:, 8][scores > thresh]#保留scores大于阈值的框
keep = inds.astype(int)
return keep
1、 正框的soft-nms实现代码
def cpu_soft_nms_float(dets, sc, Nt, sigma, thresh, method):
"""
Based on: https://github.com/DocF/Soft-NMS/blob/master/soft_nms.py
It's different from original soft-NMS because we have float coordinates on range [0; 1]
:param dets: boxes format [x1, y1, x2, y2]
:param sc: scores for boxes
:param Nt: required iou
:param sigma:
:param thresh:
:param method: 1 - linear soft-NMS, 2 - gaussian soft-NMS, 3 - standard NMS
:return: index of boxes to keep
"""
# indexes concatenate boxes with the last column
N = dets.shape[0]
indexes = np.array([np.arange(N)])
dets = np.concatenate((dets, indexes.T), axis=1)
# the order of boxes coordinate is [y1, x1, y2, x2]
y1 = dets[:, 1]
x1 = dets[:, 0]
y2 = dets[:, 3]
x2 = dets[:, 2]
scores = sc
areas = (x2 - x1) * (y2 - y1)
for i in range(N):
# intermediate parameters for later parameters exchange
tBD = dets[i, :].copy()
tscore = scores[i].copy()
tarea = areas[i].copy()
pos = i + 1
#
if i != N - 1:
maxscore = np.max(scores[pos:], axis=0)
maxpos = np.argmax(scores[pos:], axis=0)
else:
maxscore = scores[-1]
maxpos = 0
if tscore < maxscore:
dets[i, :] = dets[maxpos + i + 1, :]
dets[maxpos + i + 1, :] = tBD
tBD = dets[i, :]
scores[i] = scores[maxpos + i + 1]
scores[maxpos + i + 1] = tscore
tscore = scores[i]
areas[i] = areas[maxpos + i + 1]
areas[maxpos + i + 1] = tarea
tarea = areas[i]
# IoU calculate
xx1 = np.maximum(dets[i, 1], dets[pos:, 1])
yy1 = np.maximum(dets[i, 0], dets[pos:, 0])
xx2 = np.minimum(dets[i, 3], dets[pos:, 3])
yy2 = np.minimum(dets[i, 2], dets[pos:, 2])
w = np.maximum(0.0, xx2 - xx1)
h = np.maximum(0.0, yy2 - yy1)
inter = w * h
ovr = inter / (areas[i] + areas[pos:] - inter)
# Three methods: 1.linear 2.gaussian 3.original NMS
if method == 1: # linear
weight = np.ones(ovr.shape)
weight[ovr > Nt] = weight[ovr > Nt] - ovr[ovr > Nt]
elif method == 2: # gaussian
weight = np.exp(-(ovr * ovr) / sigma)
else: # original NMS
weight = np.ones(ovr.shape)
weight[ovr > Nt] = 0
scores[pos:] = weight * scores[pos:]
# select the boxes and keep the corresponding indexes
inds = dets[:, 4][scores > thresh]
keep = inds.astype(int)
return keep
五、 总结NMS和Soft-NMS
这种方法在单一模型上运行良好。然而,它们只选择盒子,不能有效地产生由各种模型组合的预测的平均定位。模型集合广泛用于不需要实时推理的应用中。与单个模型相比,组合不同模型的预测可以更好地概括,通常会产生更准确的结果[。集成方法通常在机器学习竞赛中获得冠军.
六、WBF
WBF官网链接
1、WBF缺点
既然wbf要比nms效果更好,为什么用它的人却不多呢?
首先是推理速度,wbf处理预测框的速度是nms速度的三倍以上(我假设你明白了wbf是如何工作的,所以我也就不多解释为啥了);
其次是工作量,对于我这种小白来说,如果想要求得比nms更好的后处理算法,我会选择nms的一系列变种,比如diou-nms和ciou-nms,代码易实现,推理速度也不会太让人急挠的,wbf我就不知道该怎么去实现了,费劲巴拉的,效果还没那么好;
最后,wbf是在nms处理之后的模型上研究出来的。
2、如何正确使用WBF
优点和缺点都已经介绍完了,那么我们该如何使用这个算法。**在kaggle竞赛中,很多参赛者会使用wbf算法去处理多个模型的输出结果,使得处理之后的结果集百家之所长,达到从众多竞争对手中脱颖而出的效果。**所以个人认为,如果你是在参加竞赛,要求准确率而对实时性要求不高,你可以将多个模型的推理结果送入wbf中去处理,这会取得不错的效果。但是如果你要用于模型创新中,wbf的结果可能会让你失望,我会推荐你选择nms的一系列变种,而不是使用wbf算法。
这个 WBF 算法可以直接用来代替 NMS,不过计算量可能会大一点。
对于一张图片,可以用多个不同的模型来做预测,然后对所有预测结果运用 WBF 算法,得到 1 个结果。作者说这个结果可能好过单个模型的预测结果。作者提出 WBF 算法也是主要应用于这种场景。
如果只有 1 个模型,也可以用 WBF 算法。方法就是把得分阈值设低一点,让网络输出一堆框框,然后对这些框做 WBF。如果网络判别能力强,得分低的框往往是一些垃圾框,它在融合过程中也没什么权重,所以直接做 WBF 应该没有问题。
⑧ 模型融合时采用多种结构的Backbone进行融合(Swin + ReResNet + ResNeXt-DCN)。(做Backbone对比实验时发现,Swin尽管整体mAP最高,但是部分类别的AP要比一些CNN结构低好几个点,不同Backbone在不同类别上的AP表现区别也不小,所以同一算法采用不同Backbone进行融合的话应该会比我使用两种算法进行融合的效果要好。这里同样也是比赛后期时间不够没有进行尝试,融合的结果还是太少了,最终就融合了3\4种结果,感觉基于ROI Transformer训练一个尾部类别的检测器应该还能提1~2个点,但是它测试所需时间太久了,测试所花的时间成本太大)
⑨ 模型融合结果做NMS时可以更”Soft“一点 —— Weighted Boxes Fusion。(也是竞赛时发现的,两个算法做ensemble的时候,部分类别融合结果后的AP反而更低了,说明过于Hard的NMS错杀了一部分较低置信度的高质量预测框,采用WBF的方式替换NMS的话效果应该会更好)
3、WBF处理流程
加权框融合 WBF
