【数据库系统】数据库系统概论====第二章 关系数据库

第二章 关系数据库

---

前言

关系数据库简介
1970年IBM公司的E.F.Codd提出关系数据模型
1972年提出了关系的第一、第二、第三范式
1974年提出了关系的BC范式
80年代后，关系数据库系统成为最重要、最流行的数据库系统
典型实验系统：System R、University INGRES
典型商用系统：ORACLE、DB2、SYBASE、INGRES、INFORMIX

2.1关系数据结构及形式化定义

2.1.1关系

单一的数据结构–关系
现实世界的实体以及实体间的各种联系均用关系来表示
逻辑结构–二维表
从用户角度，关系模型中数据的逻辑结构是一张二维表，关系模型是建立在集合代数的基础上。

1. 域
   定义：域是一组具有相同数据类型的值的集合。
2. 笛卡尔积

• 定义：给定一组域$D_1$，$D_2$，…，$D_n$，这些域可以是相同的。$D_1$，$D_2$，…，$D_n$的笛卡尔积为：
  $D_1$×$D_2$×…×$D_n$={（$d_1$，$d_2$，…，$d_n$）|$d_i$∈$D_i$，i=1,2，…，n}。所有域的所有取值的一个组合。
• 元组：笛卡尔积中的每一个元素（$d_1$，$d_2$，…，$d_n$）称作一个n元组或简称元组。
• 分量：笛卡尔积元素（$d_1$，$d_2$，…，$d_n$）中的每一个值di称作一个分量。
• 基数：若Di（i=1,2，…，n）为有限集，其基数为mi（i=1,2，…，n），则$D_1$×$D_2$×…×$D_n$的基数M为：
  $$M=\prod _{i=1}^{n}mi$$
• 笛卡尔积的表示方法：笛卡尔积可表示为一个二维表，表中的每行对应一个元组，表中的每列对应一个域。
  $D_1$，$D_2$，…，$D_n$的笛卡尔积的子集不是都有实际含义，只有某个子集才有实际含义。

3. 关系

• 关系
  $D_1$×$D_2$×…×$D_n$的子集称作在域$D_1$，$D_2$，…，$D_n$上的关系，表示为R（$D_1$，$D_2$，…，$D_n$）。
  R表示关系名，n表示关系的目或度。
• 元组
  关系中的每个元素是关系中的元组，通常用t表示。
• 单元关系与二元关系
  当n=1时，称该关系为单元关系或一元关系。
  当n=2时，称 该关系为二元关系。
• 关系的表示
  关系也是一个二维表，表的每行对应一个元组，表的每列对应一个域，一个属性。
• 属性
  关系中不同列可以对应相同的域，为了加以区分，必须对每列起一个名字，称为属性。
  n目关系必有n个属性。
• 码
  候选码：若关系中的某一属性组的值能唯一地标识一个元组，则称该属性组为候选码。
  简单的情况：候选码只包含一个属性。
  全码：最极端的情况：关系模式的所有属性组是这个关系模式的候选码，称为全码。
  主码：若一个关系有多个候选码，则选定其中一个为主码。
  主属性：候选码的诸属性称为主属性。
  非主属性：不包含在任何候选码中的属性或非码属性。
• 三类关系
  ①基本关系（基本表或基表）：实际存在的表，是实际存储数据的逻辑表示。
  ②查询表：查询结果对应的表。
  ③视图表：由基本表或其他视图表导出的表，是虚表，不对应实际存储的数据。
• 基本关系的性质
  ①列是同质的。
  ②不同的列可出自同一个域，其中的每一列称为一个属性，不同的属性要给予不同的属性名。
  ③列的顺序无所谓，列的次序可以任意交换。
  ④任意两个元组的候选码不能相同。
  ⑤行的顺序无所谓，行的次序可以任意交换。
  ⑥分量必须取原子值，这是规范条件中最基本的一条。

2.1.2关系模式

1. 什么是关系模式
   关系模式是对关系的描述。关系模式是型，关系是值。

• 元组集合的结构
  属性构成、属性来自的域、属性与域之间的映像关系。
• 一个关系通常由赋予它的元组语义确定。
• 现实的世界中还存在着完整性约束。

2. 定义关系模式
   关系模式可以形式化地表示为：R（U，D，DOM，F）
   R：关系名
   U：组成该关系的属性名集合
   D：属性组U中属性所来自的域
   DOM：属性向域的映像集合
   F：属性间的数据依赖关系集合
3. 关系模式与关系

• 关系模式是静态的、稳定的。
• 关系是动态的、随时间不断变化的。
• 关系是关系模式在某一时刻的状态或内容，在实际工作中关系模式和关系往往统称为关系，需要通过上下文加以区别。

2.1.3关系数据库

1. 关系数据库
   在一个给定的应用领域中，所有关系的集合构成一个关系数据库。
2. 关系数据库的型与值

• 关系数据库的型：关系数据库模式，对关系数据库的描述。
• 关系数据库模式：若干域的定义，在这些域上定义的若干关系模式。
• 关系数据库的值：厝模式在某一时刻对应的关系的集合，简称为关系数据库。

2.1.4关系模型的存储结构

1. 有的关系数据库管理系统中一个表对应一个操作系统文件，将物理数据组织交给操作系统完成。
2. 有的关系数据库管理系统从操作系统那里申请若干个大的文件，自己划分文件空间组织表、索引表等存储结构，并进行存储管理。

2.2关系数据结构

2.2.1基本关系操作

1. 常用的关系操作

• 查询：选择、投影、连接、除、并、交、差等，其中：选择、投影、并、差、笛卡尔积是5种基本操作。
• 数据更新：插入、删除、修改。
  查询的表达能力是其中最主要的部分。

2. 关系操作的特点
   集合操作方式：操作的对象和结果都是集合，一次一集合的方式。

2.2.2关系数据库语言的分类

1. 关系代数语言
   用对关系的运算来表达查询要求。代表：ISBL
2. 关系演算语言
   用谓词来表达查询要求。
   ①元组关系演算语言：谓词变元的基本对象是元组变量。代表：APLHA，QUEL
   ②域关系演算语言：谓词变元的基本对象是域变量。代表：QBE
3. 具有关系代数和关系演算双重特点的语言
   代表：SQL

2.3关系的完整性

关系模型中有三类完整性约束：实体完整性、参照完整性和用户定义完整性。
其中实体完整性、参照完整性是关系模型必须满足的完整性约束条件，成为关系的两个不变性，应该由关系系统自动支持。
用户定义的完整性是应用领域需要遵循的约束条件，体现了具体领域中的语义约束。

2.3.1实体完整性

实体完整性规则是指若属性A是基本关系R的主属性，则属性A不能取空值。
空值就是“不知道”或“不存在”或“无意义”的值。

实体完整性规则的说明：

• 实体完整性规则是针对基本关系而言的。一个基本表通常对应现实世界的一个实体集。
• 现实世界中的实体是可区分的，即它们具有某种唯一性标识。
• 关系模型中以主码作为唯一性标识。
• 主码中的属性即主属性不能取空值。
  主属性取空值，就说明存在某个不可标识的实体，即存在不可区分的实体，这与第2）点相矛盾，因此这个规则称为实体完整性。
  实体完整性规则规定基本关系的所有主属性都不能取空值。

2.3.2参照完整性

1. 关系间的引用
   在关系模型中实体及实体间的联系都是用关系来描述的，存在着关系与关系间的引用。
2. 外码

• 定义：设F是基本关系R的一个或一组属性，但不是关系R的码。如果F与基本关系S的主码Ks相对应，则称F是基本关系R的外码。
  基本关系R称为参照关系
  基本关系S称为被参照关系
  关系R和S不一定是不同的关系。
  目标关系S的主码Ks和参照关系的外码F必须定义在同一个（或一组）域上。
  外码并不一定要与相应的主码同名，当外码与相应的主码属于不同关系时，往往取相同的名字，以便于识别。

3. 参照完整性规则

• 参照完整性规则：若属性（或属性组）F是基本关系R的外码，它与基本关系S的主码Ks相对应（基本关系R和S不一定是不同的关系），则对于R中每个元组在F上的值必须为：
  或者取空值（F的每个属性值均为空值）；
  或者等于S中某个元组的主码值。

2.3.3用户定义的完整性

针对某一具体关系数据库的约束条件，反映某一具体应用所涉及的数据必须满足的语义要求。
关系模型应提供定义和检验这类完整性的机制，以便用统一的系统的方法处理它们，而不要由应用程序承担这一功能。

2.4关系代数

关系代数是一种抽象的查询语言，是对关系的运算来表达查询。
关系代数的运算对象是关系，运算结果也是关系。
关系代数按运算符的不同可分为传统的集合运算和专门的关系运算两类。
集合运算是从关系的水平方向进行的角度进行。
专门的关系运算不仅涉及行而且涉及列。

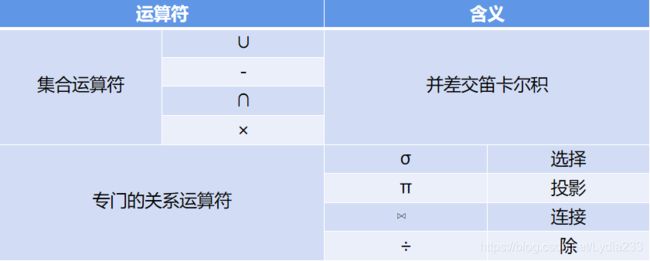
2.4.1传统的集合运算

1. 并
   关系R和S具有相同的目n（即两个关系都有n个属性），相应的属性取自同一个域。
   R与S的并运算表示为R∪S：R∪S={t|t∈RVt∈S}。
   运算结果为：n目关系，由属于R或属于S的元组组成。
2. 差
   关系R和S具有相同的目n（即两个关系都有n个属性），相应的属性取自同一个域。
   R与S的差运算表示为R-S：R-S={t|t∈R∧t∉S}。
   运算的结果为：n目关系，由属于R而不属于S的所有元组组成。
3. 交
   关系R和S具有相同的目n（即两个关系都有n个属性），相应的属性取自同一个域。
   R与S的交运算表示为R∩S：R∩S={t|t∈R∧t∈S}，R∩S=R-（R-S）。
   运算结果为：n目关系，由既属于R又属于S的元组组成。
4. 笛卡尔积
   严格地讲应该是广义的笛卡尔积。
   R：n目关系，$k_1$个元组，S：m目关系，$k_2$个元组
   R与S的笛卡尔积运算表示为R×S：
   $$R\times X=\{t_r{t}_s|t_r\in R\wedge t_s\in S\}$$

运算结果为：行：$k_1$×$k_2$个元组，列：（n+m）列元组的集合，其中元组的前n列是关系R的一个元组，后m列是关系S的一个元组。

2.4.2专门的关系运算

关系运算包括：选择、投影、连接、除运算。
相关记号说明：

• 关系模式为R（$A_1$，$A_2$，…，$A_n$），它的一个关系为R，t∈R表示t是R的一个元组。t[Ai]则表示元组t中相应于属性Ai的一个分量。
• 若A={$A_{i1}$，$A_{i2}$，…，$A_{ik}$}，其中$A_{i1}$，$A_{i2}$，…，$A_{ik}$是$A_1$，$A_2$，…，$A_n$中的一部分，则A称为属性列或属性组。
  t[A]=（t[$A_{i1}$,]，t[$A_{i2}$]，…，t[$A_{ik}$]）表示元组t在属性列A上诸分量的集合。¬A 则表示{$A_1$，$A_2$，…，$A_n$}中去掉{$A_{i1}$，$A_{i2}$，…，$A_{ik}$}后剩余的属性组。
• R为n目关系，S为m目关系，$T_r$∈R，$T_s$∈S，$T_r$ ⌒$T_s$ 称为元组的连接。$T_r$⌒$T_s$ 是一个n+m列的元组，前n个分量为R中的一个n元组，后m个分量为S中的一个m元组。
• 给定一个关系R（X，Z），X和Z为属性组。当t[X]=x时，x在R中的象集$Z_x$={t[Z]|t∈R，t[X]=x}，它表示R中属性组X上值为x的诸元组在Z上分量的集合。

1. 选择
   选择又称为限制。在关系R中选择满足给定条件的诸元组，记作：
   $${\sigma }_F(R)=\{t|t\in R\wedge F(t){=}^{\prime }{真}^{\prime }\}$$
   其中：F为选择条件，基本形式为：
   $$X_1\theta Y_1$$
   其中 θ表示比较运算符，它可以是＞，≥，＜，≤， ＝或＜＞。X1，Y1等是属性名，或为常量，或为简单函数；属性名也可以用它的序号来代替。
   条件表达式中的运算符如下表：
   
2. 投影
   从R中选择出若干属性列组成新的关系。
   $${\pi }_A(R)=\{t[A]|t\in R\}$$
   其中：A：R中的属性列。投影操作主要是从列的角度进行运算，投影之后不仅取消了原关系中的某些列，而且还可能取消某些元组（避免重复行）。
3. 连接
   又称为θ连接，表示从两个关系的笛卡尔积中选取属性间满足一定条件的元组。
   $$R\frac{\bowtie }{A\Theta B}S=\{t_r{t}_s|t_r\in R\wedge t_s\in S\wedge t_r[A]\theta t_s[B]\}$$
   A和B：分别为R和S上度数相等且可比的属性组。
   θ：比较运算符。
   运算结果：从R和S的广义笛卡尔积R×S中选取（R关系）在A属性组上的值与（S关系）在B属性组上满足比较关系θ的元组。
   两类常用连接运算：

• 等值连接
  θ为“=”的连接运算称为等值连接。
  等值连接的含义：从关系R与S的广义笛卡尔积中选取A、B属性值相等的那些元组。
  $$R\frac{\bowtie }{A=B}S=\{t_r{t}_s|t_r\in R\wedge t_s\in S\wedge t_r[A]=t_s[B]\}$$
• 自然连接
  自然连接是一种特殊的等值连接，两个关系中进行比较的分量必须是相同属性组，在结果中把重复的属性列去掉。
  自然连接的含义：R和S具有相同的属性组B。
  $$R\bowtie S=\{t_r{t}_s|t_r\in R\wedge t_s\in S\wedge t_r[B]=t_s[B]\}$$
  注意： 自然连接还需要取消重复列，所以是同时从行和列的角度进行运算。
• 悬浮元组：两个关系R和S在自然连接时，关系R和S中被舍弃的元组称为悬浮元组。
• 外连接：如果把悬浮元组舍弃的元组也保存在结果关系中，而在其他属性上填空值（Null），这种连接就叫做外连接。
• 左外连接：如果只保留左边关系R中的悬浮元组叫做左外连接。
• 右外连接：如果只保留右边关系S中的悬浮元组叫做右外连接。

4. 除
   给定关系R（X，Y）和S（Y，Z），其中X，Y，Z为属性组。R中的Y与S中的Y可以有不同的属性名，但必须出自相同的域集。
   R与S的除运算得到一个新的关系P（X），P是R中满足下列条件的元组在X属性列上的投影：
   元组在X上分量值x的象集Yx包含S在Y上投影的集合，记作：
   $$R÷S=\{tr[X]|tr\in R\wedge \pi Y(S)\subseteq Yx\}$$
   Yx：x在R中的象集，x=tr[X]
   注意：除操作是同时从行和列角度进行计算。

2.5*关系演算

关系演算是以数理逻辑中的谓词演算为基础的。按谓词变元的不同，关系演算可分为元组关系演算和域关系演算。

2.5.1元组关系演算语言ALPHA

元组关系演算以元组变量作为谓词变元的基本对象。一直典型的元组关系演算语言是ALPHA语言。
ALPHA语言主要有GET，PUT，UPDATE，DELETE，DROP6条语句。

语句的基本格式是：
操作语句 工作空间名（表达式）： 操作条件
表达式用于说明要查询的结果，它可以是关系名或（和）属性名。
操作条件是一个逻辑表达式，说明查询结果要满足的条件，用于将操作结果限定在满足条件的元组中，操作条件可以为空。
除此之外，还可以在基本格式的基础上加上排序要求、定额要求等。

1. 检索操作

检索操作用GET语句实现

• 简单检索（即不带条件的检索）
• 限定的检索（即带条件的检索）
• 带排序的检索
• 指定返回元组的个数
• 用元组变量的检索

元组变量是在某一关系范围内变化（所以也称范围变量），一个关系可以设置多个元组变量。元组变量主要有两方面的用途：
①简化关系名。如果关系的名字很长，使用起来就会感到不方便，这时可以设置一个较短的名字的元组变量来代替关系名。
②操作条件中使用量词时必须用元组变量。 ALPHA语言用RANGE来说明元组变量。

• 用存在量词的检索条件中使用量词时必须用元组变量
• 带有多个关系的表达式的检索
• 用全称量词的检索
• 用两种量词的检索
• 用蕴含的检索
• 聚集函数
  使用查询语言时，进行监督的计算。关系数据语言中建立了有关这类运算的标准函数库。这类函数通常称为聚集函数或内置函数。常用的聚集函数COUNT，TITAL，MAX，MIN，AVG等。

函数名	功能
COUNT	对元组计数
TOTAL	求总和
MAX	求最大值
MIN	求最小值
AVG	求平均值

2. 更新操作

• 修改操作
  修改操作用UPDATE语句实现。其步骤是：
  ①首先用HOLD语句将修改的元组从数据库中读到工作空间中；
  ②然后用宿主语言修改工作空间中元组的属性值；
  ③最后用UPDATE语句将修改后的元组送回数据库中。注意：单纯检索数据使用GET语句即可，但为修改数据而读元组时必须使用HOLD语句，HOLD语句是带上并发控制的GET语句。
  说明：
  ①如果修改操作涉及到两个关系的话，就要执行两次HOLD-MOVE-UPDATE操作系列。
  ②在ALPHA语言中，修改关系主码的操作是不允许的。
  ③如果需要修改主码值，只能先用删除操作删除该元组，然后再把具有新主码值的元组插入到关系中。
• 插入操作
  插入操作用PUT语句实现。其步骤是：
  ①首先用宿主语言在工作空间中建立新元组；
  ②然后用PUT语句把该元组存入指定的关系中。
  PUT语句只对一个关系操作，也就是说表达式必须为单个关系名。
• 删除
  删除操作用DELETE语句实现。其步骤为：
  ①用HOLD语句把要删除的元组从数据库中读到工作空间中；
  ②用DELETE语句删除该元组。

2.5.2元组关系演算

为了讨论方便，先允许关系（的基数）是无限的。然后再对这种情况下定义的演算作适当的修改，保证关系演算中的每一个公式表示的是有限关系。
在元组关系演算系统中，称{t|Φ（t）}为元组演算表达式。其中t是元组变量，Φ（t）为元组关系演算公式简称公式。它由原子公式和运算符组成。

原子公式有三类：

• R（t）
  R是关系名，t是元组变量。R（t）表示t是R中的元组。于是，关系R可表示为{t|R（t）}
• t[i]Θu[j]
  t和u是元组变量，Θ是算术比较运算符。t[i]Θu[j]表示断言“元组t的第i个分量与元组u的第j个分量满足比较关系Θ”。
• t[i]Θc或cΘu[i]
  这里c是常量，该公式表示“t的第i个分量与常量c满足比较关系Θ”。
  在关系演算中定义了“自由元组变量”和“约束元组变量”的概念。这些概念和谓词演算中的概念完全一样。若公式中的一个元组变量前有“全称量词”或“存在量词”，则称该变量为约束元组变量，否则称自由元组变量。
  公式可以递归定义如下：
• 如果原子公式是公式。
• 如果Φ1，和Φ2是公式，则Φ1∧Φ2，Φ1∨Φ2，┐Φ1也是公式。分别表示为：
  如果Φ1和Φ2同时为真，则Φ1∧Φ2才为真，否则为假；
  如果Φ1和Φ2中一个或同时为真，则Φ1∨Φ2为真，仅当Φ1和Φ2同时为假时，Φ1∨Φ2才为假；
  若Φ1为真，则┐Φ1为假。
• 若Φ是公式，则∃t（Φ）也是公式。其中符号∃是存在量词符号，∃t（Φ）表示：若有一个t使Φ为真，则∃t（Φ）为真，否则∃t（Φ）为假。
• 若Φ是公式，则∀t（Φ）也是公式。其中符号∀是全称量词符号，∀t（Φ）表示：如果对所有t，都使Φ为真，则∀t（Φ）为真，否则∀t（Φ）为假。
• 在元组演算公式中，各种运算符的优先次序为：
  ①算术比较运算符最高；
  ②量词次之，且∃的优先级高于∀的优先级；
  ③逻辑运算符最低，且┐的优先级高于∧的优先级，∧的优先级高于∨的优先级；
  ④加括号时，括号中运算符优先，同一括号内的运算符之优先级遵循①，②，③各项。
• 有限次地使用上述五条规则得到的公式是元组关系演算公式，其他公式不是元组关系演算公式。
  一个元组演算表达式{t|Φ（t）}表示了使Φ（t）为真的元组集合。
  关系代数的运算均可以用关系演算表达式来表示（反之亦然）。
  下面用关系演算表达式来表示五种基本运算：
  1）并，R∪S={t|R（t）∨S（t）}
  2）差，R-S={t|R（t）∧┐S（t）}
  3)笛卡尔积：
  $$R\times S=\{t^{(n+m)}|(\exists u^{(n)})(\exists v^{(m)})(R(u)\wedge S(v)\wedge t[1]=u[1]\wedge ...\wedge t[n]=u[n]\wedge t[n+1]=v[1]\wedge ...\wedge t[n+m]=v[m])\}$$
  这里$t^{(m+n)}$表示t的数目是(n+m）。

4）投影
$$\prod _{i_1,i_2,L,i_k}(R)=\{t^{(k)}|(\exists u)(R(u)\wedge t[1]=u[i_1]\wedge L\wedge t[k]=u[i_k])\}$$
5）选择
$${\sigma }_F(R)=\{t|R(t)\wedge F^{\prime }\}$$
$F^{\prime }$是公式F用t[i]代替运算对象i得到的等价公式。

安全限制：把不产生无限关系的表达式称为安全表达式，所采取的措施称为安全限制。
安全限制通常是定义一个有限的符号集dom（Φ），dom（Φ）一定包括出现在Φ以及中间结果和最后结果的关系中的所有符号（实际上是各列中值的汇集），dom（Φ）不必是最小集。
当满足下列条件时，元组演算表达式{t|Φ（t）}是安全的：
1）如果t使Φ（t）为真，则t的每个分量是dom（Φ）中的元素。
2）对于Φ中的每一个形如（∃u）（W（u））的子表达式，若u使W（u）为真，则u的每个分量是dom（Φ）中的元素。
3）对于Φ中的每一个形如（∀u）（W（u））的子表达式，若u使W（u）为假，则u的每个分量必属于dom（Φ）。换言之，若u某一分量不属于dom（Φ），则W（u）为真。

2.5.3域关系演算语言QBE

关系演算的另一种形式是域关系演算。域关系演算以元组变量的分量即域变量作为谓词变元的基本对象。
QBE是Query By Example（即通过例子进行查询）的简称，它是基于屏幕表格的查询语言，用户通过终端屏幕编辑程序以填写表格的方式构造查询要求，而查询结果也是以表格形式显示。QBE中用示例元素来表示查询结果可能的情况，示例元素实质上就是域变量。
QBE操作框架

1. 检索操作
   1）简单查询
   2）条件查询
   3）聚集函数

函数名	功能
CNT	对元组计数
SUM	求总和
AVG	求平均值
MAX	求最大值
MIN	求最小值

4）对查询结果排序
对查询结果按某个属性值的升序排序，只需在相应列中填入“AO.”，按降序排序则均“DO.”。如果按多列排序，用“AO（i）.”或“DO（i）.”表示，其中i为排序的优先级，i值越小，优先级越高。
2. 更新操作
1）修改操作
修改操作符为“U.”。
在QBE中，关系的主码不允许修改，如果需要修改缪戈元组的主码，只能先删除该元组，然后再插入新的主码的元组。
2）插入操作
插入操作符为“I.：。新插入的元组必须具有码值，其他属性值可以为空。
3）删除操作
删除操作符为“D.”。