Numpy实现神经网络-手写数字识别

 使用numpy实现神经网络的前向传播，以及反向传播，使用矩阵计算加快运算速度，理论推导则在以前的博客中。

多层感知机梯度推导

import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
from tensorflow.keras import datasets

batch_size = 256
epochs = 200
lr = 0.01

(x_train, y_train), (x_test, y_test) = datasets.mnist.load_data()
y_train = tf.one_hot(y_train, depth=10)
y_test = tf.reshape(y_test, [y_test.shape[0], 1])

x_train = tf.reshape(x_train, [-1, 28*28])
x_test = tf.reshape(x_test, [-1, 28*28])

train_data = tf.data.Dataset.from_tensor_slices((x_train, y_train))
train_data = train_data.shuffle(10000).batch(batch_size, drop_remainder=True)

test_data = tf.data.Dataset.from_tensor_slices((x_test, y_test))
test_data = test_data.batch(batch_size, drop_remainder=True)

这里首先引入数据集，使用tf2.0 的datasets中的mnist，然后将数据集使用Dataset进行打包，分割。详细api可以参见tf2.0官方文档。这里稍微注意一下如果使用Dataset预处理数据集，会返回一个tensor，使用时需要将tensor转换为numpy。

def sigmoid(z):
    return 1.0 / (1.0 + np.exp(-z))


class MLP:
    # 输入数据[b, width, height] => [b, 784]
    # 前向传播
    # 反向传播
    # sgd更新权重
    def __init__(self, sizes, batch):
        """

        :param sizes: [784, 30, 10]
        """
        self.sizes = sizes
        self.num_layers = len(sizes) - 1
        # w [784, 30], [30, 10], [ch_input, ch_out]
        # b [ 30, 10]
        self.weights = [np.random.randn(ch1, ch2) for ch1, ch2 in zip(sizes[:-1], sizes[1:])]
        self.bias = [np.random.randn(bias) for bias in sizes[1:]]

    def forward_predict(self, x):
        """

        :param x: [b, 784]
        :return:[b, 10]
        """
        for w, b in zip(self.weights, self.bias):
            logit = np.dot(x, w) + b
            x = sigmoid(logit)

        return x

    def backward(self, x, y):
        """

        :param x: [b, 784]
        :param y: [b, 10] one-hot
        """
        nabla_w = [np.zeros(w.shape) for w in self.weights]
        nabla_b = [np.zeros(b.shape) for b in self.bias]

        # 保存每一层的输出
        activations = [x]

        activation = x

        for b, w in zip(self.bias, self.weights):

            z = np.dot(activation, w) + b
            activation = sigmoid(z)
            activations.append(activation)


        loss = np.sum(np.power((activations[-1] - y), 2))
        # backward
        # 计算每层梯度
        # 1. 计算输出层梯度
        # sigmoid([b, 10]) , [b, 10]
        delta = activations[-1] * (1 - activations[-1]) * (activations[-1] - y)

        # [b, 10]
        nabla_b[-1] = delta

        # [30, 10] = [30, b] @ [b, 10]
        nabla_w[-1] = np.dot(activations[-2].T, delta)

        # 从倒数第二层开始
        for l in range(2, self.num_layers + 1):
            l = -l
            a = activations[l]
            # [b, 30]
            # weights [784, 30], [30, 10]
            delta = np.dot(delta, self.weights[l+1].T) * a * (1 - a)
            nabla_b[l] = delta
            nabla_w[l] = np.dot(activations[l-1].T, delta)

        return nabla_w, nabla_b, loss

    def train(self, train_data, epochs, lr, test_data):
        """

        :param train_data: ([batch_size, 784], [b, 10])
        :param epochs: 100
        :param lr: 0.01
        :param test_data: ([batch_size, 784], [b, 10])

        """
        losses = []

        for epoch in range(epochs):
            loss = 0
            train_total, train_correct = 0, 0
            for step, (x, y) in enumerate(train_data):
                x = x.numpy()
                y = y.numpy()
                loss += self.update_mini_batch(x, y, lr)
                train_correct += self.evaluate(x, y)
                train_total += y.shape[0]

            losses.append(loss)
            print('train_epcho, loss, acc', epoch, loss, train_correct / train_total)
            if test_data is not None:
                total, correct = 0, 0
                for _, (x_test, y_test) in enumerate(test_data):
                    correct += self.evaluate(x_test, y_test)
                    total += y_test.shape[0]
                print("Epoch, accuracy:", epoch,  correct / total)
        return losses

    def update_mini_batch(self, x, y, lr):
        """

        :param x: [b, 784]
        :param y: [b, 10]
        """

        # [784, 30], [30, 10]
        nabla_w = [np.zeros(w.shape) for w in self.weights]
        nabla_b = [np.zeros(b.shape) for b in self.bias]
        batch = x.shape[0]
        losses = 0
        for i in range(batch):
            one_x = x[i, :]
            one_y = y[i, :]
            one_x = np.reshape(one_x, (1, len(one_x)))
            one_y = np.reshape(one_y, (1, len(one_y)))

            nabla_w_, nabla_b_, loss = self.backward(one_x, one_y)

            nabla_w = [acc+cur for acc, cur in zip(nabla_w, nabla_w_)]
            nabla_b = [acc+cur for acc, cur in zip(nabla_b, nabla_b_)]

            loss = loss / batch
            losses += loss
        nabla_w = [w/batch for w in nabla_w]
        nabla_b = [b/batch for b in nabla_b]

        # w = w - lr * nabla_w
        self.weights = [w - lr * nabla for w, nabla in zip(self.weights, nabla_w)]
        self.bias = [b - lr * nabla for b, nabla in zip(self.bias, nabla_b)]

        return losses

    def evaluate(self, x_test, y_test):
        """

        :param x_test: [b, 784]
        :param y_test: [b, 10]
        """
        result = self.forward_predict(x_test)
        predic_idx = np.argmax(result, axis=1)
        true_idx = np.argmax(y_test, axis=1)

        correct = np.sum(predic_idx == true_idx)

        return correct

这里激活函数使用的sigmoid函数，同时使用一个列表保存结点信息。在反向传播中，需要首先计算输出层的delta, 通过最后一层的delta不断递推后一层的delta就可以得到相应的梯度了，详细证明在我以前的博客中。

def main():
    sizes = [784, 30, 10]
    mlp = MLP(sizes, batch_size)

    losses = mlp.train(train_data, epochs=epochs, lr=lr, test_data=test_data)

    epoch = [i for i in range(epochs)]

    plt.plot(epoch, losses)
    plt.show()


if __name__ == '__main__':
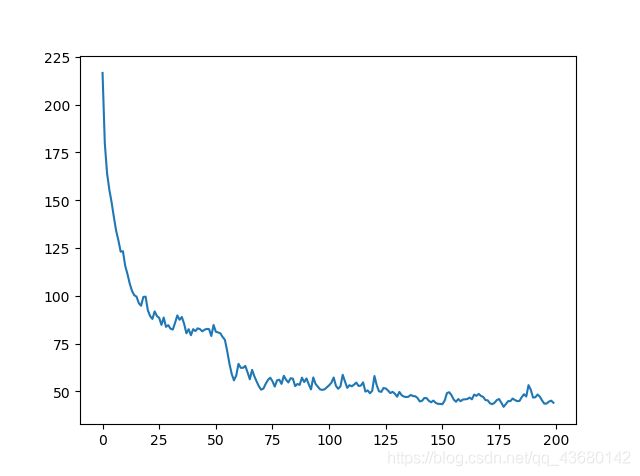
    main()

最后就是测试效果了，loss 如下：