Transformer模型深入理解
论文: Attention is All You Need
1 模型总览
整个模型的结构是标准的Encoder-Decoder结构, Encoder部分堆叠6个相同的encoder层, Decoder部分同样堆叠6个相同的decoder层。
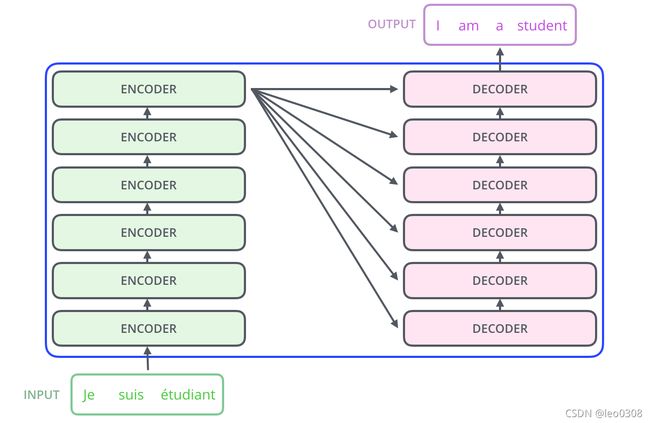
继续深入模型的内部, 每个encoder层包含2部分: 一个自注意力层和一个前馈层。
每个decoer层包含3部分: 一个自注意力层, 一个交叉注意力层和一个前馈层。

再继续深入,网络还采用了残差结构, 每个自注意力层和前馈层之后都进行了残差连接, 并且使用了归一化。
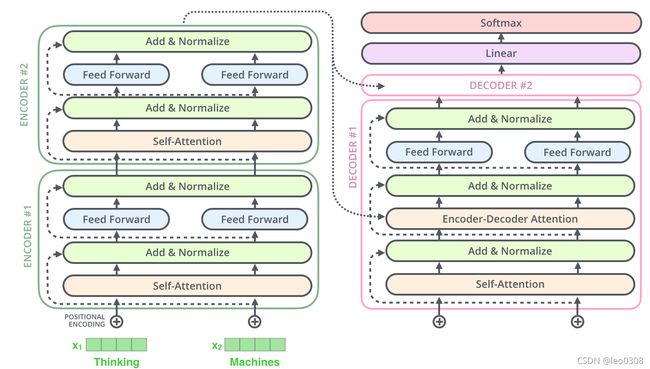
2 Attention机制理解
2.1 注意力详细解释
整个模型中最核心的部分就是Attention的运用了, 其实Attention机制并不是Transformer这篇文章提出来的, 而是早已有之, 只是Transformer这篇文章是首次纯使用Attention,并且结果十分惊艳, 让Attention机制深入人心。
先抛开公式和数学解释不谈, 通俗易懂地理解Attention机制就是根据加权系数对信息进行加权融合。那最重要的问题就是找到合适的加权系数了,这里还是抛开数学, 举一个形象化的例子说明: 假设有一个翻译任务, 把中文的我爱你翻译成英文的I love you,那么我们在翻译‘我’这个字的时候是否就仅仅关注这一个字呢, 显然多关注一些其他的字也是有帮助的,那么我们在编码’我’这个字的时候除了关注‘我’这个字本身以外,还可以关注‘爱’和‘你’这2个字, 我们可以给他们分别赋上一个重要性的系数, 比如[0.8,0.1,0.1], 那么’我’这个字的编码信息里面就融合了0.8的‘我’, 0.1的‘爱’和‘0.1’的你。 这个例子非常简单, 但形象地说明了Attention机制的作用, 对理解很有帮助。
上面例子中的加权系数是我随手编的, 实际中是怎么得到的呢? 这就要结合数学公式来理解了。 其实公式也非常简单, 知道它的作用后就很好理解了。
A t t e n t i o n ( Q , K , V ) = s o f t m a x ( Q K T d k ) V Attention(Q, K, V)=softmax(\frac{QK^T}{\sqrt{d^k}})V Attention(Q,K,V)=softmax(dkQKT)V
这是文章中的公式, Q, K, V都是大写的, 是一个矩阵, 其实这个公式不方便Attention机制的理解, 只是实际运算中为了效率把这个操作矩阵化了而已。 为了方便理解, 我们一个一个看,
A t t e n t i o n ( q , k , v ) = s o f t m a x ( q k T d k ) v Attention(q, k, v)=softmax(\frac{qk^T}{\sqrt{d^k}})v Attention(q,k,v)=softmax(dkqkT)v
两个公式是一样的, 只不过上面矩阵化的版本是同时并行处理多个。
q, k, v分别代表查询向量, 键向量和值向量。 这些概念都是从信息检索领域来的, 有非常明确的数学含义, 我们先不用深究,反正知道它背后有明确的理论支撑就可以了。
Transformer中有2种注意力机制: 自注意力和交叉注意力。所谓自注意力, 就是q, k和v都是从同一个输入得到的。
我们还是举个例子来解释这个公式的原理:
假设还是翻译中文‘我爱你’, 这3个字每个都用1024维向量表示,我们先看‘我’这个字, 它是一个1x1024维的向量, 记为x1, 我们把x1投影到一个更低的维度(不一定需要更低, 只是通常的选择), 比如128, 我们得到一个1x128的向量,把这个过程重复3次, 我们就得到3个投影向量, 作为 q1,k1,v1。这里用同一个x1得到的q1 ,k1,v1向量, 所以叫自注意力。 q 1 k 1 T q_{1}k_{1}^T q1k1T运算得到的是一个实数值 w 11 w_{11} w11,这个过程其实就是一个求相似度的过程, 得到的实数值 w 11 w_{11} w11就衡量了2个向量之间的相似度。这就是编码’我’这个字的时候赋予‘我’这个字的加权系数, 同样地我们可以得到‘爱’这个字的向量表示x2, 以及q2, k2, v2 3个向量, q 1 k 2 T q_{1}k_{2}^T q1k2T运算得到的是一个实数值 w 12 w_{12} w12,这就是编码’我’这个字的时候赋予‘爱’这个字的加权系数。 同样地, 我们可以得到 w 13 w_{13} w13,也就是编码’我’这个字的时候赋予‘你’这个字的加权系数 。假设编码后的‘我’用z1表示:
z 1 = w 11 x 1 + w 12 x 2 + w 13 x 3 z_1= w_{11}x_1+w_{12}x_2+w_{13}x_3 z1=w11x1+w12x2+w13x3
上述公式的含义就是编码‘我’这个字的时候融合了 w 11 w_{11} w11的‘我’, w 12 w_{12} w12的‘爱’, w 13 w_{13} w13的‘你’。 这就是我一开始提到的Attention机制就是根据加权系数对信息进行加权融合。
上述过程是对‘我’的编码,对‘爱’和‘你’的编码是完全相同的过程。
z 2 = w 21 x 1 + w 22 x 2 + w 23 x 3 z_2= w_{21}x_1+w_{22}x_2+w_{23}x_3 z2=w21x1+w22x2+w23x3
z 3 = w 31 x 1 + w 32 x 2 + w 33 x 3 z_3= w_{31}x_1+w_{32}x_2+w_{33}x_3 z3=w31x1+w32x2+w33x3
把上述的过程用矩阵表达就是:
{ z 1 z 2 z 3 } = { w 11 w 12 w 13 w 21 w 22 w 23 w 31 w 32 w 33 } ∗ { x 1 x 2 x 3 } \left\{ \begin{matrix} z_1 \\ z_2 \\ z_3 \\ \end{matrix} \right\} = \left\{ \begin{matrix} w_{11} & w_{12} & w_{13} \\ w_{21} & w_{22} & w_{23} \\ w_{31} & w_{32} & w_{33} \\ \end{matrix} \right\} * \left\{ \begin{matrix} x_1 \\ x_2 \\ x_3 \\ \end{matrix} \right\} ⎩⎨⎧z1z2z3⎭⎬⎫=⎩⎨⎧w11w21w31w12w22w32w13w23w33⎭⎬⎫∗⎩⎨⎧x1x2x3⎭⎬⎫
这也是一开始用矩阵表示的公式的由来。
注意公式中还有2点没讲到, 一个是分母除了一个值 d k \sqrt{d_k} dk,这个是为了防止Q和K相乘后数值变大导致溢出, 尽量保证数值的稳定性; 另一个就是Q和K相乘后有一个取softmax的操作, 这点也很好理解, softmax可以把数值进行归一, 同时和为1 ,就比较像概率了。
2.2 多头注意力机制
实践中一般都是采用多头注意力机制,比如Transformer中采用了8个注意力头。 多头注意力机制就是并行有多个注意力层, 把所有的注意力层结果拼接起来。直观理解就是不同的注意力头是一个不同的子空间, 可以在不同的维度上进行信息编码。 举个例子 ,还是翻译’我爱你’, 假设现在有2个注意力头,
z 1 = 0.8 x 1 + 0.1 x 2 + 0.1 x 3 z_1= 0.8x_1+0.1x_2+0.1x_3 z1=0.8x1+0.1x2+0.1x3
z 1 ′ = 0.4 x 1 + 0.4 x 2 + 0.2 x 3 z_1'=0.4x_1+0.4x_2+0.2x_3 z1′=0.4x1+0.4x2+0.2x3
可以看到两个注意力头分别有不同的关注点, 第一个注意头编码‘我’的时候主要注意‘我’这个字, 第二个注意力头给‘我’和‘爱’都较高的关注。 这增加了信息表征的多样性。
用公式表示上面的描述就是:
M u t i H e a d ( Q , K , V ) = C o n c a t ( h e a d 1 , h e a d 2 , . . . h e a d n ) W o MutiHead(Q, K, V)= Concat(head_1,head_2,...head_n)W^o MutiHead(Q,K,V)=Concat(head1,head2,...headn)Wo
其实融合的方式可以是其他的, 这里选择了concat操作, 并且在concat之后在乘上一个系数。 这些不是必须的, 只是实践中的选择。
采用多头注意力相比单头注意力运算量是差不多的, 这是因为采用多头时我们会减少qkv这3个向量的维度, 比如采用单头时, qkv的维度是512, 当我们采用8个注意力头时, 我们把qkv的维度变为64。这样计算量是相同的, 只是最后concat之后额外乘了一个矩阵增加了一些计算量。
3 其他模块
3.1 Embding
Embedding比较简单,就是一个词嵌入表示, 假设词表总共有30000个词, 每个词都用1024维向量表示, 那么就是一个30000x1024维的查找表,根据索引可以得到每个词的向量表示。Transformer中的Embedding是可以学习的,直接用了nn.Embedding(), 本质上就是一个查找表,Transformer中对这一部分也是学习的。 其实应该也可以用已经训练好的词表,比如提前用word2vec训练好了一个词表, 或者在网上下了一个别人训好的词表。
3.2 位置编码
之所以有位置编码是因为Attention的结构丢失了位置信息, 换句话说不同顺序的语句经过Attention后都是一样的, 这显然是不合理的, 因为语句的顺序是很重要的。 位置编码方式有很多种,比如常见的有相对位置编码和绝对位置编码, 这些都是不需要学习的, 也有把位置参数也作为变量进行学习的做法。 对位置编码进行改进也是Transformer中一个热门的研究方向。 原始的Transformer中采用了相对位置编码的方式 。
比如一个词用1024维向量表示 , 位置编码也是1024维向量, Transformer中直接把词嵌入表示和位置编码进行相加操作进行融合。
3.3 mask机制
3.4 输出表示
模型的输出是怎么得到具体的单词的呢? 比如翻译’我‘, 模型最后的输出的是一个向量, 如何根据这个向量得到表示的单词呢,比如翻译正确的话我们要得到‘I’。这就涉及到反向的映射,前面讲Embedding的时候我们讲到了正向的映射, 即把单词转换为向量表示。 现在需要把向量转换回实际的单词。 这个过程也非常简单, 首先我们也有一个输出的词表(对翻译来说, 一般是不同的词表, 比如输入是中文词表, 输出是英文词表, 对其他任务来说, 输入输出有时可以用同一个词表),然后模型会输出一个向量, 向量经过一个fc层得到维度和词表大小相同的新向量, 再经过一个softmax层得到概率, 取概率最大的那个索引, 用这个索引去输出词表进行查询, 就得到输出的单词了。 图示如下:

4 参考
1 The Illustrated Transformer 这是一篇非常优秀的解读Transformer的博客, 用图解的方式解析了transformer的原理以及过程, 另外这个博客上中还附上了各种翻译版本。顺便说一句, 这个博客的作者和Transformer文章的作者都是同一个团队的, 因此这篇博客也算是官方解读了。
2 Visualizing A Neural Machine Translation Model (Mechanics of Seq2seq Models With Attention 这篇博客和上面的是同一个作者, 可视化地讲解了seq2seq 模型。
网络上的大多数博客都是这2篇博客翻译过来的。建议直接看原文, 更有助于理解。
3 The Annotated Transformer 这是哈佛大学NLP团队对Transformer写的一个指导, 并用pytorch进行了代码实现。