财经数据分析/金融量化投资-机器学习预测沪深300走势
机器学习预测沪深300指数走势
摘 要
沪深300指数作为中国股票价格指数的代表,也是中国股指期货的标的指数,对其走势预测具有积极的现实意义与应用价值。本文通过计算交易特征指标和涨跌决策变量,其中涨用+1表示,否则为-1,最终把问题转化为分类问题,并利用支持向量机、神经网络和逻辑回归进行涨跌趋势预测。这里介绍了如何将实际问题转化为分类问题,并利用分类模型进行预测,这种技能在实际数据挖掘中尤为重要。
关键词: 机器学习;沪深300;支持向量机;神经网络;逻辑回归
Prediction of Shanghai and Shenzhen 300 Index by Machine Learning
Abstract
As the representative of China's stock price index and the target index of China's stock index futures, Shanghai and Shenzhen 300 Index has positive practical significance and application value for its trend prediction. In this paper, by calculating the trading characteristic index and the fluctuation decision variables, where the fluctuation is represented by +1, otherwise it is -1, the problem is finally transformed into a classification problem, and the fluctuation trend is predicted by using support vector machine, neural network and logistic regression. This paper introduces how to transform practical problems into classification problems and use classification models to make predictions. This skill is especially important in practical data mining.
Keywords:Machine learning; Shanghai and Shenzhen 300; Support vector machine; Neural network; Logistic regression
目 录
一、绪论...................................................... 1
(一)研究背景 1
(二)研究目的和意义 1
(三)设计思路 1
二、系统分析.................................................. 1
(一)需求分析 1
(二)可行性分析 2
1.经济可行性 2
2.技术可行性 2
3.法律可行性 2
4.运行可行性 2
三、基于机器学习的量化投资策略代码的具体实现.................. 2
(一)开发工具的简介 2
(二)下载数据 3
(三)数据处理 4
(四)计算决策变量Y和上涨下跌的天数 6
(五)划分训练集和测试集 6
(六)支持向量机 6
1.原理 6
2.代码 6
(七)逻辑回归 7
1.原理 7
2.代码 8
(八)神经网络 8
1.原理 8
2.代码 9
(九)数据可视化 10
1. 收益率可视化 10
2. 预测涨跌天数柱状图 10
3. 预测涨跌天数折线图 10
四、系统测试与运行结果....................................... 11
(一)系统测试方法 11
(二)本系统测试结果 11
五、结 论.................................................... 13
参考文献..................................................... 13
六、源代码..................................................... 13
一、绪论
(一)研究背景
大数据和另类数据,AI人大数据和另类数据,工智能和云计算等新工具已成为金融业的主要发展趋势。早在2019英格兰银行和英国金融行为监管局做的一项调查就发现,三分之二的英国金融公司已经在使用机器学习(Machine Learning,ML),被调查的公司认为他们使用机器学习的领域数量在未来三年内将增加一倍以上。ML机器学习是AI人工智能的一部分,属于计算科学领域,专门分析和解释数据的模式及结构,以实现无需人工交互即可完成学习、推理和决策等行为的目的。对于量化基金经理来说,ML机器学习拓展了他们的工具包里可用的工具。
和普通的股票分析不同,机器学习不是简单粗暴地给出一个假设,而是通过基于大数据的深度学习来推断出可预测目标和成因的相关性。随着人工智能及大数据在各行各业的运用愈发深入,机器学习也开始被应用于投资的各个不同领域。
(二)研究目的和意义
将各种数学理论、数据挖掘技术应用到股票分析软件中,并且通过对历史交易数据的研究,从而得到股票的在走势规律。通过机器学习的方式,可以在运用过程中依据数据的不断学习优化,完善预测模型,来达到成功预测股票涨幅,进而达到盈利的目的。
(三)设计思路
将实际问题转化为分类问题,并利用分类模型进行预测。通过计算交易特征指标和涨跌决策变量,其中涨用+1表示,否则为-1,最终把问题转化为分类问题,并利用支持向量机、神经网络和逻辑回归进行涨跌趋势预测。
对于该系统的设计主要满足以下方面:
- 界面整洁,操作简便。
- 功能齐全,包括支持向量机、神经网络和逻辑回归进行涨跌趋势预测。
- 各个功能模块之间相互独立,使得系统能够进行扩展,且便于维护。
- 功能符合实际需要。所有分析数据均来源于国泰安CSMAR数据库。
- 前后台代码分离,便于保护数据。
- 系统可以稳定的运行。
二、系统分析
(一)需求分析
自股票诞生之日起,人们对股票预测的研究便从未停歇,准确预测股票走势可以为投资者带来丰厚的投资回报,同时规避投资风险。股票市场是一个复杂非线性系统,传统时间序列建模分析方式存在很大的局限性,机器学习方法在处理非线性问题时具有较强能力。机器学习目前广泛应用于股票预测及其相关研究,与传统股票建模预测分析方法相比,基于机器学习的股票预测分析方法具有较好的预测效果。
(二)可行性分析
1.经济可行性
软件开发中的经济可行性粗略来讲是指在开发软件之前,估算该软件为企业带来的收益在抵消开发和设计该软件所耗费的经济资源后是否还有剩余,及该软件是否能为企业带来净收益,所获得的净收益的多少是否值得企业开发该软件。而本软件设计和开发所需人员和资源极少,且开发出软件后能够极大增加股票的收益,所以在经济上认为该软件是可行的。
2.技术可行性
技术可行性通常是说在现有技术下软件能否顺利运行,设计出的软件是否具有现实中的可操作性。
运行本程序的软件方面,本程序使用spyder作为开发工具来进行软件的设计,并且使用国泰安作为数据来源,这两个软件都是非常成熟的开发软件,所以本系统在安全性、可运行性等方面是可行的。
运行本系统的硬件方面,由于现在电脑都已达到4G内存,硬盘也基本都在500G以上,在网页上流畅运行本系统基本上没有压力,所以说本系统在硬件上来说是完全可行的。
3.法律可行性
本系统所有的资料以及技术都是合理合法的,不存在任何违反规定并侵害他人权益的现象存在,且开发的过程中没有涉及任何的法律责任。因此本系统在法律上是可行的。
4.运行可行性
本程序操作简单,且软件运行的成本非常低,所需资源少,故本程序具有运行可行性。
综上所述,本系统是可行的。
三、基于机器学习的量化投资策略代码的具体实现
(一)开发工具的简介
Spyder是Python(x,y)的作者为它开发的一个简单的集成开发环境。和其他的Python开发环境相比,它最大的优点就是模仿MATLAB的“工作空间”的功能,可以很方便地观察和修改数组的值。
Spyder的界面由许多窗格构成,用户可以根据自己的喜好调整它们的位置和大小。当多个窗格出现在一个区域时,将使用标签页的形式显示。例如在图1中,可以看到“编辑”、“变量浏览器”、“文件”、“控制台”、“历史”以及两个显示图像的窗格。在查看菜单中可以设置是否显示这些窗格。
Spyder的功能比较多,比如:
- 在控制台中,可以按Tab按键进行自动补全。在变量名之后输入“?”,可以在“Object inspector”窗格中查看对象的说明文档。此窗格的Options菜单中的“Show source”选项可以开启显示函数的源程序。
- 可以通过“Working directory”工具栏修改工作路径,用户程序运行时,将以此工作路径作为当前路径。例如我们只需要修改工作路径,就可以用同一个程序处理不同文件夹下的数据文件。
- 在程序编辑窗口中按住Ctrl键,并单击变量名、函数名、类名或模块名,可以快速跳转到定义位置。如果是在别的程序文件中定义的,将打开此文件。在学习一个新模块的用法时,我们经常需要查看模块中的某个函数或类是如何实现的,使用此功能可以帮助我们快速查看和分析各个模块的源程序。例如下面的程序从不同的扩展库载入了一些模块和类。用Spyder打开此文件,按住Ctrl键,并单击signal、pl、HasTraits、Instance、View、Item、lfilter、plot、title等,将打开定义它们的程序文件,并跳转到相应的行。
CSMAR数据库(China Stock Market & Accounting Research Database)是深圳希施玛数据科技有限公司从学术研究需求出发,借鉴CRSP、COMPUSTAT、TAQ、THOMSON等权威数据库专业标准,并结合中国实际国情开发的经济金融领域的研究型精准数据库。 经过21年的不断积累和完善,CSMAR 数据库已涵盖因子研究、人物特征、绿色经济、股票、公司、海外、资讯、基金、债券、行业、经济、商品期货等18大系列,包含160+个数据库、4000多张表、5万多个字段。【单表查询】模块可以针对CSMAR 数据库的4000+张表进行时间、代码、指标设置,获取特定研究数据,可以导出Excel、CSV、TXT等多种资料格式。
(二)下载数据
下载2019年6月1日至2022年6月1日的沪深300的数据(最多只能下载四年数据),包括交易所指数代码,交易日期,开盘指数,最高指数,最低指数,收盘指数,成分证券成交量,成分证券成交金额,指数回报率等。所有分析数据均来源于国泰安CSMAR数据库。
字段依次表示指数代码、交易日期、开盘价、最高价、最低价、收盘价、成交量。请计算如下指标:
| A1(收盘价 / 均价) |
收盘价 / 过去 10 个交易日的移动平均收盘价 |
| A2(现量 / 均量) |
成交量 / 过去 10 个交易日的移动平均成交量 |
| 即A3(收益率) |
( 当日收盘价 - 前日收盘价 )/ 前日收盘价 |
| A4(最高价 / 均价) |
最高价 / 过去 10 个交易日的移动均平均收盘价 |
| A5(最低价 / 均价) |
最低价 / 过去 10 个交易日的移动平均收盘价 |
| A6(极差) |
最高价 - 最低价(衡量波动性) |
| A7(瞬时收益) |
收盘价 - 开盘价 |
Y(决策变量):后交易日收盘价 - 当前交易日收盘价,如果大于 0,记为 1;如果小于等于 0,记为 -1。
同时对指标A1~A7作标准化处理:( 当前值 - 均值 )/ 标准差
(三)数据处理
- 读取数据
td=pd.read_excel('hs3002.xlsx')- 查看前6行
td.head(6)- A1收盘价除以过去10日移动平均收盘价
A1=td['Idxtrd05'].values/td['Idxtrd05'].rolling(10).mean()- A2交易量除以过去10日移动平均交易量
A2=td['Idxtrd06'].values/td['Idxtrd06'].rolling(10).mean()- A3收益率
A3=td['Idxtrd08'].values- A4最高价除以过去10日移动平均收盘价
A4=td['Idxtrd03'].values/td['Idxtrd05'].rolling(10).mean()- A5最低价除以过去10日移动平均收盘价
A5=td['Idxtrd04'].values/td['Idxtrd05'].rolling(10).mean()- A6极差
A6=td['Idxtrd03'].values-td['Idxtrd04'].values #极差,最高价-最低价- A7当天收益
A7=td['Idxtrd05'].values-td['Idxtrd02'].values #当天收益,收盘价-开盘价- 将数据保存为字典形式
X = {'A1':A1,'A2':A2,'A3':A3,'A4':A4,'A5':A5,'A6':A6,'A7':A7}- 将数据转化成数据框
X = pd.DataFrame(X) # 转化成数据框- 数据切片,从第10行开始到最后一行
X = X.iloc[9:-1,]- 后一日收盘价-前一日
Y = td['Idxtrd05'].values[1:] - td['Idxtrd05'].values[:-1] 最终得到以下标准的数据结构形式:
取后30行数据作为测试样本,剩下数据的作为训练样本,分别利用神经网络、支持向量机、逻辑回归模型进行训练及测试,分别获得对应模型的准确率和预测准确率。
(四)计算决策变量Y和上涨下跌的天数
- 注意错位相减的行数
Y=Y[9:] - 后一日收盘价-前一日收盘价大于0,表示上涨,记为1
Y[Y>0]=1 - 后一日收盘价-前一日收盘价小于0,表示下跌,记为-1
Y[Y<=0]=-1- 调整Y为len(Y)行1列
Y=Y.reshape(len(Y),1)- 求和统计上涨下跌的天数
counter_dict={}
Y_num=list(map(int,np.array(Y)))
for item in Y_num:
if item in counter_dict:
counter_dict[item] += 1
else:
counter_dict[item] = 1
print("上涨的天数:",counter_dict[1])
print("下跌的天数:",counter_dict[-1])(五)划分训练集和测试集
x_train=X.iloc[:len(X)-30,:] # 训练集的自变量
Y_train=Y[:len(Y)-30] # 训练集的因变量
x_test=X.iloc[len(X)-30:,:] # 测试集的自变量
Y_test=Y[len(Y)-30:] # 测试集的因变量(六)支持向量机
1.原理
SVM模型是一个比较基础的逻辑回归模型,也属于监督学习类的预测模型。简单来讲,就是找到一个面,把空间中的离散的点分开成两个区域。而SVM模型的核方法可以用来进行非线性的分类,换句话说,就是可以找到一个曲面来切割这个空间,而不是平面。 kernel:核函数的类型,一般常用的有’rbf’,’linear’,’poly’,等如图4-1-2-1所示,发现使用rbf参数时函数模型的拟合效果最好。
2.代码
- 导入SVM包
from sklearn import svm- 使用rbf参数时函数模型的拟合效果最好
clf = svm.SVC(kernel='rbf')- 将数组拉成一维数组
Y_train = Y_train.ravel()- 监督学习算法用训练数据拟合分类器模型
clf.fit(x_train, Y_train)- 计算模型准确率(针对训练数据)
rv1=clf.score(x_train, Y_train)- 用训练好的分类器去预测
R=clf.predict(x_test)- 调整Y为len(Y)行1列
R=R.reshape(len(R),1)- 计算预测准确率
Z=R-Y_test
Rs1=len(Z[Z==0])/len(Z)(七)逻辑回归
1.原理
logistic回归是一种广义线性回归(generalized linear model),因此与多重线性回归分析有很多相同之处。它们的模型形式基本上相同,都具有 w’x+b,其中w和b是待求参数,其区别在于他们的因变量不同,多重线性回归直接将w’x+b作为因变量,即y =w’x+b,而logistic回归则通过函数L将w’x+b对应一个隐状态p,p =L(w’x+b),然后根据p 与1-p的大小决定因变量的值。如果L是logistic函数,就是logistic回归,如果L是多项式函数就是多项式回归。
logistic回归的因变量可以是二分类的,也可以是多分类的,但是二分类的更为常用,也更加容易解释,多类可以使用softmax方法进行处理。实际中最为常用的就是二分类的logistic回归。
Logistic回归模型的适用条件
1 因变量为二分类的分类变量或某事件的发生率,并且是数值型变量。但是需要注意,重复计数现象指标不适用于Logistic回归。
2 残差和因变量都要服从二项分布。二项分布对应的是分类变量,所以不是正态分布,进而不是用最小二乘法,而是最大似然法来解决方程估计和检验问题。
3 自变量和Logistic概率是线性关系
4 各观测对象间相互独立。
原理:如果直接将线性回归的模型扣到Logistic回归中,会造成方程二边取值区间不同和普遍的非直线关系。因为Logistic中因变量为二分类变量,某个概率作为方程的因变量估计值取值范围为0-1,但是,方程右边取值范围是无穷大或者无穷小。所以,才引入Logistic回归。
2.代码
- 导入逻辑回归包
from sklearn.linear_model import LogisticRegression as LR- 创建逻辑回归模型类
lr = LR() - 将数组拉成一维数组
Y_train = Y_train.ravel()- 训练数据
lr.fit(x_train, Y_train) - 计算模型准确率(针对训练数据)
rv2=lr.score(x_train, Y_train); - 用训练好的分类器去预测
R=lr.predict(x_test)- 调整R为len(R)行1列
R=R.reshape(len(R),1)- 计算预测准确率
Z=R-Y_test
Rs2=len(Z[Z==0])/len(Z)(八)神经网络
1.原理
人工神经元被用来模拟神经元细胞的行为,神经元主要做了两部分的工作:首先对于输入信号进行综合,其次通过综合后的信号进行处理,得到输出信号。信号的综合,常用的方法是对输入信号加权求和。信号的处理,常用的方法是通过sigmoid函数处理。
sigmoid函数的表达式为g(z)=1/(1+e−z)g(z)=1/(1+e−z),可以看出,sigmoid函数的处理结果和真实神经元的处理结果比较类似(sigmoid函数值集中于1和0,对应于神经元细胞的兴奋和不兴奋状态),而且sigmoid函数可以根据函数值很容易的得到导数值。
人工神经网络其实是真实神经网络的简化
神经网络由三层组成,输入层,隐含层,输出层。需要注意的是,输入层和输出层都只有一层结构,隐含层可以是一层,也可以包含多层结构。
这个神经网络可以用来计算异或。异或是一种运算:如果输入的a、b两个值不相同,则异或结果为1。如果输入的a、b两个值相同,异或结果为0。
当输入的x1=1,x2=1的时候:
a1=1⋅(−30)+x1⋅20+x2⋅20=1⋅(−30)+1⋅20+1⋅20=10a1=1⋅(−30)+x1⋅20+x2⋅20=1⋅(−30)+1⋅20+1⋅20=10
z1=sigmoid(a1)≈1z1=sigmoid(a1)≈1
a2=1⋅10+x1⋅(−20)+x2⋅(−20)=1⋅(10)+1⋅(−20)+1⋅(−20)=−30a2=1⋅10+x1⋅(−20)+x2⋅(−20)=1⋅(10)+1⋅(−20)+1⋅(−20)=−30
z2=sigmoid(a2)≈0z2=sigmoid(a2)≈0
s1=1⋅(10)+z1⋅(−20)+z2⋅(−20)=1⋅(10)+1⋅(−20)+0⋅(−20)=−10s1=1⋅(10)+z1⋅(−20)+z2⋅(−20)=1⋅(10)+1⋅(−20)+0⋅(−20)=−10
y1=sigmoid(s1)≈0y1=sigmoid(s1)≈0
同理,当x1=1,x2=0的时候,y1=1;
当x1=0,x2=1的时候,y1=1;
当x1=0,x2=0的时候,y1=0。
2.代码
- 导入逻辑回归包
from sklearn.neural_network import MLPClassifier- 创建神经网络分类器对象
clf = MLPClassifier(solver='lbfgs', alpha=1e-5,hidden_layer_sizes=(5,2), random_state=1)- 将数组拉成一维数组
Y_train = Y_train.ravel()- 训练数据
clf.fit(x_train, Y_train);- 计算模型准确率(针对训练数据)
rv3=clf.score(x_train, Y_train)- 用训练好的分类器去预测
R=clf.predict(x_test)- 调整R为len(R)行1列
R=R.reshape(len(R),1)- 计算预测准确率
Z=R-Y_test
Rs3=len(Z[Z==0])/len(Z)(九)数据可视化
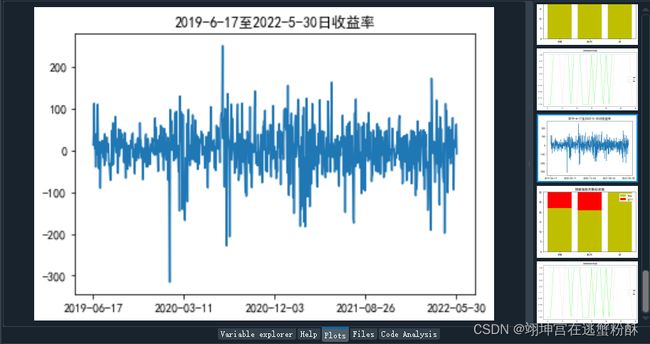
- 收益率可视化
x = A8[9:-1]
y = Y # 使用Matplotlib画折线图
plt.plot(x, y)
plt.gca().xaxis.set_major_locator(ticker.MultipleLocator(179))#显示坐标轴更美观
plt.title('2019-6-17至2022-5-30日收益率')
plt.show()- 预测涨跌天数柱状图
######预测后的涨跌柱状图######
name_list = [
'SVM',
'MLPC',
'LR']
num_list = [
counter_dict1[1],
counter_dict2[1],
counter_dict3[1]]
num_list1 = [
counter_dict1[-1],
counter_dict2[-1],
0]
plt.bar(range(len(num_list)), num_list, label='boy',fc ='y')
plt.bar(range(len(num_list)), num_list1, bottom=num_list, label=
'girl',tick_label = name_list,fc =
'r')
plt.legend()
plt.title('预测涨跌天数柱状图')
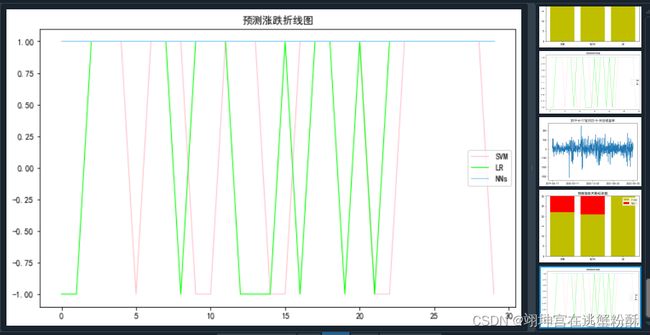
plt.show()- 预测涨跌天数折线图
#######预测后的涨跌折线图#######
x_ticks = np.arange(len(R1))# x轴刻度标签
x = np.arange(len(x_ticks))
y1=R1# 第1条折线数据
y2=R2# 第2条折线数据
y3=R3# 第3条折线数据
plt.figure(figsize=(10, 6))
plt.plot(x, y1, color='#FFC0CB', label='SVM', linewidth=1.0)# 画第1条折线
plt.plot(x, y2, color='#00FF00', label='LR', linewidth=1.0)# 画第2条折线
plt.plot(x, y3, color='#87CEFA', label='NNs', linewidth=1.0)# 画第3条折线
plt.title('预测涨跌折线图')# 标题
plt.legend()# 图例
plt.show()# 显示图片四、系统测试与运行结果
(一)系统测试方法
进行系统测试的原因是尽可能的找到系统中存在的错误,包括运行的错误和个别的数据不能录入等,通过找出这些错误然后尽可能的改正,最终使完成的系统能够趋近完美。本系统的测试由小模块逐渐到整体,测试步骤如下:
1.单元测试
该测试在编码阶段进行,完成一个功能后进行调试查看能否运行,运行结果是否正确。
2.集成测试
该测试是在单元测试完成后进行的,是将各个功能模块组合成一个完整的系统后查看是否存在错误。
3.确认测试
该测试是在完整的系统能够运行后进行,目的是查看系统功能是否符合预期。
4.系统测试
该测试是将软硬件及操作人员等作为一个整体进行测试。
(二)本系统测试结果
本节通过对各个模块进行测试,检验各功能是否可以使用。
- 数据处理
- 计算决策变量Y和上涨下跌的天数
- 划分训练集和测试集
- 支持向量机
- 逻辑回归
- 神经网络
五、结 论
本程序设计充分利用了机器学习的有关知识,用支持向量机、逻辑回归、神经网络预测股票的涨跌,并可视化,最终实现了原本预期的效果。
由于本人开发知识和经验不足,开发时间有限,使得系统存在着一些不足之处,如可视化设计不够美观、程序框架结构不够严密等,日后会弥补这些不足之处,使得系统在未来更加完善。
参考文献
- [1]专著:黄恒秋、张良均、谭立云、莫洁安著,Python金融数据分析与挖掘实战[M],北京:人民邮电出版社,2020年1月。
六、源代码
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib import pyplot as ticker
######读取数据&数据处理######
td=pd.read_excel('hs300.xlsx') # 读取数据
td.head(6) # 查看前6行
A1=td['Idxtrd05'].values/td['Idxtrd05'].rolling(10).mean() #收盘价除以过去10日移动平均收盘价
A2=td['Idxtrd06'].values/td['Idxtrd06'].rolling(10).mean() #交易量除以过去10日移动平均交易量
A3=td['Idxtrd08'].values # 收益率
A4=td['Idxtrd03'].values/td['Idxtrd05'].rolling(10).mean() #最高价除以过去10日移动平均收盘价
A5=td['Idxtrd04'].values/td['Idxtrd05'].rolling(10).mean() #最低价除以过去10日移动平均收盘价
A6=td['Idxtrd03'].values-td['Idxtrd04'].values #极差,最高价-最低价
A7=td['Idxtrd05'].values-td['Idxtrd02'].values #当天收益,收盘价-开盘价
A8=td['Idxtrd01'].values # 收益率
X = {'A1':A1,'A2':A2,'A3':A3,'A4':A4,'A5':A5,'A6':A6,'A7':A7} # 保存成字典形式
X = pd.DataFrame(X) # 转化成数据框
X.head(6)
X = X.iloc[9:-1,] #数据切片,从第10行开始到最后一行
Y = td['Idxtrd05'].values[1:] - td['Idxtrd05'].values[:-1] #后一日收盘价-前一日收盘价
Y=Y[9:] # 注意错位相减的行数
#######可视化收益率#####
x = A8[9:-1]
y = Y # 使用Matplotlib画折线图
plt.plot(x, y)
plt.gca().xaxis.set_major_locator(ticker.MultipleLocator(179))#显示坐标轴更美观
plt.title('2019-6-17至2022-5-30日收益率')
plt.show()
#######数据准备########
Y[Y>0]=1 # 后一日收盘价-前一日收盘价大于0,表示上涨,记为1
Y[Y<=0]=-1 # 后一日收盘价-前一日收盘价小于0,表示下跌,记为-1
Y=Y.reshape(len(Y),1)#4.调整Y为len(Y)行1列
counter_dict={}
Y_num=list(map(int,np.array(Y)))
for item in Y_num:
if item in counter_dict:
counter_dict[item] += 1
else:
counter_dict[item] = 1
print("上涨的日数:",counter_dict[1])
print("下跌的日数:",counter_dict[-1])
#######划分训练集和测试集########
x_train=X.iloc[:len(X)-30,:] # 训练集的自变量
Y_train=Y[:len(Y)-30] # 训练集的因变量
x_test=X.iloc[len(X)-30:,:] # 测试集的自变量
Y_test=Y[len(Y)-30:] # 测试集的因变量
###### SVM #########
from sklearn import svm
clf = svm.SVC(kernel='rbf')#使用rbf参数时函数模型的拟合效果最好。
Y_train = Y_train.ravel() #将数组拉成一维数组
clf.fit(x_train, Y_train)
rv1=clf.score(x_train, Y_train)
R1=clf.predict(x_test)
R1=R1.reshape(len(R1),1)
Z1=R1-Y_test
Rs1=len(Z1[Z1==0])/len(Z1)
counter_dict1={}
R1_num=list(map(int,np.array(R1)))
for item1 in R1_num:
if item1 in counter_dict1:
counter_dict1[item1] += 1
else:
counter_dict1[item1] = 1
#########逻辑回归##########
from sklearn.linear_model import LogisticRegression as LR
lr = LR() #创建逻辑回归模型类
Y_train = Y_train.ravel()
lr.fit(x_train, Y_train) #训练数据
rv2=lr.score(x_train, Y_train); # 模型准确率(针对训练数据)
R2=lr.predict(x_test)
R2=R2.reshape(len(R2),1)
Z2=R2-Y_test
Rs2=len(Z2[Z2==0])/len(Z2)
counter_dict2={}
R2_num=list(map(int,np.array(R2)))
for item2 in R2_num:
if item2 in counter_dict2:
counter_dict2[item2] += 1
else:
counter_dict2[item2] = 1
##########神经网络########
from sklearn.neural_network import MLPClassifier
clf = MLPClassifier(solver='lbfgs', alpha=1e-5,hidden_layer_sizes=(5,2), random_state=1)#(2).创建神经网络分类器对象
Y_train = Y_train.ravel()
clf.fit(x_train, Y_train);
rv3=clf.score(x_train, Y_train)
R3=clf.predict(x_test)
R3=R3.reshape(len(R3),1)
Z3=R3-Y_test
Rs3=len(Z3[Z3==0])/len(Z3)
counter_dict3={}
R3_num=list(map(int,np.array(R3)))
for item3 in R3_num:
if item3 in counter_dict3:
counter_dict3[item3] += 1
else:
counter_dict3[item3] = 1
#####输出预测结果######
print('支持向量机模型准确率:',rv1)
print('逻辑模型准确率:',rv2)
print('神经网络模型准确率:',rv3)
print('---------------------------------------------')
print('支持向量机模型预测准确率:',Rs1)
print('逻辑模型预测准确率:',Rs2)
print('神经网络模型预测准确率:',Rs3)
######预测后的涨跌柱状图######
name_list = [
'SVM',
'MLPC',
'LR']
num_list = [
counter_dict1[1],
counter_dict2[1],
counter_dict3[1]]
num_list1 = [
counter_dict1[-1],
counter_dict2[-1],
0]#神经网络预测的只有上涨
plt.bar(range(len(num_list)), num_list, label='rise',fc ='y')
plt.bar(range(len(num_list)), num_list1, bottom=num_list, label=
'fall',tick_label = name_list,fc =
'r')
plt.legend()
plt.title('预测涨跌天数柱状图')
plt.show()
#######预测后的涨跌折线图#######
x_ticks = np.arange(len(R1))# x轴刻度标签
x = np.arange(len(x_ticks))
y1=R1# 第1条折线数据
y2=R2# 第2条折线数据
y3=R3# 第3条折线数据
plt.figure(figsize=(10, 6))
plt.plot(x, y1, color='#FFC0CB', label='SVM', linewidth=1.0)# 画第1条折线
plt.plot(x, y2, color='#00FF00', label='LR', linewidth=1.0)# 画第2条折线
plt.plot(x, y3, color='#87CEFA', label='NNs', linewidth=1.0)# 画第3条折线
plt.title('预测涨跌折线图')# 标题
plt.legend()# 图例
plt.show()# 显示图片