GCAN: Graph Convolutional Adversarial Network for Unsupervised Domain Adaptation

GCAN: Graph Convolutional Adversarial Network for Unsupervised Domain Adaptation

摘要

连接源域和目标域的三种类型可利用信息

1. 数据结构
2. 域标签
3. 类标签

提出：用于无监督领域自适应的端到端图卷积对抗网络
第一个在无监督领域自适应的深度模型中联合建模这三种信息的工作。
设计了三种有效对齐机制，学习域不变表示和语义表示，减少域自适应的域差异

介绍

深度学习所需的大量标注数据难以获得——利用已有标注数据——存在数据集偏差和域漂移现象——大规模数据集训练的预测模型难以很好地推广到新的数据集和任务（受不同领域数据分布的影响）——领域自适应（在训练和测试分布之间存在漂移的情况下，学习一个鉴别分类器或其他预测器）
领域自适应
主要技术困难：如何正式减少不同领域的分布差异
领域自适应方法分类：
基于实例的领域自适应
基于参数的领域自适应
基于特征的领域自适应

差异度量
MMD
对抗领域适应方法

三类信息

    数据结构
        反映了数据集的固有属性，包括边际或条件数据分布、数据统计信息、几何数据结构等。

    域标签
        用于对抗性领域自适应方法，帮助训练域分类器建模源域和目标域全局分布

    类标签
        特别是目标伪标签，通常采用强制语义对齐，保证来自具有相同类标签的不同域的样本将被映射到特征空间附近。

    总结：三种类型信息都有助于减少不同方面的领域差异，相互补充和增强领域自适应

以前的方法
  深度对抗领域自适应，只强制全局域统计的对齐，类别的关键语义类标签信息可能会丢失，不能保证来自具有相同类标签的不同域的样本将被映射到特征空间的附近。（对齐错了）
  语义迁移方法，将类标签信息传播到深度对抗性自适应网络中，以解决上述局限性。
  传统的数据结构相关方法，在保持原始空间中的数据属性的同时，减少域之间的分布差异。难以建模和将数据结构信息有效集成到现有的深度网络中

结构感知对齐
  利用源域和目标域的数据结构，使结构最小化结构差异，减少域偏移。
建模深度网络下的数据结构
  （1）利用样本的CNN特征，基于样本结构相似性，构造一个密集连接的实例图。每个节点对应于一个样本的CNN特征（由一个标准的卷积网络提取，如AlexNet）
  （2）在实例图上应用图卷积网络（GCN），使结构信息沿加权图边传播，可以从设计的网络中学习到。

域对齐
  挖掘来自不同域的全局域统计信息以相互匹配。利用由对抗性相似度损失来度量的域统计量的散度来指导特征提取器学习域不变表示。

类质心对齐
  约束来自不同域的类质心，随着迭代的增加而靠近，以便学习的表示可以用类标签信息进行编码。因此，具有相同类别标签的样本可以嵌入到特征空间附近。模型通过进行类对齐损失来实现该想法，并采用移动质心策略来抑制虚假伪标签的影响。

  通过对这三种对齐机制的建模，深度网络可以生成域不变的和可区分的语义表示。

相关工作

领域自适应
三种方法
分布度量
MMD
对抗性目标

图神经网络
  在非结构数据上使用深度学习框架，卷积网络在非欧几里得图的自然推广
GNN首次提出是作为一种可训练的循环消息传递
在图上构造GCN的两个流：
光谱透视图，其中图卷积的局域性以光谱分析的形式被考虑。
空间透视图，其中卷积滤波器直接应用于图节点及其邻居
本文工作是基于光谱透视线，模型利用GCN在密集连接的实例图上操作，在统一的深度网络中的数据结构信息与域标签和类标签信息共同补充。

图卷积对抗网络

图卷积对抗网络
损失函数
通过最小化下面的总体目标函数来训练标签预测函数f
$\begin{array}{rl}\mathcal{L}\left({\mathcal{X}}_S,{\mathcal{Y}}_S,{\mathcal{X}}_T\right)& ={\mathcal{L}}_C\left({\mathcal{X}}_S,{\mathcal{Y}}_S\right)+\lambda {\mathcal{L}}_{DA}\left({\mathcal{X}}_S,{\mathcal{X}}_T\right)\\ & +\gamma {\mathcal{L}}_{CA}\left({\mathcal{X}}_S,{\mathcal{Y}}_S,{\mathcal{X}}_T\right)+\eta {\mathcal{L}}_T\end{array}$
分类损失函数：${\mathcal{L}}_{\mathcal{C}}({\mathcal{X}}_{\mathcal{S}},{\mathcal{Y}}_{\mathcal{S}})={\mathbb{E}}_{(x,y)\sim D_S}\left[J(f(x),y)\right],J(\cdot ,\cdot )$为交叉熵损失
$\lambda ,\gamma ,\eta 为平衡参数,{\mathcal{L}}_{{\mathcal{D}}_{\mathcal{C}}}$,${\mathcal{L}}_{{\mathcal{C}}_{\mathcal{A}}},{\mathcal{L}}_{\mathcal{T}}$,分别表示域对齐损失，类对齐损失，结构感知的triple loss

域对齐
使用域对抗的相似性损失作为域对齐损失
域判别器D,特征提取器G,二者博弈，当G提取到域不变特征时达到一个平衡
$\begin{array}{rl}{\mathcal{L}}_{DA}\left({\mathcal{X}}_S,{\mathcal{X}}_T\right)& ={\mathbb{E}}_{x\in D_S}[\log (1-D(G(x)))]\\ & +{\mathbb{E}}_{x\in D_T}[\log (D(G(x)))]\end{array}$

结构感知对齐
基本思想
  域对齐机制只强制执行全局域统计信息的对齐，而忽略了小批量样本的结构信息。
  （1）使用数据结构分析器（DSA）网络来为一个小批量样本生成结构分数
  （2）利用结构分数和学习到的样本的CNN特征构造密集连接的实例图
  （3）在实例图上操作图卷积网络（GCN），学习用数据结构信息编码的GCN特征

GCN（基本）
  GCN的目的是学习可以直接应用于图上的分层传播操作。
  给定一个有m个节点的无向图，节点间的边的集合，和一个邻接矩阵$A\in R^{m\times m}$
   图卷积的线性变换表示为图信号$X\in R^{k\times m}（列向量X_i\in R^k$，是第i个节点的特征表示）与滤波器$W\in R^{k\times c}$的乘积：
$\mathbf{Z}={\hat{\mathbf{D}}}^{-\frac{1}{2}}\hat{\mathbf{A}}{\hat{\mathbf{D}}}^{-\frac{1}{2}}{\mathbf{X}}^T\mathbf{W}$
$\hat{\mathbf{A}}=\mathbf{A}+\mathbf{I},{\hat{\mathbf{D}}}_{ii}={\sum }_j^{}{\hat{\mathbf{A}}}_{ij}$，输出$\mathbf{Z}$是一个$c\times m$的矩阵
  请注意，GCN可以通过堆叠多个图卷积层来构建，如公式（4）中的形式，并且每层后面都有一个非线性运算（如ReLU）。

为GCN构架密集连接的实例图
即上述等式中的图信号X和邻接矩阵A
  实例图中的每个节点代表一个样本的特征，该特征由一个标准的卷积网络提取，例如，AlexNet或VGG。因此，图信号X可以通过：
$\mathbf{X}=CNN({\mathbf{X}}_{batch}),{\mathbf{X}}_{batch}$表示一个mini-batch的样本
为构建邻接矩阵$\hat{\mathbf{A}}$,相同的mini-batch样本被喂到DSA网络中生成结构分数${\mathbf{X}}_{sc}$,从而邻接矩阵可以构建为：
$\hat{\mathbf{A}}={\mathbf{X}}_{sc}{\mathbf{X}}_{sc}^T,{\mathbf{X}}_{sc}\in R^{w\times h}$,w是batch size，h是结构分数的维度，值得注意的是结构分数可以进一步受到Triple Loss损失的限制（通过指导数据结构分析器网络对数据样本的结构相似性信息进行建模，生成结构分数。）：
${\mathcal{L}}_T=\max \left({\Vert {\mathbf{X}}_{s{c}_a}-{\mathbf{X}}_{s{c}_p}\Vert }^2-{\Vert {\mathbf{X}}_{s{c}_a}-{\mathbf{X}}_{s{c}_n}\Vert }^2+{\alpha }_T,0\right)$
${\mathbf{X}}_{s{c}_a}$是从源域随机采样的，${\mathbf{X}}_{s{c}_p}$是从${\mathbf{X}}_{s{c}_a}$的相同类别中选择的,${\mathbf{X}}_{s{c}_n}$是来自不同的类别
阈值${\alpha }_T$是一个边际。给定图信号$\mathbf{X}$和邻接矩阵$\hat{\mathbf{A}}$,可以根据（4）获得GCN特征
  由于源CNN特征和目标CNN特征在早期训练中具有域判别性，同时构造图可能会影响网络训练的稳定性。因此，源图和目标图被单独构造并输入参数共享的GCNs来学习表示。

类对齐
  域不变性和结构一致性不等于可鉴别性。
  ｜ 例如，目标类别“笔记本电脑”的特征可以在满足域不变性和结构一致性条件的同时，映射到源类别“屏幕”的特征附近。 ​
  通过类质心对齐来为UDA的类标签信息进行建模
  ｜ 研究表明，监督域适应(SDA)方法利用类标签信息改进了非监督域适应(UDA)，因为SDA可以确保来自不同域的同一类的特征被映射到附近。
首先，使用目标分类器F来分配伪标签，然后得到一个伪标记的目标域，被标记的样本和伪标记的样本一起用于计算每个类的质心。
  无监督域自适应的质心对齐目标如下：
${\mathcal{L}}_{CA}\left({\mathcal{X}}_S,{\mathcal{Y}}_S,{\mathcal{X}}_T,{\mathcal{Y}}_T\right)={\sum }_{k=1}^K\varphi \left({\mathcal{C}}_S^k,{\mathcal{C}}_T^k\right)$
${\mathcal{C}}_S^k和{\mathcal{C}}_T^k$是源域和目标域中类别k的质心,$\Phi (\cdot ,\cdot )$是任何适当的距离度量函数，本论文实验里使用的是$\varphi \left(x,x^{\prime }\right)={\Vert x-x^{\prime }\Vert }^2$,平方欧几里得距离，通过显式地限制来自不同域的类质心之间的距离，可以确保在同一个类中的特征将被映射到附近。
网络结构图
  在结构感知对齐中，数据结构分析器网络产生了用源数据结构信息编码的结构分数，而CNN特征是由CNN提取的。然后，结构分数和CNN特征被用来为GCN构建密集连接的实例图。经过串联的CNN和GCN特征被输入到域对齐和类中心点对齐模块。在域对齐中，应用域对齐损失来匹配全局域统计。在类中心点对齐中，伪标记的目标特征和标记的源特征被用来计算类中心点对齐损失，以确保来自不同领域的同一类别的样本可以紧密嵌入。

实验

Office-31
三个不同领域的31个类别中的4110张图像
ImageCLEF-DA
3个域12个类别，每个类别50张，每个域600张
Office-Home
4个域12个任务，65个类别
Baseline Methods
  在Office-31和ImageCLEF-DA数据集上，首先使用一个基于源数据训练的站立深度学习网络，例如，Alexnet，来预测目标数据上的样本，这提供了一个较低的目标性能界(不做领域自适应直接应用)。然后，与最先进的迁移学习方法进行了比较.所有的基线结果都直接引用自这些已发表的论文。
Office-Home上主要比较了7种最先进的浅层领域自适应方法.进一步比较了几种深度领域自适应模型。所有的结果都直接引用，除了MSTN的结果是通过自己运行发布的代码2获得的。

Implementation Details
  遵循与论文中相同的无监督领域自适应的标准评估协议。使用所有有标记的源样本和所有未有标记的目标样本。重复每个转移任务三次，并报告平均精度和标准误差。
Network Architecture
  模型主要有四个模块，即CNN、数据结构分析器(DSA)、域分类器和GCNs。对于cnn，在所有的实验中都采用了AlexNet架构。在RTN和Revgral之后，在AlexNet中的fc7层之后添加了一个包含256个单元的瓶颈层fcb。为了与其他方法进行公平的比较，还在预训练的AlexNet模型中微调了conv1、v2、v3、conv5、fc6、fc7层。
  数据结构分析器(DSA)是实现为原始的预训练的AlexNet，具有一个1000维的输出。在Triple Loss损失训练中对源数据进行微调。对于GCNs的体系结构，只使用一个GCN。节点表示的维数为256，输出维数为150。对于域分类器，使用与RevGrad[22]相同的架构，即x→1024→1024→1。辍学策略也被使用。在的实现中，所有的模型和方法都是使用张量流来实现的。

Results and Analysis
  在Office-31和ImageCLEF-DA数据集上
  模型在大多数迁移任务上的性能都优于所有的比较方法。值得注意的是，所提出的GCAN可以有效地改善包括A→W、A→D、W→A和D→A这四个困难迁移任务。
  （1）的深度迁移学习方法优于标准的深度学习方法，例如，AlexNet。它验证了域转移不能被深度网络消除。
  （2）DRCN训练了一个额外的解码器来强制执行包含语义信息的提取特征，从而比Alexnet高约4%。这一改进也表明了学习语义表示的重要性。
  （3）另外，分布匹配方法RevGrad、RTN和JAN也比仅对源数据进行训练的AlexNet带来了显著的改进。的方法以一种非常简单的形式利用了DRCN和分布匹配方法的优点。特别是，与使用解码器来提取语义信息相比，的方法通过类质心对齐来利用类标签信息，从而将来自不同域的相同类中的特征映射到附近。
  （4）与最先进的MSTN相比，GCAN显著提高了性能，这证明了在深度网络中建模数据结构以进行领域自适应的有效性。
Office-Home.
  所提出的模型在所有迁移任务上都大大优于所有基线方法，甚至超过了最近最先进的MSTN约3%。从研究结果来看，有了以下的观察结果。（1）与PUnDA和DAN等浅层方法和深度方法相比，PUnDA和DAN的性能近似处于同一水平，这证实了数据结构匹配在领域自适应问题中是至关重要的。
  不仅能够学习一般视觉任务的表征，还能够学习领域适应的可转移表征。值得注意的是，所有的方法都使用VGG作为其基本的特征提取器，而MSTN和GCAN则使用AlexNet进行特征提取。令人惊讶的是，MSTN和GCAN仍然可以超越其他浅层和深层的方法，这可以验证类质心对齐的强大能力。

Further Remarks
  由于模型涉及到对抗性自适应模块，=从两个不同的方面证明了它对收敛的性能。首先是测试精度，模型的收敛速度与RevGrad相似。
  （1）与传统GANs中的消失发生器梯度问题不同，由对抗性自适应方法生成的特征所在的流形似乎是完全对齐的。因此，特征提取器的梯度不会消失，而是会导致JS距离的减小。这证明了对抗性领域自适应方法的可行性。（2）与RevGrad相比，模型更稳定，可以加速JSD的最小化过程。这表明，方法通过三种对齐机制稳定了著名的不稳定对抗性训练。

网络结构图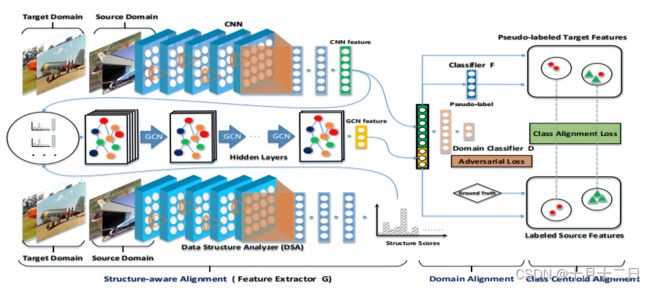
CNN模块用于提取样本特征（图信号），DSA用于获取结构分数，构造邻接矩阵，利用图信号和邻接矩阵实现GCN图卷积操作，获得图卷积后的输出表示与之前CNN提取的特征进行拼接，进行后续的域对齐和类质心对齐操作。

论文链接
知识拓展
图卷积网络
Triple Loss