AAAI——Disentangled Multi-Relational Graph Convolutional Network for Pedestrian Trajectory Prediction

用于行人轨迹预测的分解多关系图卷积网络

论文来源：AAAI 2021
论文链接：https://www.aaai.org/AAAI21Papers/AAAI-1677.BaeI.pdf
代码链接：无

---

摘要

行人轨迹预测是人类环境中自主导航和社交机器人所需的重要任务之一。以前的研究集中在估计单个行人的社会力量上。然而，他们没有考虑行人群体的社会力量，这导致了过度碰撞的避免问题。为了解决这个问题，我们提出了一个用于社会纠缠的行人轨迹预测的Disentangled Multi-Relational Graph Convolutional Network（DMRGCN）。我们首先介绍了一种新型的分解多尺度聚合，以更好地代表社会互动，在一个加权图上的行人之间。对于聚合，我们根据行人之间的距离和相对位移来构建多关系加权图。在预测步骤中，我们提出了一个全局性的时间聚合，以减轻行人改变方向时的累积误差。最后，我们将DropEdge应用到我们的DMRGCN中，以避免相对较小的行人轨迹数据集上的过拟合问题。通过在一个端到端的框架内有效地整合这三个部分，DMRGCN在各种具有挑战性的轨迹预测基准上实现了最先进的性能。

---

1.简介

行人轨迹预测试图根据人们以前的步骤来预测他们的路径，是自主导航和社会机器人平台的一个重要部分。它假定一个人朝着一个目的地行走，同时考虑到与其他人的互动。具体来说，行人通过选择最佳路线与同伴一起移动，以避免碰撞，并倾向于跟随他们周围人流的脚步。(Helbing and Molnar 1995; Mehran, Oyama, and Shah 2009)中的开创性工作将这些人与人之间的互动建模为社会力量。然而，社会力量依赖于参数化的模型，这些模型很难概括复杂的人际关系。
最近，卷积神经网络（CNN）的采用缓解了泛化的问题。Alahi等人在2016年的一项工作中介绍了一个Social-LSTM，它使用具有社会池的递归神经网络（RNNs）来预测人类的轨迹，以模拟相邻行人的互动。在（Gupta等人，2018）中，提出了一个基于生成对抗网络（GANs）的编码器-解码器框架，该框架有一个全局池化机制来学习社会规范。然而，我们观察到，学习轨迹所需的重要特征有时会通过启发式的池化方法泄露。
捕捉人类与相关邻居互动的另一种方法涉及学习一个图的表示，它由一组节点和边组成，（Kosaraju等人，2019；Mohamed等人，2020）。在行人轨迹预测中，节点代表场景中的每个行人，边则对应于与其他行人的距离。图卷积网络（GCN）的使用使其能够更好地学习行人之间的物理和社会互动。尽管基于GCN的工作在预测进一步的轨迹方面表现出很好的性能，但它们中的大多数都有两个限制。(1)只有简单的社会关系，如避免碰撞被汇总；(2)最终目的地不可避免地发生错误，因为社会规范的建模不适合在最后一帧中确定行人的终点。
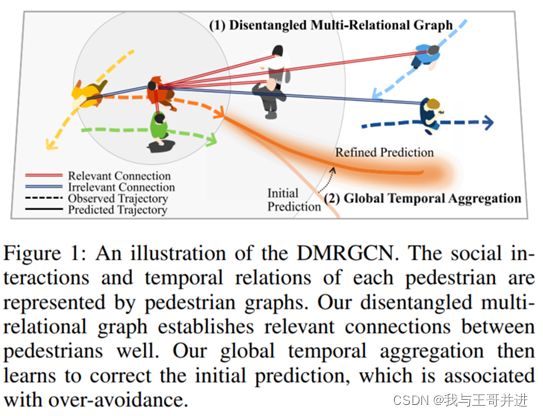
在本文中，我们提出了一个Disentangled Multi-Relational Graph Convolutional Network（DMRGCN），即图1中基于GCN的社会纠缠行人轨迹预测。我们的DMRGCN由三部分组成：用多关系图进行disentangled多尺度聚合，全球时间聚合和DropEdge应用于行人轨迹预测。
与之前基于GCN的方法（Mohamed等人，2020）相比，DMRGCN建立了复杂的社会关系模型。这是通过在多关系图上进行多尺度的分解聚合来实现的，多关系图表示行人之间的距离和相对位移。这是受行动识别的启发（Liu等人，2020），目的是消除图的冗余依赖。我们还利用我们的全局时间聚合，对过度规避引起的最终目的地误差进行补偿。我们在时间预测CNN的中间层提取一个运动特征，然后将该特征与它的输出相加。最后，我们将DropEdge（Rong等人，2020）应用到我们的DMRGCN中，它在每个训练周期随机地从输入图中删除一定数量的边，以避免在相对较小的行人轨迹数据集上出现过拟合问题。通过对这些设计的有效整合，我们的模型在轨迹预测的准确性上优于以往的模型。

---

2.相关的工作

在本节中，我们将简要回顾用于行人轨迹预测的各种方法。

2.1 行人轨迹预测。

开拓性的工作（Helbing和Molnar 1995；Pellegrini等人2009；Mehran, Oyama和Shah 2009；Yamaguchi等人2011）使用了基于社会力量的手工能量势。此后，随着CNN和RNN的引入，行人轨迹预测的最先进技术得到了发展。Social-LSTM（Alahi等人，2016）提出了一个具有社会集合的RNN模型，该模型将邻居行人聚集在一个网格上。Social-Attention（Vemula、Muelling和Oh 2018）、SR-LSTM（Zhang等人2019）和SFT（Fernando等人2018）用新的集合方案扩展了社会集合的能力，它不仅使用网格内的人，还使用所有行人，其重要性由注意力模块加权计算。Shi等人（2020）的一项工作使用注意力模块汇总了行人与其他人的关系，并使用高斯混合模型预测了行人接下来会采取的坐标。SocialGAN（Gupta等人，2018）引入了一个生成模型来预测社会上可接受的路径。它的生成器以多模式的方式递归预测轨迹，而判别器则对预测的路径是真还是假进行分类。SoPhie（Sadeghian等人，2019）通过分别引入物理和社会关注，捕捉到人与人和人与环境的互动。在（Sun, Zhao, and He 2020）中，一个强制执行前向和后向路径预测一致性的互惠学习也显示了合理的性能。更多信息，我们将读者引导到（Bartoli等人，2018；Rehder和Kloeden，2015；Rehder等人，2018；Liang等人，2019）的条件性轨迹预测，这不在本文的范围之内。

2.2 基于图神经网络的方法。

随着图神经网络在各种关系建模应用中的成功，如节点分类（Kipf and Welling 2017; Hamilton, Ying, and Leskovec 2017; Xu et al. 2019; Velickovi ˇ c et al. 2018; Li et al. 2019b）和动作`识别（Yan, Xiong, and Lin 2018; Li et al.2019c; Shi et al. 2019b,a; Li et al. 2019a; Liu et al. 2020），很明显，社会关系也可以在图上表示，这使得行人轨迹预测更容易操作（Huang et al. 2019; Kosaraju et al. 2019; Mohamed et al. 2020）。
在（Velickovi ˇ c等人2018）中，通过隐式分配每个节点的重要性，将图注意网络（GAT）应用于基于自我注意的架构中。对于行人轨迹预测的应用，图结构被直接用于更好地学习行人之间的物理和社会互动（Huang等人，2019）。SocialBiGAT（Kosaraju等人，2019）将GAT纳入BicycleGAN（Zhu等人，2017），以调整每个行人的潜在向量，消除路径预测的不必要的退化。在（Liang等人，2020）中，GAT被用在二维网格图上，用于多个合理的目的地预测。作为最近的进展，Social-STGCNN（Mohamed等人，2020）使用GCN将运动信息聚集在由每个时域的图形堆叠而成的时空图上，其边缘由基于位移的核函数进行权重。然后通过一个时间卷积网络（TCN）一次性进行时间预测（Bai, Kolter, and Koltun 2018）。与Social-STGCNN相比，我们的DMRGCN也采用了GCN机制，但它可以利用多尺度聚合学习行人之间复杂的社会关系。此外，通过全局时间聚合的设计，它对减少长序列的累积误差非常有效。

---

3.分解的多关系图卷积网络

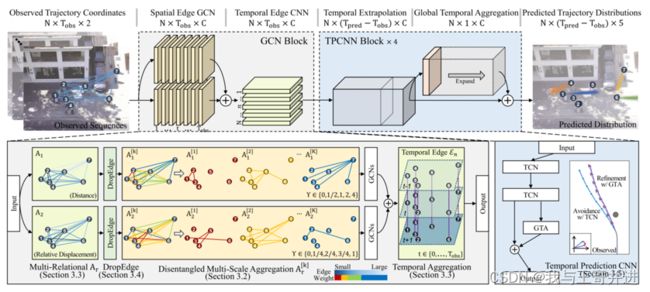
我们提出了一种端到端的行人轨迹预测方法。我们的贡献有三个方面。(1)一个分解的多尺度聚合，以明确区分相关的行人；(2)一个多关系的GCN，以提取场景中复杂的社会互动；(3)一个全局的时间聚合，以补偿过度回避的累积误差。图2显示了拟议模型的概况。

3.1 初步

问题的定义
行人轨迹预测问题涉及从观察到的位置序列中确定场景中所有人员的未来位置序列。假设一个场景中有N个行人，每个行人在特定时间t的相应位置可以表示为 使用观察到的时间帧Tobs和总序列帧 $T_{pred}$，行人的完整序列可以表示为 。我们假设预测的坐标 是随机变量。在所有行人的给定序列下 ，概率模型被学习来估计 行人在最后观察到的帧之后出行。

图卷积网络
图 表示为 ，其中V是N个节点的集合， 是代表节点之间联系的边的集合。空间-时间图表示为： 所有观察时间的空间 图的属性集合。节点特征 是一组行人的位置 $p_t^n$它的邻接矩阵 表示行人i和j之间的物理关系。层级GCN特征更新如下。

其中， 是关系图的归一化形式， 增加了自循环。 表示对角线节点程度矩阵，来自于 非线性激活函数（在我们的实现中是PReLU），而W表示层级可学习的权重矩阵。
对于最初 用于表示实体之间关系的多关系图（Marcheggiani和Titov 2017；Shi等人2019b；Li等人2019c）， 使用额外的术语来表示边的R关系。通过这些关系，一个邻接矩阵将关系信息表达为 多关系GCN的 逐层特征更新规则定义为

其中l是各层的索引。

3.2 分散的多尺度聚合

过度平滑和有偏见的加权问题
尽管基于图的方法可以很好地表示任意结构，但有两个问题限制了它们对行人轨迹预测的适用性。首先，它们受到节点特征的过度平滑问题的影响。当为拥挤的环境构建行人图时，由于大量节点的聚集，特征被平滑化了。
另一个问题来自于高阶社会关系。在（Li et al. 2019c）中，使用k-hop邻域的多尺度聚合进行特征聚合，其中邻域矩阵的k阶多项式 。采用多尺度聚合的GCN特征更新规则定义为

其中 表示多项式邻接矩阵的归一化项 。通过这种方式，可以通过在具有独立权重的远邻和近邻之间建立关系来学习丰富的表征。
我们试图将这一想法直接用于行人轨迹预测，但由于行人图的内在差异，存在一个问题。在为多尺度聚合操作的邻接矩阵供电时，出现了权重偏差问题。当k-hop邻域上有很多强连接时，边缘权重会呈指数级增长。如图3（左）和（右上）所示，有大量成员的组1之间有强连接。尽管参考组应该同时考虑组1和组2的实际情况，但权重只偏向于组1中的成员。
在(Liu et al. 2020)中，提出了一个非加权稀疏图的分解多尺度聚合，使用最短距离的概念，将一个邻接矩阵进一步泛化。然而，这并不适合行人轨迹预测，因为行人图是一个完整的图（Mohamed等人，2020），所有的行人节点只连接1跳（ ）。
分解行人之间的互动
我们提出了一种新颖的加权图上的社会关系的多尺度聚合。为了做到这一点，我们首先制作了一组图，其边缘由行人之间的距离尺度加权。我们根据 距离尺度k定义邻接矩阵为

其中，我们将比例设定为 .
因此， 可以表示为一组未加权的子图。将多项式项 与拆分后的邻接矩阵替换 ，方程（3）可以重新表述为。

如图3（右下角）所示，如果行人之间的距离在 ，就会形成一个强大的联系，即使他们的位置很远。有了这种表示方法，分解后的多尺度聚合能够使远处和近处的行人的社会互动都能被学习。

此外，通过根据距离拆分邻居，过度平滑的问题也得到了缓解。所有边的聚合显然会导致大量的不相关信息，特别是在拥挤的场景中。相比之下，在子图上拆分一个节点，通过自适应地聚合与尺度范围有关的信息，避免了过度平滑的问题。

3.3 空间-时间图谱聚合

行人图的多关系GCN
在本文中，我们的贡献之一是将多关系图的概念应用于行人的轨迹预测。与之前的工作（Mohamed等人，2020）不同的是，我们只考虑行人之间的相对位移而构建了一个图，我们同时使用欧氏距离和他们的相对位移。我们观察到，当一个模型只考虑距离或相对位移时，它就会避开同伴或走在后面的人而受到影响。
因此，我们的模型要协调学习互补的特征，以结合距离和相对位移信息。我们引入一个多关系图，其中有两类关系 ={（距离）；（相对位移）}。作为多关系图和分解的多尺度聚合的统一公式，我们推导出我们的模型如下。

其中，R是关系的数量，在这项工作中设置为2，因为我们同时考虑距离和相对位移边。 是一个归一化的邻接矩阵，其 程度矩阵为 。 每个关系的 尺度集是根据经验确定的，详细情况将在第4.2节描述。
空间-时间的行人图。
我们用一组空间图 描述了空间部分的聚集方法。正如(Mohamed et al. 2020)所建议的，我们另外进行连接，以定义行人节点之间的时间边缘，因为 对于所有 ，其中λ是一个用户定义的参数，用于控制邻居的数量。我们通过将它们沿着通道轴通过一个带有3×1滤波器的二维卷积层来实现。我们注意到，时间边缘图是在特征图的通道轴上堆叠的，以便在卷积操作之前代表时间。

3.4 加权图上的DropEdge

由于行人轨迹预测的数据集有限，最先进的模型往往存在过拟合问题。作为这个问题的解决方案，我们利用DropEdge技术（Rong等人，2020年），在训练阶段创建一个子图来随机移除输入图中的边缘。作为一个消息传递减速器和数据增强器，DropEdge减轻了基于非加权图的GCN的过拟合问题。

为了将DropEdge应用于我们基于加权图的多关系GCN，我们通过二进制矩阵与输入邻接矩阵的元素相乘来修改它。为了做到这一点，我们重新定义了关系邻接矩阵 ，它是 方程（2）中的一个归一化项，即：。

其中， 是原始节点上的随机连接边 是丢弃率， 代表元素相乘。我们将在第4.2节展示DropEdge对我们模型的有效性。

3.5 轨迹预测的全球时间聚合

时间预测CNN
利用第3.3节中的多关系GCN之后的时空特征，我们用我们设计的时间预测CNN（TPCNN）模块预测进一步的轨迹，而不是早期工作中常用的RNN（Alahi等人，2016；Gupta等人，2018）。我们的TPCNN模块包括两个TCN（Bai, Kolter, and Koltun 2018）作为推理模块和一个全局时间聚合作为细化模块，这将在接下来描述。TPCNN模块通过直接将卷积算子与时间通道一起应用于时空特征， 预测未来的时间特征 以正确推断进一步的轨迹。
全局性的时间合
大多数行人轨迹预测模型都有一个共同的问题，即随着序列变长，预测误差会累积。特别是，当一个人绕过障碍物或另一个人时，这个问题就会出现。在这项工作中，我们通过提出一个新颖的全局时间聚合（GTA）来解决这个问题，它可以学习补偿累积的误差。GTA将每个行人的轨迹作为输入，并输出一个单一的特征向量，加入到初始预测中。
对于时间段 ，GTA特征更新规则被定义为：。

其中h是时空特征H的一个元素。w和b分别表示可学习的内核权重和偏差。如图2（蓝框）所示，单一特征向量被添加到 每个行人的隐藏特征中，以最小化初始预测和实际路径之间的剩余误差。

3.6 实施细节

损失函数
和以前的工作一样（Xu, Yang, and Du 2020; Mohamed et al. 2020; Shi et al. 2020），我们使用双变量高斯概率密度函数。我们的模型预测行人n在时间t的 位置坐标的输出，其中是 一个多变量正态分布。 是x；y轴运动中的两个平均变量， 是相应的标准偏差， 是运动之间的相关系数 。使用预测的输出，我们最小化损失函数 ，如下所示。

其中分别 为x、y轴运动的地面实测坐标。
培训程序
我们构建了一个由GCN和TPCNN组成的统一模型，用于预测行人的运动轨迹。我们使用一个GCN和四个TPCNN块，这在消融研究中显示了最好的结果。我们的模型用SGD优化器训练了256个历时。我们使用128个小批量，初始学习率为1e - 4，每32个历时的衰减率为0：8。利用了随机旋转、翻转和缩放等数据增强方案。训练是在NVIDIA 2080Ti GPU上进行的，通常需要12小时。

---

5.结论

在本文中，我们提出了一种用于行人轨迹预测的新型DMRGCN架构。我们引入了一个多关系图来学习各种类型的社会互动，并提出了一个新颖的分解多尺度聚合，用一组子图来表示复杂的社会互动。此外，通过纳入时间卷积网络和我们新颖的全局时间聚合，我们能够纠正由过度回避导致的错误。我们的DMRGCN在公共数据集上的表现超过了最先进的方法。
存在改进DMRGCN的方向。一个是将类似于RNN模型的先验状态信息整合到TCN中，以实现更平滑的路径预测。另一个是将先验知识强加到场景配置和几何上。最后，DMRGCN假定摄像机是静态的。通过设计动态图模型来解除这一限制是未来自主车辆应用的一个重要挑战。