1.特征处理
1.标准化处理
from sklearn.preprocessing import StandardScaler
from sklearn.datasets import load_iris
iris = load_iris()
std = StandardScaler()
c = std.fit_transform(iris.data)
c

2.归一化
from sklearn.preprocessing import Normalizer
Normalizer().fit_transform(iris.data)

3.缩放法
from sklearn.preprocessing import MinMaxScaler
MinMaxScaler(feature_range=(1,2)).fit_transform(iris.data)
- 归一化和标准化应用场景
- 1.如果对输出结果范围有要求,则用归一化
- 2.如果数据较为稳定,不存在极端的最大值或最小值,则用归一化
- 3.如果数据存在异常值和较多噪声,则用标准化,这样可以通过中心化间接避免异常值和极端值的影响
- 4.支持向量机(SVM)、K近邻(KNN)、主成分分析(PCA)等模型必须使用归一化或标准化
4.定量特征二值化
from sklearn.preprocessing import Binarizer
- 阈值为3,所有大于3的数为1,所有小于等于3的数为0
Binarizer(threshold=3).fit_transform(iris.data)
5.定性特征编码(One-Hot)
- 例:假如变量为工人、学生、农民,及工人为(0,0,1),学生为(0,1,0),农民为(1,0,0)即为One-Hot编码
pd.get_dummies(iris.target, sparse=True)
from sklearn.preprocessing import OneHotEncoder
c = OneHotEncoder(categories='auto').fit_transform(iris.target.reshape((-1,1)))
c
>> <150x3 sparse matrix of type 'numpy.float64'>'
with 150 stored elements in Compressed Sparse Row format>
c.toarray()

6.缺失值处理
- strategy的参数
mean 平均值
median 中位数
most_frequent 众数
from sklearn.impute import SimpleImputer
d = SimpleImputer(strategy='mean').fit_transform(c)
d
- 2.pandas处理缺失值
- 删除缺失值
- how 为all 所有值为空才删除,默认any,有空值就删除
- inplace 在原数据上删除
- axis = 0 行 axis=1列
a.dropna(how='all',axis=0,inplace =True)
- 填充缺失值
- 使用前面的有效值向后填充,用ffill
- 使用后面的有效值向前填充用bfill
- axis =1,method=‘ffill’ 前一行的数据向后填充
a.fillna(method='ffill',axis=1)
a.fillna(np.mean(a.iloc[:,1]))
a.fillna(2)
7.重复值处理
- keep:接收特定 string,first 表示删除重复项并保留第一次出现的项;last 表示除了最后一项外,删除重复项;False 表示删除所有重复项;默认为 first;
- subset:接收 string 或 sequence,仅考虑用于标识重复项的某些列,默认情况下使用所有列,默认值为 None,只选择该列有重复的
b = a.duplicated(keep='first',subset=['nihao'])
b

- 删除nihao该列除第一行的所有重复行 默认为first
c = a.drop_duplicates(keep='first',subset=['nihao'])
c
8.异常值处理
- 1.正态分布删除异常值
- 数据要服从正态分布,使用3σ原则,异常值如超过3倍标准差,那么可以将其视为异常值,如果数据不服从正态分布,用远离平均值的多少倍标准差来描述。
from scipy import stats
mean = a['age'].mean()
std = a['age'].std()
print(stats.kstest(a['age'],'norm',(mean,std)))
>> KstestResult(statistic=0.19419645496061633, pvalue=0.058218287631895405)
data = a[np.abs(a['age']- mean) <= 3*std]
- 2.箱线图删除异常值
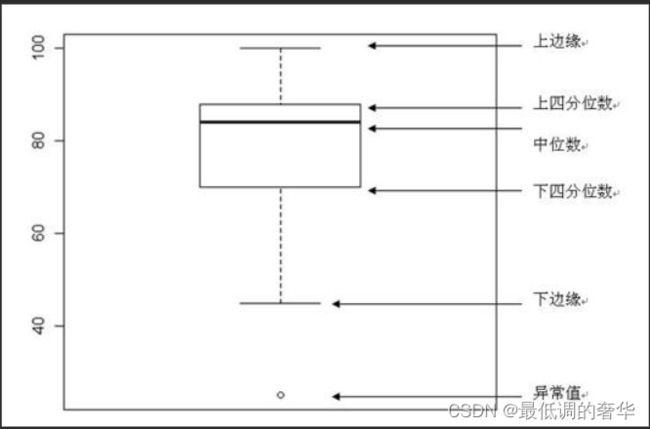
a['age'].plot(kind = 'box')
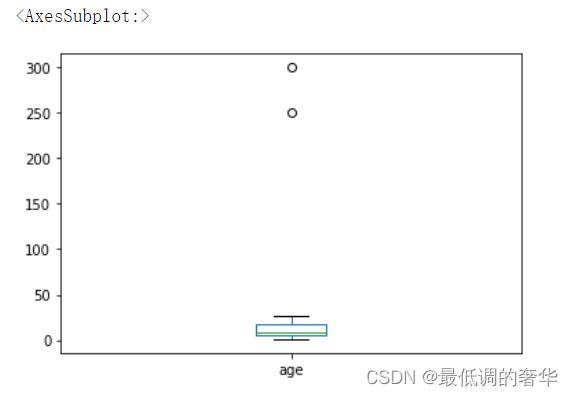
- 四分位距(IQR)就是上四分位与下四分位的差值。而我们通过IQR的1.5倍为标准,规定:超过(上四分位+1.5倍IQR距离,或者下四分位-1.5倍IQR距离)的点为异常值
>> 求下四分位数
q1 = a["age"].quantile(0.25)
q1
>> 求上四分位数
q3 = a["age"].quantile(0.75)
q3
iqr = q3 - q1
>> 下界
bottom = q1 - 1.5*iqr
bottom
>> 上界
upper = q3 + 1.5*iqr
upper
a[(a['age'] >= bottom) & (a['age'] <= upper)]
9.数据转换
np.log(a)
from sklearn.preprocessing import FunctionTransformer
a = np.arange(0,12).reshape(2,6)
a
>>array([[ 0, 1, 2, 3, 4, 5],
[ 6, 7, 8, 9, 10, 11]])
m = FunctionTransformer(np.log).fit_transform(a)
m
>>array([[ -inf, 0. , 0.69314718, 1.09861229, 1.38629436,
1.60943791],
[1.79175947, 1.94591015, 2.07944154, 2.19722458, 2.30258509,
2.39789527]])
2.特征选择
1.删除低方差特征
from sklearn.feature_selection import VarianceThreshold
b = VarianceThreshold(threshold=2).fit_transform(a)
b
X = X.drop(X.columns[X.std()==0], axis=1)
2.SelectKBest()方法
- f_classif,即利用ANOVA方法(方差分析(Analysis of Variance)又称F检验)来给特征打分,除此之外还有mutual_info_classif(基于互信息)、chi2(卡方检验)的方法来给特征打分后进行特征选择,这三种就可以用于常用的过滤法。
- 还有f_regression,mutual_info_regression则可以用于回归问题。
- 剩下的还有SelectPercentile (基于最高得分的百分位)等,可以根据以上举例选择需要的函数或者放入自己写的函数
from sklearn.feature_selection import SelectKBest,chi2,f_classif
SelectKBest(k=2).fit_transform(iris.data,iris.target)
c = SelectKBest(chi2,k=2)
d = c.fit_transform(iris.data,iris.target)
d
c.scores_
>>array([ 10.81782088, 3.7107283 , 116.31261309, 67.0483602 ])
c.pvalues_
>> array([4.47651499e-03, 1.56395980e-01, 5.53397228e-26, 2.75824965e-15])
- argsort()将索引从小到大排序,以下是将得分索引从大到小排序
m = np.argsort(c.scores_)[::-1]
m
e = pd.DataFrame(iris.data)
e
list(e.columns.values[m[0:2]])
>> 索引名称为 [2, 3]
from sklearn.feature_selection import SelectKBest,chi2,f_classif
import pandas as pd
import numpy as np
from sklearn.datasets import load_iris
iris = load_iris()
c = SelectKBest(chi2,k=2)
d = c.fit_transform(iris.data,iris.target)
m = np.argsort(c.scores_)[::-1]
e = pd.DataFrame(iris.data)
list(e.columns.values[m[0:2]])
3.主成分分析法(PCA)
- 主要原理是某种线性投影,将高维的数据映射到低维的空间表示,并期望在所投影的维度上的数据的方差最大,以此来达到使用较少的数据维度来保留较多的原数据点的效果
from sklearn.decomposition import PCA
- 1.整数 减少到特征数量
2.小数 0-1 90% 90%-95% 剩下百分之多少的数量:3个特征的95%就剩下2个特征
def pca():
"""
主成分分析进行特征选择
:return:
"""
pca = PCA(n_components=0.95)
data = pca.fit_transform(iris.data)
print(data)

4.线性判别分析法(LDA)
- 是一种有监督的线性降维算法,使降维后的数据点更容易较区分,利用了标签的特性
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis as LDA
LDA(n_components=2).fit_transform(iris.data,iris.target)








