论文翻译 - 深度学习社区发现综述 A Comprehensive Survey on Community Detection with Deep Learning
为大家介绍一篇「深度学习」在社区发现(图聚类/图划分)方面应用的最新综述论文。

作者:Xing Su
原文链接:https://arxiv.org/abs/2105.12584
Github链接:https://github.com/FanzhenLiu/Awesome-Deep-Community-Detection
文章目录
- 摘要
- 1 引言
- 2 相关符号与定义
- 3 社区发现的发展
- 4 深度学习社区发现的分类框架
- 5 基于卷积网络的社区发现
-
- 5.1 基于CNN的社区发现
- 5.2 基于GCN的社区发现
- 6 基于图注意力网络GAT的社区发现
- 7 基于生成对抗网络GAN的社区发现
- 8 基于自编码器AE的社区发现
-
- 8.1 基于堆叠自编码器的社区发现
- 8.2 基于稀疏自编码器的社区发现
- 8.3 基于降噪自编码器的社区发现
- 8.4 基于卷积自编码器的社区发现
- 8.5 基于图注意力自编码器的社区发现
- 8.6 基于变分自编码器的社区发现
- 9 基于深度非负矩阵分解的社区发现
- 10 基于稀疏滤波的社区发现
- 11 公开资源
-
- 11.1 数据集
-
- 现实世界数据集
- 人工合成数据集
- 11.2 评价指标
- 12 实际应用
- 13 未来方向
-
- 13.1 未知的社区数量
- 13.2 社区嵌入
- 13.3 层次化网络
- 13.4 多层网络
- 13.5 异构网络
- 13.6 网络异质性
- 13.7 拓扑不完备的网络
- 13.8 跨域网络
- 13.9 多属性视图网络
- 13.10 带符号的网络
- 13.11 动态网络
- 13.12 大规模网络
- 总结
摘要
社区揭示了其成员不同于网络中其他社区成员的特征和联系。在网络分析中,社区发现具有重要意义。除了经典的谱聚类和统计推断方法,凭借处理高维网络数据方面的优势, 用于社区发现的深度学习技术近年来有了显著的发展。因此,对于学术界和从业者而言,对深度学习应用于社区发现的最新进展进行及时地总结和梳理是具有重要意义的。针对基于深度学习的社区发现技术的最新进展,本文提出了一种新的分类框架,包括基于深度神经网络的深度学习模型、深度非负矩阵分解和深度稀疏滤波,并进一步将深度神经网络模型细分为卷积网络,图注意网络,生成对抗网络和自编码器。在实验设置方面,本文总结了流行的对比基准数据集、模型评估指标和开源实现项目。不仅讨论了社区发现在各个领域的实际应用,还提出了实现方案。文章在最后提出了快速发展的用于社区发现的深度学习领域中具有挑战性的课题,并概述了该领域未来的发展方向。
1 引言
早在上世纪 20 年代,社会学领域的科学家们就对「社区」展开了研究[1]。然而,直到 21 世纪,研究者们才真正开始借助强大的数学工具和大数据处理技术来解决社区发现任务中的难题[2]。自2002年Girvan和Newman的研究使这一图分割问题受到广泛关注以来[3],计算机科学家们在过去的 10 年间通过利用网络拓扑结构[5-8]和实体语义信息[9-11],对不同规模大小的静态、动态网络[12-17]中的社区发现问题[4]展开了广泛研究。越来越多的基于图的方法被提出,用于在具有复杂数据结构的环境中进行社区发现[18][19]。通过社区发现,我们可以详细分析社区在网络中的演化和影响(例如,谣言传播、病毒爆发、肿瘤演化)。
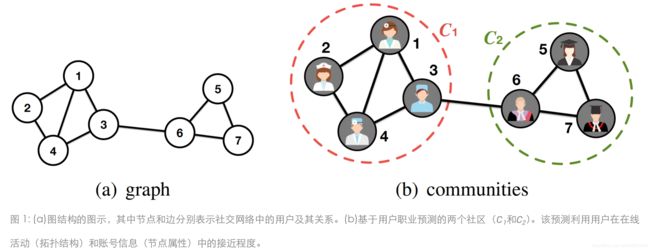
社区的存在使得社区发现技术的意义逐渐得以凸显。正所谓“物以类聚,人以群分”[20]。根据六度分隔理论,最多通过六个人就能够认识任何一个陌生人[21]。因此,我们所处的世界是一个由一系列社区形成的巨大网络。如图 1 所示,通过发现社交网络中的社区[22-24],平台运营者可以向目标用户推荐商品。而在引文网络中[25],社区发现可以检测出研究课题的重要性、关联性和演化情况,并确定研究的发展趋势。在代谢网络[26][27]和蛋白质相互作用 (PPI)网络[28]中,社区发现可以揭示具有类似生物学功能的代谢物和蛋白质。同样地,脑网络[19][29]中的社区可以反映出不同功能的脑区域。
对于一些小型的网络和简单的场景,研究人员已经提出了一系列基于谱聚类[30][31]、统计推断[32-35]等传统技术的社区发现方法。然而,由于计算及存储空间成本巨大,这类方法并没有扩展到大型网络或具有高维特征的网络上。在现实世界的网络中,大量的非线性结构信息使传统的模型并不能够很好地应用于实际场景。因此,我们需要发展出具有良好计算性能的更强大的技术。如今,针对这一问题,深度学习从以下3个方面给出了最为灵活的解决方案:(1)学习非线性网络属性,如节点之间的关系;(2)提供能够保留复杂网络结构特征的低维网络表示;(3)利用更多信息进行社区发现以提高性能。总而言之,深度学习用于社区发现是一种新的趋势,我们需要一个及时全面的综述。
据我们所知,本文是第一篇综合概述深度学习对社区发现贡献的综述研究。现有的综述大都聚焦于传统方法,归纳其对发现网络固有模式和功能的重要影响[36][37]。在现有的社区发现综述中,有学者对各类不同的技术进行综述,如SBMs[38],LPAs[39][40],多目标或单目标优化算法等[13][14]。也有学者从网络的角度,分别对动态网络[12]、有向网络[41]、多层网络[5]中的社区发现方法进行综述。此外,还有针对非重叠或重叠社区发现的综述[6][7]。就应用场景而言,也有专门针对社交网络的社区发现综述[9][42]。
本文旨在从以下方面帮助研究人员和从业者了解社区发现领域的过去、现在和未来的趋势:
- 系统的分类和深入的调研。我们对基于深度学习的社区发现方法提出了一个新的分类框架(见图3),并分析、总结、比较了每一类别的代表性工作。同时,介绍了社区发现在现实世界的实际应用。为未来的方向与发展提供了新视角。
- 丰富的资源和高影响力的参考文献。本文不仅概述方法,还整合了社区发现的基准数据集、评估指标、开源实现和实际应用的资源。我们广泛概述了高影响力国际会议和高质量期刊上发表的相关研究,涵盖了人工智能、机器学习、数据挖掘几大领域。
- 未来的发展方向。由于将深度学习应用于社区发现是一个新的研究趋势,我们讨论了当前研究的局限性,以 及未来研究的关键挑战和开放性问题。
2 相关符号与定义
本章节的主要内容包括相关定义和符号的含义,以及深度学习社区发现模型的输入和输出。
- 定义1(网络): 一个网络可表示为 G = ( V , E ) \mathcal{G}=(V, E) G=(V,E),其中 V V V是节点集合, E E E是边集。 v i ∈ V v_{i} \in V vi∈V表示一个节点, e i j = ( v i , v j ) ∈ E e_{ij}=(v_{i}, v_{j}) \in E eij=(vi,vj)∈E表示节点 v i v_{i} vi和 v j v_{j} vj之间存在一条边。一个节点 v i v_{i} vi的邻域则为 N ( v i ) = { u ∈ V ∣ ( v i , u ) ∈ E } N(v_i)=\{u\in V|(v_i, u)\in E\} N(vi)={u∈V∣(vi,u)∈E}。 邻接矩阵 A = [ a i j ] A=[a_{ij}] A=[aij]是一个 n × n n \times n n×n维的矩阵,如果 e i j ∈ E e_{ij}\in E eij∈E,则 a i j = 1 a_{ij}=1 aij=1;如果 e i j ∉ E e_{ij}\notin E eij∈/E,则 a i j = 0 a_{ij}=0 aij=0。如果 a i j ≠ a j i a_{ij}\neq a_{ji} aij=aji, G \mathcal{G} G为有向网络,否则为无向网络。如果 a i j a_{ij} aij存在权值 w i j ∈ W w_{ij}\in W wij∈W, G = ( V , E , W ) \mathcal{G}=(V, E, W) G=(V,E,W)为带权网络,否则为无权网络。如果 a i j a_{ij} aij有不同的值 + 1 , − 1 +1, -1 +1,−1, G \mathcal{G} G为带正边和负边的符号网络。如果节点 V V V有属性 X = { x i } 1 n X=\{x_i\}_1^n X={xi}1n, G = ( V , E , X ) \mathcal{G}=(V, E, X) G=(V,E,X)为属性网络,其中 x i ⊆ R d x_i\subseteq \mathbb{R}^d xi⊆Rd表示节点 v i v_i vi的属性向量,否则 G \mathcal{G} G为无属性网络。当网络随时间 t t t演化时,即为动态网络 G ( t ) = ( V t , E t ) \mathcal{G}_{(t)}=(V_{t}, E_{t}) G(t)=(Vt,Et)或时态网络 G ( t ) = ( V , E , X t ) \mathcal{G}_{(t)}=(V, E, X_{t}) G(t)=(V,E,Xt)。
- 定义2(社区): 社区的集合为 C = { C 1 , C 2 , ⋯ , C k } \mathcal{C}=\{C_1, C_2, \cdots, C_k\} C={C1,C2,⋯,Ck},每个社区 C i C_i Ci是网络 G \mathcal{G} G的划分,该划分保留了网络的区域结构和簇属性。社区 C i C_i Ci中的节点 v i v_i vi应满足其社区内部度大于外部度。如果 C i ∩ C j = ∅ C_i \cap C_j = \emptyset Ci∩Cj=∅, ( ∀ i , j \forall i, j ∀i,j),那么 C \mathcal{C} C是非重叠社区;否则,它是节点可以同时隶属于多个社区的重叠社区。
| 符号 | 含义 | 符号 | 含义 | 符号 | 含义 |
|---|---|---|---|---|---|
| R \mathbb{R} R | 数据空间 | G \mathcal{G} G | 图 | V V V | 节点集合 |
| E E E | 边集合 | C \mathcal{C} C | 社区集合 | v i v_i vi | 节点 v i ∈ V v_i \in V vi∈V |
| e i j e_{ij} eij | 边 e i j ∈ E e_{ij} \in E eij∈E | C k C_k Ck | 第 k k k个社区 | N ( i ) N(i) N(i) | 节点 v i v_i vi的邻居 |
| n n n | 节点数量 n = ∣ V ∣ n = \mid V \mid n=∣V∣ | m m m | 边数 m = ∣ E ∣ m = \mid E \mid m=∣E∣ | A A A | 邻接矩阵 |
| A ( + , − ) A(+,-) A(+,−) | 符号网络邻接矩阵 | A i j \mathcal{A_{ij}} Aij | 图 ( G i , G j ) (\mathcal{G_{i}}, \mathcal{G_{j}}) (Gi,Gj) 之间的锚链接 | X \mathcal{X} X | 异构网络节点属性 |
| X X X | 节点属性矩阵 | x i x_i xi | 节点 v i v_i vi的属性向量 | y i y_i yi | 节点 v i v_i vi的标签 |
| y i k y_i^k yik | 节点 v i v_i vi属于 C k C_k Ck的二元社区标签 | c k c_k ck | 社区 C k C_k Ck的标签 | d d d | 属性 x i x_i xi的维度 |
| D D D | 度矩阵 | L L L | 拉普拉斯矩阵 | l l l | DNN第 l l l层 |
| W ( l ) W^{(l)} W(l) | 第 l l l层权重矩阵 | σ ( ⋅ ) \sigma(\cdot) σ(⋅) | 激活函数 | H ( l ) H^{(l)} H(l) | 第 l l l层激活矩阵 |
| h i ( l ) h_{i}^{(l)} hi(l) | 节点 v i v_i vi在第 l l l层的表示向量 | Z Z Z | 特征 | z i z_i zi | 节点 v i v_i vi对特征向量 |
| B B B | 模块度矩阵 | b i j b_{ij} bij | 节点 ( v i , v j ) (v_i, v_j) (vi,vj)之间的模块度值 | Q Q Q | 模块度评价指标 |
| M M M | 马尔科夫矩阵 | S S S | 相似度矩阵 | s i j s_{ij} sij | 节点 ( v i , v j ) (v_i, v_j) (vi,vj)之间的相似度值 |
| O O O | 社区隶属度矩阵 | o i j o_{ij} oij | 节点 ( v i , v j ) (v_i, v_j) (vi,vj)之间的社区隶属度值 | U / P U/P U/P | 非负矩阵 |
| p i j p_{ij} pij | 社区隶属概率 ( v i , C j ) (v_i, C_j) (vi,Cj) | L \mathcal{L} L | 损失函数 | Ω \Omega Ω | 稀疏惩罚 |
| ∣ ⋅ ∣ \vert \cdot \vert ∣⋅∣ | 集合大小 | ∣ ∣ ⋅ ∣ ∣ \vert\vert \cdot \vert\vert ∣∣⋅∣∣ | 范数运算符 | Θ \Theta Θ | 可训练参数 |
| P r ( ⋅ ) Pr(\cdot) Pr(⋅) | 概率分布 | ϕ g \phi_g ϕg | 生成器 | ϕ d \phi_d ϕd | 判别器 |
| ϕ e \phi_e ϕe | 编码器 | ϕ r \phi_r ϕr | 解码器 |
- 社区发现输入 基于深度学习的社区发现模型将网络结构和其它属性信息作为输入,如节点属性和带符号的边。网络结构是以节点和边代表的拓扑关系。边上的权重代表连接强度。节点属性代表节点的语义信息,例如在线社交网络中用户的账号信息。带符号的边代表连接状态,如正连接(+)和负连接(-)。
- 社区发现输出 社区发现模型的输出通常是一些将节点和边分组后的社区,这些社区可以是重叠或非重叠的。如图2所示,这些社区可能不相交也可能相交,本文对这两类社区都进行了概述。
3 社区发现的发展
社区发现在网络分析和数据挖掘领域具有重要意义,图4展示了传统方法和基于深度学习方法的发展。传统方法在网络结构上进行社区发现,它们可以分为7类(如图3左)且只能发现浅层关联,因此结果往往是次优的,本章简单回顾了其中的代表性工作。而基于深度学习的社区发现方法(如图3右)可以发现深层的网络信息和复杂的关系、处理高维数据。
图划分:此类方法也被称为图聚类[36],它将网络划分为 k 个社区。聚类簇中的边要比聚类簇之间的边更为稠密。代表性的算法包括:Kernighan-Lin 启发式方法[43]、谱二分法[44]等。此类方法在深度学习方法中仍然被使用。
统计推断:代表性的算法为随机块模型(SBM)[32],这是一类被广泛使用的生成式模型,它将节点分配到社区中,并控制它们的似然概率。其变体包括:DCSBM[33]、MMB[34]、OSBM[35] 等。
层次聚类:此类方法通过分裂式、凝聚式和混合式三种方式发现不同层次上的社区结构。Girvan-Newman(GN)算法通过分裂式方法依次删除网络中的边从而发现新的社区,输出一种关于社区结构的层次化树状表征[2][45]。FastQ [3][46]是一种凝聚式算法,它逐渐将节点合并为一个社区。CDASS 算法[47]同时应用了分裂式和凝聚式策略,基于结构相似度对图进行划分,并将其合并为层次化的社区。
动力学方法:随机游走利用随机游走器在一段较短的游走中陷入某个社区的趋势,是最常被用于社区发现任务的动力学方法。代表性的算法包括:WalkTrap[48]、InfoMap[49]、LPA[50]、LPAm[51]。
谱聚类:网络的谱属性可以被用于社区发现任务。谱聚类[30]基于邻接矩阵派生的网络归一化拉普拉斯矩阵划分节点,并且使用伪似然算法将划分结果拟合到 SBM 算法上。
基于密度的方法:此类方法的代表性算法包括:DBSCAN[52]、SCAN[53]、LCCD[54]。它们通过测量实体密度来确定社区、社区边界和异常。
优化方法:社区发现方法利用优化算法来达到某个极值,通常期望表明社区的似然。最经典的优化函数为 Modularity(Q) [45]及其变体FastQ[3][46],它被用来估计网络划分得到的社区结构,公式如下[37]:
Q = 1 2 m ∑ i j ( a i j − p i j ) δ ( C i , C j ) , Q = \frac{1}{2m}\sum_{ij}(a_{ij} - p_{ij})\delta(C_i, C_j), Q=2m1ij∑(aij−pij)δ(Ci,Cj),
其中, C i C_i Ci和 C j C_j Cj是节点 v i v_i vi和 v j v_j vj所属的社区, δ \delta δ是克罗内克增量函数,当 C i = C j C_i=C_j Ci=Cj时为1,否则为0。 P = [ p i j ] P=[p_{ij}] P=[pij]是原始网络随机集合的平均邻接矩阵。 P P P 保留了网络特征,例如二分性、相关性、带符号边和空间嵌入性。标准的 P P P为 p i j = k i k j / 2 m p_{ij}=k_ik_j/2m pij=kikj/2m[45],其中 k i k_i ki和 k j k_j kj为节点度。Louvain [56]是另一种著名的优化算法,它采用节点移动策略提取具有更大网络模块度的社区结构。此外,贪婪优化方法还包括模拟退火[57]、极值优化[58]、以及谱优化[59]。演化社区发现方法在局部学习和全局搜索中十分有效[60],它分为单目标优化和多目标优化。多智能体遗传算法(MAGA-Net)[61]等单目标优化算法利用了模块度函数,而 Combo[62]等算法则融合了归一化互信息(NMI)[63]、Conductance[64]在内的多个优化目标。CE-MOEA [10]算法基于非支配排序遗传算法(NSGA-II)[65]来优化模块度和相似性目标。
为什么需要深度学习进行社区发现? 特别是在大型复杂网络中,深度学习模型 [66] 具有利用节点、邻域、边、子图等的高维非线性特征(即网络拓扑信息)和高维关系特征(即网络属性信息)的优势。 这样的模型对稀疏网络更具弹性,并且更适合现实世界场景中的无监督学习任务。
4 深度学习社区发现的分类框架
本文提出了一个针对基于深度学习的社区发现方法的分类框架。该框架将相关方法总结为六类:卷积网络、图注意力网络 (GAT)、生成对抗网络 (GAN)、自编码器 (AE)、深度非负矩阵分解 (DNMF) 和深度稀疏过滤 (DSF)。卷积网络包括卷积神经网络(CNN)和图卷积网络(GCN)。AE 进一步分为堆叠 AE、稀疏 AE、去噪 AE、图卷积 AE、图注意力 AE 和变分 AE (VAE) 等子类别。 分类结构如图 3 所示。代表性工作的时间线如图 4 所示。
5 基于卷积网络的社区发现
卷积神经网络(CNN)[67]是一种针对网格式拓扑数据,如图像数据,而提出的前馈深度神经网络(DNN),其中卷积层降低了计算成本,而池化操作保证了 CNN 在特征表达上的鲁棒性。图卷积网络(GCN)[68]是基于CNN 和图的局部谱滤波器的一阶近似而提出的用于图结构数据的卷积网络模型。GCN中使用的传播规则设计为:
H ( l + 1 ) = σ ( D ~ − 1 2 A ~ D ~ − 1 2 H ( l ) W ( l ) ) , H^{(l+1)} = \sigma (\tilde{D}^{-\frac{1}{2}} \tilde{A} \tilde{D}^{-\frac{1}{2}} H^{(l)}W^{(l)} ), H(l+1)=σ(D~−21A~D~−21H(l)W(l)),其中, H ( l ) H^{(l)} H(l)通过激活函数 σ ( ⋅ ) \sigma(\cdot) σ(⋅)和层特定的可训练权重矩阵 W l W^{l} Wl保留第 l l l 层中的潜在表示矩阵 ( H ( 0 ) = X ) (H^{(0)}=X) (H(0)=X); A ~ = A + I n \tilde{A}=A+I_n A~=A+In为无向图 G \mathcal{G} G加入自连接后的邻接矩阵, I n I_n In是单位矩阵; D ~ i i = ∑ j a ~ i j \tilde{D}_{ii}=\sum_j\tilde{a}_{ij} D~ii=∑ja~ij,其中 a ~ i j ∈ A ~ \tilde{a}_{ij}\in\tilde{A} a~ij∈A~。
5.1 基于CNN的社区发现
现有的基于CNN的社区发现方法具有严格的数据输入限制:图像格式数据和带标签数据。 因此,这些方法需要对其输入进行预处理:(1)将网络样本映射为图像数据格式,以及(2)提前手动标记节点或社区,因为大多数现实世界的网络没有标签。 图 5 展示了基于 CNN 的社区发现方法的通用框架。 为了解决社区发现中的特定问题,现有的研究开发了以下一系列技术。
传统的社区发现技术以完整的网络拓扑结构为前提,发现过程依赖于测量邻域内节点相似性的图分析。 然而,现实世界中的网络获得的结构信息有限,不完整的网络会影响邻域分析并进一步降低社区发现的准确性。CNN 架构可以从基本输入中逐渐恢复完整的潜在特征,于是一个针对拓扑不完备网络 (TINs)的有监督CNN 模型 [8] 被提出以进行社区发现。该模型有两个 CNN 层,分别是用于网络表示的最大池化算子和用于社区发现的全连接 DNN 层。卷积层从不同的角度表示每个节点的局部特征, 最后的全连接层 f f f更新每个节点 v i v_i vi的社区:
o i k = σ ( b k f + W k f h i ( 2 ) ) , o_i^k = \sigma(b_k^f + W_k^f\bm{h}^{(2)}_i), oik=σ(bkf+Wkfhi(2)), 其中, σ \sigma σ是sigmoid函数, W f k W_f^k Wfk和 b k f b^f_k bkf是第 k k k个神经元 o i k o^k_i oik的权重和偏置, h i ( 2 ) h^{(2)}_i hi(2)是前两个卷积层输出的节点表示向量。该模型执行反向传播以通过最小化损失函数 L \mathcal{L} L来进行优化:
L = 1 2 ∑ i ∥ o i − y i ∥ 2 2 = 1 2 ∑ i ∑ k ( o i k − y i k ) 2 , \mathcal{L} = \frac{1}{2}\sum_i\|\bm{o}_i - \bm{y}_i\|_2^2 = \frac{1}{2}\sum_i\sum_k(o_i^k - y^k_i)^2, L=21i∑∥oi−yi∥22=21i∑k∑(oik−yik)2, 其中 y i \bm{y}_i yi 表示真实标签向量, y i k ∈ { 0 , 1 } y_i^k\in\{0, 1\} yik∈{0,1} 表示节点 v i v_i vi 是否属于第 k k k 个社区。该模型在 TINs 中的社区发现实验的准确率约为80%,其中 10%的节点被标记,其余为未标记节点。这表明多跳范围内的高阶邻域表示可以提高社区发现的准确率。 为了处理大规模社交网络中的高稀疏性,[69]为TINs进一步设计了稀疏卷积矩阵。
ComNet-R (Community Network Local Modularity R) [70] 是一种用于社区发现的 edge-2-image 模型,用于对社区内和社区之间的边进行分类。ComNet-R先移除社区间的边,以形成的初始社区。然后通过局部模块度优化方法来合并获得最终社区。
5.2 基于GCN的社区发现
GCN在图卷积层中聚合节点的邻域信息,因此可以从全局上捕获用于社区发现的复杂特征。基于GCN的社区发现方法有两类:(1)监督/半监督社区分类;(2)基于无监督网络表示的社区聚类。社区分类方法受到现实世界中缺乏标签的限制,相比之下,通过矩阵重构和目标优化等技术,对网络表示进行聚类可以更灵活地发现社区结构。图 6 展示了GCN通常如何应用于社区发现,表 V(见原文附录)对比了这些技术。
GCN 采用一些传统的社区发现方法作为深度图算子,例如用于统计推断的随机块模型 (SBM)、用于谱分析的拉普拉斯矩阵和用于信念传播的概率图模型。 例如,LGNN (Line Graph Neural Network)[71] 是一种有监督的社区发现模型,它以更好的社区检测性能改进了 SBM,并降低了计算成本。LGNN将非回溯算子与信念传播的消息传递规则相结合 [72],学习有向网络中节点表示的特征。使用softmax函数识别节点 v i v_i vi 属于社区 C k C_k Ck ( o i , k = p ( y i = c k ∣ Θ , G o_{i,k} = p(y_i=c_k|\Theta,\mathcal{G} oi,k=p(yi=ck∣Θ,G) 的条件概率,并最小化社区标签所有可能排列 ( S C S_{\mathcal{C}} SC) 的交叉熵损失:
L ( Θ ) = min π ∈ S C − ∑ i log o i , π ( y i ) . \mathcal{L}(\Theta)=\min_{\pi \in S_{\mathcal{C}}}{-\sum_i\log{o_{i, \pi(y_{i})}}}. L(Θ)=π∈SCmin−i∑logoi,π(yi). 由于 GCN 最初不是为社区发现任务设计的,因此社区结构不是学习节点嵌入的重点,并且社区和节点之间的结构一致性没有平滑约束。为此,一种半监督 GCN 社区发现模型 (MRFasGCN) [11] 被提出来表征隐藏的社区。它将针对网络的马尔可夫随机场扩展为一个新的卷积层 (eMRF),使 MRFasGCN 面向社区并对 GCN 的粗略结果起到了平滑细化作用。
CommDGI (Community Deep Graph Infomax) [73] 通过节点和社区上的互信息 (MI) 联合优化图表示和聚类,并最大化图模块度。它将 k k k-means 应用于节点聚类并以聚类中心为目标。
在概率推理框架下,检测重叠社区的问题可以通过推断节点的社区从属关系的生成模型来解决。例如,NOCD (Neural Overlapping Community Detection) [74] 结合了伯努利-泊松 (BP) 概率模型和两层 GCN,通过最小化 BP 的负对数似然来学习社区从属向量。 通过设置阈值来不断识别和移除弱从属关系,从而获得最终社区结构。
谱GCN代表节点邻域的所有潜在特征。通过在深层 GCN 层中重复进行拉普拉斯平滑,相邻节点的特征将收敛到相同的值。然而,这些模型会导致社区发现的过度平滑问题。 为了减少这种负面影响,GCLN (Graph Convolutional Laddershape Networks) [75] 设计了一种基于CNN领域U-Net的新型GCN架构用于无监督社区检测( k k k-means)。GCLN对称地构建了收缩路径和扩展路径,将从收缩路径中捕获的上下文特征与在扩展路径中学到的本地化信息融合。
由于不同类型的连接通常被视为普通边,因此GCN单独表示每种类型的连接并将它们聚合会导致冗余表示。IPGDN (Independence Promoted Graph Disentangled Network) [76] 将邻域区分为不同部分,并自动发现图的独立潜在特征的细微差别,从而降低发现社区的难度。 IPGDN 由邻域路由中的希尔伯特-施密特独立准则 (HSIC) 正则化 [77] 支持。
对于属性图,基于GCN的社区发现依赖于结构信息和表征特征,其中相邻节点和具有相似特征的节点很可能聚集到同一个社区。因此,图卷积将上述两个图信号相乘,并且需要平滑滤除高频噪声。 为此,AGC (Adaptive Graph Convolution) [78] 设计了一个具有频率响应函数的低通图滤波器:
p ( λ q ) = ( 1 − 1 2 λ q ) k , p(\lambda_q) = (1 - \frac{1}{2} \lambda_q)^k, p(λq)=(1−21λq)k, 其中 G \mathcal{G} G的频率响应函数 p ( Λ ) = diag ( p ( λ 1 ) , ⋯ , p ( λ n ) ) p(\Lambda)=\text{diag}(p(\lambda_1),\cdots,p(\lambda_n)) p(Λ)=diag(p(λ1),⋯,p(λn))在落入区间 [ 0 , 2 ] [0, 2] [0,2]的对称归一化图拉普拉斯算子 L s L_s Ls的所有特征值 λ q \lambda_q λq上递减且非负。随着 k k k的增加, p ( λ q ) p(\lambda_q) p(λq)变得更加低通,表明过滤后的节点特征 X ˉ \bar{X} Xˉ将更加平滑。AGC选择合适的邻域跳跃大小 k k k,并通过 k k k阶图卷积将图特征表示为:
X ˉ = ( I − 1 2 L s ) k X , \bar{X} = (I - \frac{1}{2}L_s)^kX, Xˉ=(I−21Ls)kX, 再进行谱聚类。
AGE (Adaptive Graph Encoder) [79] 是另一种可扩展到社区发现的平滑滤波器相关的GCN模型。为了生成平滑特征,AGE 自适应地执行成对节点相似性 ( S = [ s i j ] S = [s_{ij}] S=[sij]) 和 t t t堆叠拉普拉斯平滑滤波器 ( X ˉ = ( I − γ L ) t X \bar{X} = (I - \gamma L)^t X Xˉ=(I−γL)tX):
L = ∑ ( v i , v j ) ∈ V ′ − y i j log ( s i j ) − ( 1 − y i j ) log ( 1 − s i j ) , \mathcal{L} = \sum_{(v_i,v_j)\in V'} -y_{ij}\log(s_{ij}) - (1-y_{ij})\log(1 - s_{ij}), L=(vi,vj)∈V′∑−yijlog(sij)−(1−yij)log(1−sij), 其中 V ′ V' V′表示正(相似)和负(不相似)样本上的平衡训练集, y i j y_{ij} yij是节点对 ( v i , v j ) (v_i,v_j) (vi,vj)上排序后的二元相似性标签。
一些工作对GCN过滤器具有重要贡献。例如,在谱图卷积架构中,基于Cayley多项式的GNN ——CayleyNets (Graph Convolutional Neural Networks with Cayley Polynomials) [80] 提出了一种有效的Cayley滤波器,用于社区发现的高阶近似。 它专门研究窄带滤波,因为低频包含了大量可用于社区发现的社区信息。CayleyNets 与 Cayley 过滤器结合,在谱卷积层中利用平均池化,并在节点上使用半监督 softmax 分类器,来对社区成员归属进行预测。
6 基于图注意力网络GAT的社区发现
基于图注意力网络(GAT)的社区发现方法可以发现复杂网络场景中的社区。如图 7 所示, GAT [81] 通过可训练的权重聚合邻域中节点的特征,该权重通过考虑多种因素(特别是具有多种关系类型的网络)的注意力来计算:
h i ( l + 1 ) = σ ( ∑ j ∈ N ( v i ) α i j ( l + 1 ) W ( l + 1 ) h j ( l ) ) , \bm{h}_i^{(l+1)}=\sigma\left(\sum_{j \in N(v_i)} \alpha_{i j}^{(l+1)} W^{(l+1)} \bm{h}_{j}^{(l)}\right), hi(l+1)=σ⎝⎛j∈N(vi)∑αij(l+1)W(l+1)hj(l)⎠⎞, 其中 h i l \bm{h}_{i}^l hil 表示第 l l l 层 ( h i ( 0 ) = x i \bm{h}_{i}^{(0)} = \bm{x}_i hi(0)=xi) 节点 v i v_i vi 的输出表示, α i j ( l ) \alpha_{i j}^{(l)} αij(l) 是 v i v_i vi 和 v j ∈ N ( v i ) v_j \in N(v_i) vj∈N(vi)之间的注意力系数。
深度社区发现模型需要特别注意网络中节点间的关系。例如,在将论文归类为研究主题时,合著关系和引用关系都很重要。多层网络提供具有多个网络层的 DNN 结构,以实现对多个图的交互的综合分析。DMGI (Deep Graph Infomax for Attributed Multiplex network embedding ) [82] 独立嵌入每种关系类型并通过最大化全局共享特征来计算网络嵌入用于发现社区,一种共识正则化被应用于注意力系数,以在嵌入中削弱不太重要的关系。
MAGNN (Metapath Aggregated Graph Neural Network) [83] 通过多信息语义元路径提供了一种卓越的社区发现解决方案,这些元路径区分了图注意力层中的异构结构。MAGNN 从语义信息生成节点属性。由于元路径内和元路径间存在异构节点和边,MAGNN 通过聚合节点和元路径上的语义差异,在它们的嵌入中利用了注意机制。因此,MAGNN 能够为社区发现提取更丰富的拓扑和语义信息。
7 基于生成对抗网络GAN的社区发现
对抗性训练在生成模型中是有效的,可以提高判别能力,但在应用于社区发现时需要解决过拟合问题(如图 8)。 生成对抗网络 (GAN) [84] 在对抗训练中,在生成器 ϕ g \phi_g ϕg 和判别器 ϕ d \phi_d ϕd 之间进行竞争。 ϕ d ( x ) \phi_d(\bm{x}) ϕd(x) 表示输入数据的概率,而 ϕ g ( z ) \phi_g(\bm{z}) ϕg(z) 学习生成器在输入噪声变量 p z ( z ) p_{\bm{z}}(\bm{z}) pz(z) 上的数据 x \bm{x} x 上的分布 p g p_g pg 。生成器通过生成假样本来欺骗鉴别器。其目标函数定义为:
min ϕ g max ϕ d E x ∼ p d a t a ( x ) [ log ϕ d ( x ) ] + E z ∼ p z ( z ) [ log ( 1 − ϕ d ( ϕ g ( z ) ) ) ] . \min_{\phi_g} \max_{\phi_d} \mathbb{E}_{\bm{x} \sim p_{data}(\bm{x})} [\log \phi_d(\bm{x})] + \mathbb{E}_{\bm{z} \sim p_{\bm{z} }(\bm{z} )} [\log (1-\phi_d(\phi_g(\bm{z} )))]. ϕgminϕdmaxEx∼pdata(x)[logϕd(x)]+Ez∼pz(z)[log(1−ϕd(ϕg(z)))].
SEAL (Seed Expansion with Generative Adversarial Learning) [85] 通过具有增量更新的图指针网络 (iGPN),从选定的种子节点中生成社区。它由社区层面的四个部分组成,即生成器、鉴别器、种子选择器和定位器。鉴别器采用图同构网络 (GIN) 来修改具有真实社区标签的生成社区。定位器旨在为生成器提供正则化信号,从而消除社区发现中的不相关节点。
对于不平衡社区,DR-GCN (Dual-Regularized Graph Convolutional Networks) [86]将条件 GAN 用于双正则化 GCN 模型,即潜在分布对齐正则化和类条件对抗正则化。第一个正则化通过在标准 GCN 训练 ( L g c n \mathcal{L}_{gcn} Lgcn) 的指导下最小化多数和少数社区类 ( L d i s t \mathcal{L}_{dist} Ldist) 之间的 Kullback-Leibler (KL) 差异来平衡社区: L = ( 1 − α ) L g c n + α L d i s t \mathcal{L}=(1-\alpha)\mathcal{L}_{gcn}+\alpha \mathcal{L}_{dist} L=(1−α)Lgcn+αLdist。 第二个正则化旨在区分标记节点表示上的社区:
min ϕ g , L max ϕ d L ( ϕ d , ϕ g ) = E x ∼ p d a t a ( x ) log ϕ d ( x ∣ y ) + E z ∼ p z ( z ) [ log ( 1 − ϕ d ( ϕ g ( z ∣ y ) ) ) + L r e g ] , \min_{\phi_{g}, \mathcal{L}} \max_{\phi_d} \mathcal{L}(\phi_d, \phi_g) = \mathbb{E}_{\bm{x} \sim p_{data}(\bm{x})} \log \phi_d(\bm{x} \mid y) + \mathbb{E}_{\bm{z} \sim p_{\bm{z}}(\bm{z})} [\log(1-\phi_d(\phi_g(\bm{z} \mid y))) + \mathcal{L}_{reg}], ϕg,LminϕdmaxL(ϕd,ϕg)=Ex∼pdata(x)logϕd(x∣y)+Ez∼pz(z)[log(1−ϕd(ϕg(z∣y)))+Lreg],其中 L r e g = ∑ v j ∈ N ( x ) ∥ h g x − h j ∥ 2 \mathcal{L}_{reg}=\sum_{v_j \in N(\bm{x})}\|\bm{h}_{g_{\bm{x}}}-\bm{h}_j\|_2 Lreg=∑vj∈N(x)∥hgx−hj∥2 强制生成的假节点 ( g x g_\bm{x} gx) 重建各自的邻域关系(如 v j ∼ x v_j\sim \bm{x} vj∼x)。
JANE (Jointly Adversarial Network Embedding) [87] 不是通过鉴别器仅生成一种假样本,而是采用拓扑和节点属性的两种网络信息来捕获来自真假样本对抗组的语义变化。 具体来说,JANE 通过多头自注意力编码器 ( ϕ e \phi_e ϕe) 表示社区特征,其中为假特征(来自 Z Z Z)添加高斯噪声,以与生成器 ( ϕ g \phi_g ϕg) 和鉴别器 ( ϕ d \phi_d ϕd) 竞争:
min ϕ g , ϕ e max ϕ d L ( ϕ d , ϕ e , ϕ g ) : = E ( a , x ) ∼ p A X [ E z ∼ p ϕ e ( ⋅ ∣ a , x ) [ log ϕ d ( z , a , x ) ] ⏟ log ϕ d ( ϕ e ( a , x ) , a , x ) ] + E z ∼ p Z [ E ( a , x ) ∼ p ϕ g ( ⋅ ∣ z ) [ log ( 1 − ϕ d ( z , a , x ) ) ] ⏟ log ( 1 − ϕ d ( z , ϕ g ( z ) ) ) ] , \min_{\phi_g,\phi_e}\max_{\phi_d}{\mathcal{L}(\phi_d, \phi_e, \phi_g)} := \mathbb{E}_{(a, \bm{x}) \sim p_{AX}}[\underbrace{\mathbb{E}_{\bm{z} \sim p_{\phi_e}(\cdot \mid a, \bm{x})}[\log \phi_d(\bm{z}, a, \bm{x})]}_{\log \phi_d(\phi_e(a, \bm{x}), a, \bm{x})}] + \mathbb{E}_{\bm{z} \sim p_{Z}}[\underbrace{\mathbb{E}_{(a, \bm{x}) \sim p_{\phi_g}(\cdot \mid \bm{z})}[\log (1-\phi_d(\bm{z}, a, \bm{x}))]}_{\log (1-\phi_d(\bm{z}, \phi_g(\bm{z})))}], ϕg,ϕeminϕdmaxL(ϕd,ϕe,ϕg):=E(a,x)∼pAX[logϕd(ϕe(a,x),a,x) Ez∼pϕe(⋅∣a,x)[logϕd(z,a,x)]]+Ez∼pZ[log(1−ϕd(z,ϕg(z))) E(a,x)∼pϕg(⋅∣z)[log(1−ϕd(z,a,x))]], 其中 p A X p_{AX} pAX 表示拓扑 A A A 和采样节点属性 X X X ( a ∈ A a\in A a∈A, x ∈ X \bm{x} \in X x∈X) 的联合分布。
接近度可以捕获社区内的潜在关系。然而,现实世界中稀疏连接的网络不能提供足够的边。网络中的属性不能通过接近度来衡量。为了解决该限制,ProGAN (Proximity Generative Adversarial Network ) [88] 从一组实例化的三元组中对每个节点的邻近进行编码,以便在低维空间中发现和保存社区关系。
CommunityGAN (Community Detection with Generative Adversarial Nets) [89] 是一个针对重叠社区提出的方法,它通过为每个「节点-社区对」分配一个非负因子来获得节点表示。 其目标函数通过一个 motif 级生成器( ϕ g ( ⋅ ∣ v i ; Θ g ) \phi_g(\cdot|v_i;\Theta_g) ϕg(⋅∣vi;Θg))和判别器( ϕ d ( ⋅ , Θ d ) \phi_d(\cdot,\Theta_d) ϕd(⋅,Θd))进行优化:
min Θ g max Θ d L ( ϕ g , ϕ d ) = ∑ i ( E C ′ ∼ p t r u e ( ⋅ ∣ v i ) [ log ϕ d ( C ′ ; Θ d ) ] + E V ′ ∼ ϕ g ( V ′ ∣ v i ; Θ g ) [ log ( 1 − ϕ d ( V ′ ; Θ d ) ] ) , \min_{\Theta_g}\max_{\Theta_d}{\mathcal{L}(\phi_g, \phi_d)} = \sum_i \left( \mathbb{E}_{C' \sim p_{true}(\cdot \mid v_{i})} \left[\log \phi_d(C'; \Theta_d) \right] + \mathbb{E}_{V' \sim \phi_g(V' \mid v_i ; \Theta_g)}\left[\log (1-\phi_d(V'; \Theta_d) \right]\right), ΘgminΘdmaxL(ϕg,ϕd)=i∑(EC′∼ptrue(⋅∣vi)[logϕd(C′;Θd)]+EV′∼ϕg(V′∣vi;Θg)[log(1−ϕd(V′;Θd)]), 其中 Θ g \Theta_g Θg 和 Θ d \Theta_d Θd 统一了生成器和判别器中节点 v i v_i vi的所有非负表示向量, V ′ ⊆ V V'\subseteq V V′⊆V表示节点子集, C ′ C' C′表示motifs(即派系),条件概率 p t r u e ( C ′ ∣ v i ) p_{true}(C'| v_i) ptrue(C′∣vi)描述了覆盖 v i v_i vi 的 C ′ C' C′ 在所有其他motifs C ′ ∈ C ′ C'\in \mathcal{C'} C′∈C′上的偏好分布。
8 基于自编码器AE的社区发现
自编码器(AE)是最常被用于无监督社区发现的模型,社区发现中常见的AE变体包括堆叠AE、稀疏AE、去噪AE、卷积AE、变分AE。AE 能够描绘非线性、有噪声的现实世界网络并产生平滑的表示。AE [90] 的通用框架由编码器 Z = ϕ e ( A , X ) Z = \phi_e(A,X) Z=ϕe(A,X) 和解码器 X ′ = ϕ r ( Z ) X' = \phi_r(Z) X′=ϕr(Z)构成。编码器 ( ϕ e \phi_e ϕe) 将高维网络结构 ( A A A) 和可获取的属性 ( X X X) 映射到低维潜在特征空间 ( Z Z Z)。解码器 ( ϕ r \phi_r ϕr) 则根据编码器得到的表示 ( H H H) 进行网络重构( Z Z Z),其中 X ′ X' X′ 继承了 A A A 和 X X X 中的首选信息。损失函数 L ( x , ϕ r ( ϕ e ( x ) ) ) \mathcal{L}(\bm{x}, \phi_r(\phi_e(\bm{x}))) L(x,ϕr(ϕe(x)))最大化源数据 x \bm{x} x 和解码数据 ϕ r ( ϕ e ( x ) ) \phi_r(\phi_e(\bm{x})) ϕr(ϕe(x)) 之间的似然。
8.1 基于堆叠自编码器的社区发现
由于单个 AE 不能满足社区发现的要求,堆叠 AE 由一组 AE 堆叠在多个隐藏层中而形成。如图 9 所示,堆栈中的每个编码器分别代表一种类型的输入数据。这些基于堆叠AE的社区发现方法可以灵活地广泛应用于不同场景,例如用于快速演化的动态社区发现 [91]。
semi-DRN (Semi-supervised Nonlinear Reconstruction Algorithm with DNN) [92] 是基于堆叠 AE 的社区发现模型,其中模块度矩阵学习 AE 中的非线性节点表示, k k k-means 获得最终的社区结构。给定邻接矩阵 A = [ a i j ] A=[a_{ij}] A=[aij] 中节点 v i v_i vi 和 v j v_j vj 之间的边,模块度矩阵 B B B 中的模块度值 b i j = a i j − k i k j 2 m b_{ij} = a_{ij} - \frac{k_i k_j}{2m} bij=aij−2mkikj 被优化为最大值[93]。 基于节点表示对节点成对相似性(社区归属)进行编码,成对嵌入矩阵 O = [ o i , j ∈ { 0 , 1 } ] O = [o_{i,j}\in \{0,1\}] O=[oi,j∈{0,1}]同时被定义为提供节点 v i v_i vi 和 v j v_j vj属于 ( o i , j = 1 o_{i,j} = 1 oi,j=1) 或不属于 ( o i , j = 0 o_{i,j} = 0 oi,j=0) 同一社区的先验知识。 因此,通过最小化以下损失函数来优化 semi-DRN 的学习过程:
L = L ( B , X ′ ) + λ L ( O , Z ) , \mathcal{L} = \mathcal{L}(B, X') + \lambda \mathcal{L}(O,Z), L=L(B,X′)+λL(O,Z), 其中 X ′ X' X′ 表示通过一系列 AE 在堆叠表示 ( { H ( l ) } \{H^{(l)}\} {H(l)}) 上解码的网络特征, λ \lambda λ 表示 AE 重构损失 L ( B , X ′ ) \mathcal{L}(B, X') L(B,X′) 和成对约束 L ( O , Z ) \mathcal{L}(O,Z) L(O,Z) 之间的调整权重, L ( O , Z ) \mathcal{L}(O,Z) L(O,Z)测量堆叠 AE 内的每对社区归属 o i j o_{ij} oij 和潜在表示 ( z i , z j ) (\bm{z}_i,\bm{z}_j) (zi,zj)。
类似地,DNE-SBP (Deep Network Embedding with Structural Balance Preservation) [94] 根据符号网络的成对约束进行权重调整,通过区分正负连接使堆叠 AE 将最近的节点聚集在一起。UWMNE (Unified Weight-free Multicomponent Network Embedding ) 及其具有局部增强功能的变体 WMCNE-LE [95] 从网络拓扑和语义信息中保留社区属性,并从局部网络结构的角度整合深度 AE 中的各种信息。
为了发现随时间变化的动态社区结构,sE-Autoencoder (Semi-supervised Evolutionary Autoencoder) [96] 在进化聚类框架内开发,假设前一时刻的社区结构连续指导当前时刻的检测。为此,sE-Autoencoder 在 [92] 的目标函数中添加了时间平滑正则化 L ( Z ( t ) , Z ( t − 1 ) ) \mathcal{L}(Z_{(t)}, Z_{(t-1)}) L(Z(t),Z(t−1)) 以进行最小化:
L = L ( S ( t ) , X ( t ) ′ ) + λ L ( O , Z ( t ) ) + ( 1 − λ ) L ( Z ( t ) , Z ( t − 1 ) ) , \mathcal{L} = \mathcal{L}(S_{(t)}, X'_{(t)})+ \lambda \mathcal{L}(O, Z_{(t)}) +(1-\lambda) \mathcal{L}(Z_{(t)}, Z_{(t-1)}), L=L(S(t),X(t)′)+λL(O,Z(t))+(1−λ)L(Z(t),Z(t−1)), 其中重构误差 L ( S ( t ) , X ( t ) ′ ) \mathcal{L}(S_{(t)}, X'_{(t)}) L(S(t),X(t)′) 最小化 t t t时刻的相似性矩阵 S ( t ) S_{(t)} S(t) 和解码特征 X ( t ) ′ X'_{(t)} X(t)′ 的损失,参数 λ \lambda λ 随 t t t时刻的图表示 Z ( t ) Z_{(t)} Z(t)控制节点成对约束 L ( O , Z ( t ) ) \mathcal{L}(O, Z_{(t)}) L(O,Z(t)) 和时间平滑度正则化。
对于属性网络,DANE (Deep Attributed Network Embedding) [97] 设计了一个两分支 AE 框架:一个分支将高度非线性的网络结构映射到低维特征空间,另一个分支协同学习节点属性。由于相似的节点更有可能聚集在同一社区中,DANE 通过表示学习中的一系列关于网络拓扑和属性信息的邻近度来衡量这些相似性,其中优化应用于一阶邻近度 ( L f \mathcal{L}_f Lf) 、高阶邻近度 ( L h \mathcal{L}_h Lh) 和语义邻近度 ( L s \mathcal{L}_s Ls)的重构损失,以及一致和互补表示的负对数似然控制 ( L c \mathcal{L}_c Lc)。
Transfer-CDDTA (Transfer Learning-inspired Community Detection with Deep Transitive Autoencoder ) [98] 将无监督迁移学习应用于 CDDTA 算法,该算法计算 AE 嵌入实例的 KL 散度,以确保在学习低维表示时,不同域之间的差异(例如,偏移分布、不平衡特征和缺乏样本)可以近似相等。为了将社区信息映射到一个平滑的特征空间,CDDTA 通过相似性矩阵( S s S_s Ss 和 S t S_t St)将输入邻接矩阵 ( A A A) 分为源域 ( s s s) 和目标域 ( t t t),以保持每个堆叠 AE中节点的成对相似度值。然后,Transfer-CDDTA 将域独立特征结合到以下最小化学习过程中:
L = L s ( S s , X s ′ ) + L t ( S t , X t ′ ) + α L K L ( Z s , Z t ) + β L ( Θ ; γ ) , \mathcal{L} = \mathcal{L}_s(S_s, X'_s) +\mathcal{L}_t(S_t, X'_t) + \alpha \mathcal{L}_{KL}(Z_s,Z_t)+\beta\mathcal{L}(\Theta; \gamma), L=Ls(Ss,Xs′)+Lt(St,Xt′)+αLKL(Zs,Zt)+βL(Θ;γ), 其中 α \alpha α, β \beta β, γ \gamma γ 是输入到算法中的权衡参数, L s \mathcal{L}_s Ls 和 L t \mathcal{L}_t Lt表示源域和目标域的重建损失, L K L \mathcal{L}_{KL} LKL 平滑两个域上编码特征( Z s Z_s Zs, Z t Z_t Zt)的 KL 散度, L ( Θ ) \mathcal{L}(\Theta) L(Θ) 是减少优化中过度拟合的可训练变量的正则化项。
DIME (Deep alIgned autoencoder-based eMbEdding) [99] 是为异构社交网络的多个对齐结构设计的堆叠AE模型。它使用元路径来表示不同的关系(异构链接 A i j \mathcal{A}_{ij} Aij,即多个对齐网络 G i \mathcal{G}_i Gi和 G j \mathcal{G}_j Gj之间的锚链接)和各种属性信息( X = { X i } \mathcal{X}=\{X_i\} X={Xi})。相应地,为每个元路径开发一组元邻近度测量,并将相近的节点嵌入到低维潜在特征空间中的一个相近区域,相对较近的区域即为检测的社区。
8.2 基于稀疏自编码器的社区发现
稀疏性普遍存在于现实世界的网络中,并导致社区发现算法的计算困难。为了解决这一问题,稀疏 AE [100] 在隐藏层 h \bm{h} h 中引入了稀疏惩罚 Ω ( h ) \Omega(\bm{h}) Ω(h)。 重构损失函数如下:
L ( x , ϕ r ( ϕ e ( x ) ) ) + Ω ( h ) 。 \mathcal{L}(\bm{x}, \phi_r(\phi_e(\bm{x})))+\Omega(\bm{h})。 L(x,ϕr(ϕe(x)))+Ω(h)。 GraphEncoder (Autoencoder-based Graph Clustering Model) [101] 是第一个使用 AE 进行图聚类的研究。 它通过作为以下损失函数(最小化)的一部分的稀疏项来处理稀疏性:
L ( Θ ) = ∑ i n ∥ h i − x i ∥ 2 + β Ω ( ρ ∥ 1 n ∑ i n h i ) , \mathcal{L}(\Theta)=\sum^n_i\|\bm{h}_{i}-\bm{x}_{i}\|_{2}+\beta \Omega(\rho \| \frac{1}{n}\sum^n_i \bm{h}_i), L(Θ)=i∑n∥hi−xi∥2+βΩ(ρ∥n1i∑nhi),其中权重参数 β \beta β 控制配置值 ρ \rho ρ的稀疏惩罚 Ω ( ⋅ ∥ ⋅ ) \Omega(\cdot\|\cdot) Ω(⋅∥⋅)和隐藏层激活值的平均值。 GraphEncoder 提高了大规模网络的聚类效率,并证明了稀疏网络可以为表示提供足够的结构信息。
Dfuzzy (Deep Learning-based Fuzzy Clustering Model) [102] 用于并行处理框架下稀疏大规模网络中的重叠社区发现。Dfuzzy 引入了针对头节点的堆叠稀疏 AE,以基于模块度发现重叠和非重叠的社区。Dfuzzy 的性能比非深度学习基线高 63%(modularity)、34%(conductance)和 21%(partition coefficient)。
CDMEC (Community Detection Method via Ensemble Clustering) [103] 的社区发现方法将稀疏 AE 与迁移学习模型相结合,以从局部网络结构中发现更多有价值的信息。 为此,CDMEC 构建了四个相似性矩阵,并采用迁移学习通过 AE 的参数共享局部信息。 共识矩阵(consensus matrix)被用于聚合社区发现结果,这些结果由四个相似性矩阵单独产生并由 k k k-means 支持。 最终社区是基于共识矩阵的分解而全局确定的。
8.3 基于降噪自编码器的社区发现
降噪过程减去了 DNN 层内的噪声。 降噪 AE [104] 能够处理损坏的输入数据 ( x ~ \tilde{\bm{x}} x~) 并最小化去噪数据 ( x \bm{x} x) 和解码数据之间的重构损失:
L ( x , ϕ r ( ϕ e ( x ~ ) ) ) 。 \mathcal{L}(\bm{x}, \phi_r(\phi_e(\tilde{\bm{x}})))。 L(x,ϕr(ϕe(x~)))。 DNGR (Deep Neural Networks for Graph Representation) [105] 是在具有 3 个隐藏层的堆叠降噪自编码器框架中设计的。DNGR 应用堆叠降噪编码器来增加发现社区时捕获局部结构信息的鲁棒性。具体来说,它通过随机遍历社区来生成概率共现矩阵,并将其转换为移位的正逐点 MI 矩阵作为输入。
对于损坏的节点属性,GRACE (GRAph Clustering with dynamic Embedding) [106] 是一个非线性多层 DNN 的降噪 AE,由邻域内的影响传播引导,以发现动态变化的社区间活动,通过自训练聚类达到了有效的社区发现性能。
MGAE (Marginalized Graph AutoEncoder ) [104] 对图的属性和结构进行降噪,以通过边缘化过程改进社区发现。它在 m 次内获得损坏的特征 X ~ \widetilde{X} X 。MGAE训练中的目标函数定义为:
L = 1 m ∑ i = 1 m ∥ X − D ~ − 1 2 A ~ D ~ − 1 2 X ~ W ∥ 2 + λ L ( W ) , \mathcal{L} = \frac{1}{m}\sum_{i=1}^m\|X-\widetilde{D}^{-\frac{1}{2}} \widetilde{A} \widetilde{D}^{-\frac{1}{2}} \widetilde{X} W\|_2+\lambda \mathcal{L}(W), L=m1i=1∑m∥X−D −21A D −21X W∥2+λL(W),其中 L ( W ) \mathcal{L}(W) L(W) 表示系数为 λ \lambda λ的参数 W W W的正则化项。
8.4 基于卷积自编码器的社区发现
将 GCN 引入 AE 是一个巨大的成功,因为 GCN 提供了高阶图正则化,而 AE 缓解了 GCN 中的过度平滑问题。 例如,基于 GCN 的无监督社区检测 (GUCD) 方法 [107] 采用半监督 MRF 作为 GCN 中的卷积层(即MRFasGCN,详细信息见5.2小节)[11] 作为其编码器,并提出了一种以社区为中心的双重解码器来检测属性网络中的社区。具体来说,GUCD使用一个解码器重构网络拓扑,另一个解码节点属性,以直接识别社区结构。
SDCN (Structural Deep Clustering Network) [108] 设计了一个传递算子来在 DNN 层上连接 AE 和 GCN,从而使图卷积可以完全支持 AE 的结构表示。当 SDCN 将结构信息集成到深度聚类中时,它通过分别对 AE 和 GCN 应用双重自监督优化来更新社区。
O2MAC (One2Multi Graph Autoencoder for Multi-view Graph Clustering ) [109] 是一种针对多视图属性图的,由单视图到多视图 (One2Multi) 的图聚类 AE。它由一个编码器和多个解码器组成。在编码器中,应用 GCN 来嵌入一组视图分隔图。同时将解码器分别分配给这些单视图,并与编码器共同选择包含信息最多的单视图。O2MAC 能够捕获多视图之间的共享特征,并通过自训练优化改进聚类结果。
8.5 基于图注意力自编码器的社区发现
该类别的社区发现方法不是集成 GCN,而是将 GAT 应用于 AE。DAEGC (Deep Attentional Embedded Graph Clustering) [110] 采用 GAT 作为编码器对邻域内属性节点的重要性进行排序,利用高阶邻域来聚类社区。
多视图网络有两种基于 GAT 和 AE 的社区发现方法。MAGCN (Multi-View Attribute Graph Convolution Networks ) [111] 设计了一个双路径编码器:第一个路径使用能够去噪的多视图属性 GAT 进行编码,第二个路径设计了一个编码器以在多视图属性上获得一致的嵌入。因此,MAGCN 为社区发现任务去除了噪声和分布方差。DMGC (Deep Multi-Graph Clustering) [112] 引入了 AE 来表示每个图的注意力系数,多个图的节点嵌入将通过跨图质心聚类以获得 Cauthy 分布上的社区。
8.6 基于变分自编码器的社区发现
变分自动编码器(VAE)是基于变分推理(如特征的均值和协方差)的 AE 的扩展[113]。它由变分图自编码器(VGAE)[114] 首次引入图学习领域,它假设高斯分布并应用 GCN 作为编码器。基于 VAE 的社区发现由 SBM 等模型激活,以快速推断节点表示中的社区归属 [115]。推理过程考虑了网络的不确定性[116]、[117],例如连接多个社区的边界节点的邻居之间的社区矛盾。VAE 还可以处理社区发现的稀疏性问题。同时,VAE 很容易与更深层次的非线性关系信息相结合。例如,TGA/TVGA (Triad Variational Graph Autoencoder ) [118] 用新的 triad 解码器替换了 VAE/VGAE 的解码器,它描述了现实世界的社区中现有的三元闭包属性。
VGECLE (Variational Graph Embedding and Clustering with Laplacian Eigenmaps) [116] 将图表示分为均值和协方差,同时检测社区,表明每个节点与其真实地理位置的隐式关系的不确定性。借助高斯混合先验和Teacher-Student (T-S) 正则化,VGECLE 旨在让节点 v i v_i vi(student)学习接近其邻居(teacher)的分布。
DGLFRM (Deep Generative Latent Feature Relational Model ) [115] 和LGVG ( Ladder Gamma Variational Autoencoder for Graphs) [119] 进一步捕捉每个节点的社区归属强度。DGLFRM 包括一个基于 GCN 的用于生成节点嵌入的非线性编码器,和一个用于在重叠社区上估计链接概率的非线性解码器。DGLFRM 通过 Beta-Bernoulli 过程对稀疏节点嵌入进行建模,该过程还可以推断社区的数量。LGVG 旨在学习多层和伽马分布的嵌入,以便发现多粒度的社区,即底层的细粒度社区和顶层的粗粒度社区。
为了从社区结构中捕获高阶特征,VGAECD (Variational Graph Autoencoder for Community Detection) [117] 采用高斯混合模型和社区分配参数来概括网络生成过程。VGAECD 通过使用两层 GCN 将观察到的数据编码为潜在嵌入进行优化,以实现证据下界 (ELBO) 最大化。由于 VGAECD 导致了次优的社区发现结果,VGAECD-OPT (OPTimizing Variational Graph AutoEncoder for Community Detection) [116] 提出了一种双重优化,它最小化了二元交叉熵的重构损失和期望最大化算法的社区损失。
ARGA (Adversarial Regularized Graph Autoencoder) 和 ARVGA (Adversarially Regularized Variational Graph Autoencoder ) [120] ,继承了GAN 和 VGAE 的特性,通过将 GAN 的机制引入GAE/VGAE 训练,并在附加的正则化项中优化。
9 基于深度非负矩阵分解的社区发现
非负矩阵分解[121]旨在将一个矩阵分解成两个小的非负矩阵,该方法具有高度的可解释性,能够发现如何将节点分配给社区。应用于社区发现的基本 NMF 模型将邻接矩阵 ( A A A) 分解为两个非负矩阵 ( U ∈ R n × k U\in \mathbb{R}^{n\times k} U∈Rn×k和 P ∈ R k × n P\in \mathbb{R}^{k\times n} P∈Rk×n),其非负约束为 P ≥ 0 P\geq 0 P≥0 和 U ≥ 0 U\geq 0 U≥0。矩阵 U U U 对应于原始网络和社区归属空间之间的映射。矩阵 P = [ p i j ] P = [p_{ij}] P=[pij] 的每一列表示节点 v i v_i vi 属于社区 C j C_j Cj 的归属强度为概率 p i j p_{ij} pij。NMF 适用于非重叠和重叠的社区发现。由于现实世界的网络包含复杂的拓扑信息,传统的 NMF 无法完全揭示它们来检测社区。受深度学习成功的启发,人们对深度 NMF [122] 进行了广泛的研究,它堆叠多层 NMF ( { U 1 , ⋯ , U p } \{U_1,\cdots,U_p\} {U1,⋯,Up}) 以捕获各个级别/方面的节点成对相似性。
在深度社区发现中,DANMF (Deep Autoencoder-like Nonnegative Matrix Fatorization) [123]是无监督学习环境下影响最大的模型。与传统的基于NMF的社区发现方法映射简单的社区成员不同,DANMF使用AE框架在分层映射上进行网络重构。社区归属 P p P_p Pp 的学习目标和分层映射 { U i } 1 p \{U_i\}^p_1 {Ui}1p 通过结合重构损失和 λ \lambda λ加权图正则化进行训练:
min P p , U i L ( P p , U i ) = ∥ A − U 1 ⋯ U p P p ∥ F 2 + ∥ P p − U p T ⋯ U 1 T A ∥ F 2 + λ t r ( P p L P p T ) , s.t. P p ≥ 0 , U i ≥ 0 , ∀ i = 1 , ⋯ , p \min_{P_p,U_i} \mathcal{L}(P_p,U_i) = \|A - U_1\cdots U_p P_p\|_F^2 +\|P_p - U_p^T\cdots U_1^T A\|_F^2 + \lambda tr(P_p L P_p^T), \quad \text{s.t.} ~~ P_p \geq 0, U_i \geq 0, \forall i=1,\cdots,p Pp,UiminL(Pp,Ui)=∥A−U1⋯UpPp∥F2+∥Pp−UpT⋯U1TA∥F2+λtr(PpLPpT),s.t. Pp≥0,Ui≥0,∀i=1,⋯,p 其中, ∥ ⋅ ∥ F \|\cdot\|_F ∥⋅∥F 表示 Frobenius 范数, L L L表示图拉普拉斯矩阵,图正则化 [124] 侧重于网络拓扑相似性以聚类相邻节点。进一步的工作 [125] 在上述基于深度 NMF 的社区发现模型中添加了稀疏约束。
尽管深度NMF提供了一种在形成社区的过程中映射多个变量的方案,但是其矩阵分解的计算成本相对较高。为此,研究者们提出了MDNMF (Modularized Deep Nonnegative Matrix Factorization)[126],直接将模块度应用于基本的多层深度学习结构中。模块度矩阵 B 在以下使用社区归属矩阵 O O O 的最大化训练中为目标:
Q = t r ( O T B O ) , s.t. t r ( O T O ) = n . Q = tr(O^{T}BO), \quad \text{s.t.} ~~ tr(O^{T}O) = n. Q=tr(OTBO),s.t. tr(OTO)=n.
通过最小化以下目标函数,最终得到社区 P p P_p Pp 中的节点归属:
L = ∥ A − U 1 ⋯ U p P p ∥ F 2 + α ∥ O − P p T K T ∥ F 2 − β Q + λ t r ( P p L P p T ) , s.t. P p ≥ 0 , U i ≥ 0 , ∀ i = 1 , . . . , p \mathcal{L} = \|A-U_1\cdots U_p P_p\|_F^2 + \alpha \|O-P_{p}^{T} K^{T}\|_F^2 - \beta Q + \lambda tr(P_p L P_p^T), \quad \textrm{s.t.} ~~ \quad P_p \geq 0, U_i \geq 0, \forall i=1,...,p L=∥A−U1⋯UpPp∥F2+α∥O−PpTKT∥F2−βQ+λtr(PpLPpT),s.t. Pp≥0,Ui≥0,∀i=1,...,p 其中 K K K 是一个额外的非负矩阵,结合了模块度信息,因此深度 NMF 可以探索网络拓扑的隐藏特征。
10 基于稀疏滤波的社区发现
稀疏滤波[127]是一种简单的双层学习模型,它可以处理高维的图数据,将高度稀疏的输入表征为低维特征向量。高度稀疏的输入(具有很多 0 元素的 A A A)将被表示为低维特征向量(具有非零值的 h i \bm{h}_i hi)。为了探索节点的社团归属等更深入的信息,深度SF将多个隐层堆叠起来,从而对更多超参数 ( Θ \Theta Θ) 和大量的平滑数据分布( P r ( h i ) Pr(\bm{h}_i) Pr(hi))进行调优。
DSFCD (Community Discovery based on Deep Sparse Filtering) [128]作为一种代表性的方法,可以分为三个步骤:网络表示、社区特征映射和社区发现。 网络表示阶段分别在邻接矩阵 ( A A A)、模块度矩阵 ( B B B) 和两个相似性矩阵 ( S S S 和 S ′ S' S′) 上执行。选择最佳表示输入到深度 SF 中,以获得在每个节点上表示的社区特征映射( h i \bm{h}_i hi) 。同时, h i \bm{h}_i hi 保留了原始网络( A A A)中的节点相似性和潜在社区归属特征。节点成对约束在损失函数中建模:
L = ∑ i ∥ h i ∥ 1 + λ ∑ i distance ( h i , h j ∗ ) , \mathcal{L} = \sum_i \| \bm{h}_{i}\|_1 + \lambda \sum_i \text{distance}(\bm{h}_i, \bm{h}^*_j), L=i∑∥hi∥1+λi∑distance(hi,hj∗), 其中 ∥ ⋅ ∥ 1 \|\cdot\|_1 ∥⋅∥1 是优化稀疏度的 L 1 L_1 L1 范数惩罚, h j ∗ \bm{h}^*_j hj∗ 为节点 v j v_j vj 的最相似表示( h ∗ \bm{h}^* h∗),通过在 Euclidean 或 KL 上计算 distance ( h i , h j ) \text{distance}(\bm{h}_i, \bm{h}_j) distance(hi,hj) 距离得到。在最小化损失上优化学习过程中,相似的节点会聚集到同一社区中。深度 SF 架构在现实世界数据集的实验中具有重要意义,DSFCD 能比 SF 更准确地发现社区结构。
11 公开资源
我们总结了基于深度学习的社区发现研究实验和实践的基本资源,包括基准数据集、评估指标和开源实现代码(见下表)。
| 方法 | URL |
|---|---|
| CommunityGAN [89] | https://github.com/SamJia/CommunityGAN |
| ARGA [120] | https://github.com/Ruiqi-Hu/ARGA |
| MGAE [104] | https://github.com/FakeTibbers/MGAE |
| DIME [99] | http://www.ifmlab.org/files/code/Aligned-Autoencoder.zip |
| AGE [79] | https://github.com/thunlp/AGE |
| O2MAC [109] | https://github.com/songzuolong/WWW2020-O2MAC |
| DMGC [112] | https://github.com/flyingdoog/DMGC |
| semi-DRN | http://yangliang.github.io/code/DC.zip |
| AGC [78] | https://github.com/karenlatong/AGC-master |
| NOCD [74] | https://github.com/shchur/overlapping-community-detection |
| LGNN [71] | https://github.com/zhengdao-chen/GNN4CD |
| DMGI [82] | https://github.com/pcy1302/DMGI |
| MAGNN [83] | https://github.com/cynricfu/MAGNN |
| DNE-SBP [94] | https://github.com/shenxiaocam/Deep-network-embedding-for-graph-representation-learning-in-signed-networks |
| GraphEncoder [101] | https://github.com/zepx/graphencoder |
| DGLFRM [115] | https://github.com/nikhil-dce/SBM-meet-GNN |
| DANE [97] | https://github.com/gaoghc/DANE |
| SDCN [108] | https://github.com/bdy9527/SDCN |
| CayleyNet [80] | https://github.com/amoliu/CayleyNet |
| DNGR [105] | https://github.com/ShelsonCao/DNGR |
| SEAL [85] | https://github.com/yzhang1918/kdd2020seal |
11.1 数据集
现实世界的数据集和合成数据集都被广泛应用。社区发现实验中的真实世界数据集是从真实世界的应用中收集的,能够从实际应用的角度测试所提出方法的性能。合成数据集由特定模型根据手动设计的规则生成,这些数据集可以测试特定功能。
现实世界数据集
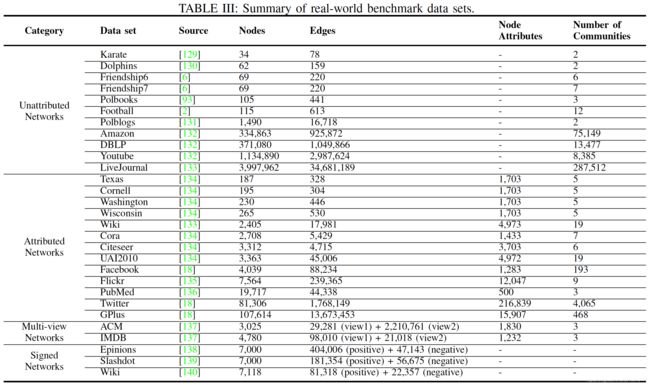
最流行的现实世界数据集可以分为引用/合著网络、社交网络(在线和离线)、生物网络、网页网络、产品共同购买网络等。原文表 III 总结了各种形态网络(即无属性、有属性、多视图、带符号)的典型数据集。数据集相关说明及下载地址详见原文附录 B。
人工合成数据集
GN网络 [2]:经典的 GN 基准网络由 128 个节点组成,分为 4 个社区,其中每个社区有 32 个节点,每个节点共享一个固定的平均度( k i n k_{in} kin),并连接另一个社区中预定义数量的节点 ( k o u t k_{out} kout)。 例如, k i n + k o u t = 16 k_{in} + k_{out} = 16 kin+kout=16。参数 ( μ \mu μ) 用于控制每个节点在其他社区中的邻居比例。
LFR网络 [142]:LFR 基准数据集模拟现实世界网络中节点的度和网络的无标度性质。社区验证更具挑战性,结果更有说服力。LFR 生成程序提供了一组丰富的参数,通过这些参数可以控制网络拓扑,包括网络大小 ( n n n)、平均度 ( k k k) 和最大度 ( M a x k Maxk Maxk) 、社区规模对最小值 ( M i n c Minc Minc) 和最大值 ( M a x c Maxc Maxc) ,以及混合参数 ( μ \mu μ)。节点度由指数为 τ 1 \tau_1 τ1 和 τ 2 \tau_2 τ2 的幂律控制。LFR 在网络结构中比GN 基准网络更复杂,它可以生成更灵活的网络,是传统社区发现研究中最常见的模拟基准。
11.2 评价指标
本节总结了主流的评估指标,并在表 IV 中进行了归纳。详细的评估指标介绍参见原文附录 C 。
12 实际应用
如图 10 所示,社区发现技术已被应用于各种各样的任务和领域,例如:
-
推荐系统:社区结构对于基于图的推荐系统起着至关重要的作用[143][144],因为社区成员可能具有相似的兴趣和偏好。 通过检测节点之间的关系(即用户-用户、项目-项目、用户-项目),CayleyNets [80] 和 UWMNE/WMCNE-LE [95] 等模型可以产生高质量的推荐。
-
生物化学:在该领域中,节点代表化合物和分子图中的蛋白质或原子,边代表它们之间的交互。社区发现可以识别在器官中起作用的新蛋白的免疫复合物[8][101]、化合物,或疾病的病理因素(如基于社区的肺癌检测 [146] )。对于基因组数据集上的各种肿瘤类型,之前的研究 [147] 揭示了社区存活率与社区中肿瘤类型分布之间的相关性。
-
在线社交网络:分析在线社交活动可以识别在线社区,并将它们与现实世界联系起来。Facebook、Twitter 和 LinkedIn 等在线社交网络[2]揭示了在线用户之间相似的兴趣,从而自动识别出个人的偏好。同时,社区发现技术可以用于在线隐私保护[148] ,基于在线社会行为识别罪犯 [149]等场景,这些犯罪分子支持和传播犯罪思想,甚至可能从事恐怖主义活动 [150]。
-
社区欺骗:为了绕开社区发现,我们可以通过社区欺骗技术[151]覆盖 Facebook 等社交网络中的一组用户。有的社区欺骗活动对虚拟社区有害,也有的社区欺骗活动是出于正当利益的考虑。从基于社区的结构熵中,残差熵最小化(REM)有效地躲避了社区发现算法[152]。 [153]在大型网络中对社区发现对欺骗的鲁棒性进行了系统评估。
-
社区搜索:社区搜索旨在搜索依赖于社区结构的节点 [16]。例如,搜索用户所在兴趣社区的其他成员。这些社区是根据用户的兴趣临时形成的,有几种实践应用于此场景。 本地社区搜索 [15] 一次假设一个查询节点并扩展它周围的搜索空间。该策略将反复尝试,直到社区找到所有归属。Attributed Truss Communities (ATC) [154] 将查询节点上的社区与相似的查询节点属性互连起来。
13 未来方向
尽管深度学习极大促进了社区发现领域研究的繁荣,但是目前仍然存在许多有待解决的问题:
13.1 未知的社区数量
挑战:现实世界中存在大量无标签数据,因此社区的数量是未知的。现有的无监督社区发现方法要求我们事先指定需要检测出的社区数量,而这往往是不可行的。我们需要使用一种有效的方法来处理由于缺乏这种知识而造成的情况。
机遇:网络拓扑结构的分析提供了应对这一挑战的潜在解决方案,并且已经有学者进行了一些研究工作 [102]。通常,这些方法执行随机游走以获得初步社区并通过模块度改进检测结果。但是实践中遇到不联通的网络时,随机游走不能涉及每个节点,并且会降低检测性能。因此,这一问题需要更完整的解决方案和进一步的研究。
13.2 社区嵌入
挑战:传统的节点嵌入方法会保留直接相连或在低维空间中拥有许多共同邻居的节点,但是在学习过程中却很少利用社区结构[155]。为此,社区发现需要引入能够感知社区结构的学习过程来表征社区信息[156]。
机遇:迄今为止,很少有工作将社区嵌入集成到深度学习模型中,因此需要在该领域做更多努力。一般而言,由于为社区生成表示的社区嵌入可能会带来额外的计算成本,因此未来的工作需要开发以计算为目标的快速算法。此外,由于嵌入结果依赖于超参数优化,如何将特殊的优化机制设计到深度社区发现模型中是另一个关键方面。
13.3 层次化网络
挑战:Web 等网络通常具有组织不同层次社区的树状结构。因此,社区发现需要具有从低到高的层次化过程。
机遇:传统方法通常遵循以下三种工作路线之一:(1) 直接一次性估计层次结构,(2) 以自下而上的方式合并社区, (3) 以自上而下的方式拆分社区。它们的性能受到大量参数或对网络密度的严格要求的限制[157]。最近的工作表明网络嵌入对该问题的效率有影响 [158], [159]。社区发现方法在保留社区层次结构的同时,还需要充分利用高层和低层社区之间的包含关系[159]。由于在学习嵌入时处理隐含关系的能力很强,我们相信对深度学习的深入研究可以促进层次社区发现的发展。
13.4 多层网络
挑战:在我们的自然环境中很容易观察到,作为家人的两个人同时也是朋友,不同的交通方式将地方连接起来。实体总是以多种方式相互交互[160]。多层网络提供了一个通用的多层框架,以将一组实体之间的多种交互类型表征为不同的网络层 [161]。
机遇:与单层网络中社区发现工作的繁荣发展不同,多层网络的研究发展仍处于起步阶段[162]。 多层网络通常将其多层的信息合并到单层中,然后进行单层社区发现。在深度学习的背景下,可以通过深度架构学习网络信息的低维表示,来构建一个类似的解决方案。通常,用于多层社区发现的深度学习方法应适当考虑几个问题:(1)交互类型之间的差异,(2)层间不同程度的稀疏性,(3)跨层可能的连接,(4)方法在层数方面的可扩展性。
13.5 异构网络
挑战:为了准确描述现实,网络需要包含表征不同类型实体之间关系的异构信息 [163],例如演员和电影之间的角色扮演关系。由于缺乏建模复杂结构和语义信息的能力,针对同构网络设计的社区发现方法往往不适用于异构网络,因此需要为异构网络提供新方法。
机遇:元路径是处理不同语义信息的一项研究工作,它描述了所涉及的节点类型之间的复合关系。这允许深度模型通过不同的元路径聚合来自相同类型的其他节点的信息来表示节点,然后基于节点相似性评估进行社区发现 [83][99][137]。 然而,最有意义的元路径的选择仍然是一个待解决的问题。未来可以关注于元路径选择的灵活模式和其他可以利用各种类型关系的新模型上。
13.6 网络异质性
挑战:网络异质性 [164] 指相连的节点也可能从属于不同的社区,或具有不相似的特征。 例如,欺诈者故意与用户建立联系以隐藏自己不被发现。对社区发现任务而言,跨社区相连的边界节点往往具有这种属性。捕获网络异质性可以为社区发现任务提供有价值的信息。
机遇:由于大多数方法严重依赖同质性,假设连接的节点具有更多相似性并且更有可能来自同一社区,因此利用网络异质性的深度学习方法有望获得更好的社区发现性能。
13.7 拓扑不完备的网络
挑战:在现实场景下,并不一定总是能够获取节点之间的关系,因此网络的拓扑结构往往是不完整的[8]。例如,由于监测所有蛋白质之间的相互作用代价昂贵,蛋白质相互相互作用 (PPI) 网络通常是不完整的 [165]。从有限的拓扑信息中获取有意义的社区知识对于这种情况至关重要。
机遇:完整网络拓扑的要求极大地损害了社区发现方法(尤其是基于邻域聚合的方法)在拓扑不完备网络(TIN)上的适用性。为此,应进一步开发具有信息恢复机制的深度学习方法,以便实现准确的社区发现。
13.8 跨域网络
挑战:各个节点之间不同类型的交互可以用不同的网络(域)来描述,正如现实世界中,用户通过 Facebook 和 Twitter 等多个在线社交平台相互交互。由于利用来自相关源域的丰富信息有助于提升网络学习的性能[166],我们可以开发深度学习模型,提升目标域社区发现任务的性能 [98]。
机遇:通过学习源域和目标域的共同潜在表示的域自适应,可以解决以下场景中的许多挑战:(1)缺乏明确的社区结构,(2)没有节点标签,(3)没有社区的groundtruth , (4) 较差的网络结构导致的表示性能不佳, (5) 不适合深度学习模型的小规模网络。在提出具有跨域信息的基于深度学习的社区发现方法时,必须解决应用迁移学习架构的问题,例如跨域系数的测量、分布偏移和计算复杂性。
13.9 多属性视图网络
挑战:现实世界中的网络比实验环境下的网络往往更加复杂[167]。多属性图网络提供了一种根据多个视图描述关系信息的视角,每个视图都包含一种节点属性[168]。利用各个视图之间的互补性,可以提升社区发现的性能[169]。
机遇:一个简单的工作流是组合从每个视图单独学习的表示,但会引入多视图数据的噪声/冗余。为解决此问题,深度学习尝试通过学习社区发现的通用聚类嵌入来提取多个视图之间的一致性信息 [111]。由于多视图节点属性在学习过程中仍然需要更好的集成方案,因此鼓励更多的工作来研究多视图社区检测的全局表示问题以避免次优。
13.10 带符号的网络
挑战:人们越来越注意到并不是所有连接关系都会使节点更接近。比如友谊表示积极的情绪(即喜欢和支持),而敌人则表示消极的态度(即不喜欢)。边的语义关系的区别可以用符号来刻画 [170]。由于正连接和负连接对节点的影响差异较大,以往在无符号网络上设计的社区发现方法并不适用。
机遇:在带符号网络中进行社区发现对主要挑战在于适应负连接。应该利用深度学习技术来正确表示带符号网络中社区发现的正负关系。与正关系不同,基于负关系的不同节点成对约束为学习带符号网络的社区发现的网络嵌入,提供了一种潜在解决方案 [94]。未来的工作可以处理带符号的边,考虑如何使用较少的先验知识。
13.11 动态网络
挑战:网络不是静态的,而是随着急剧变化的网络结构和时序的语义特征而演变的。深度学习模型应该快速捕获网络上发生的变化,以探索社区的演化情况。
机遇:深度学习和社区发现都需要处理不断变化的数据分布和不断发展的数据规模。通过静态网络快照重新训练不是进行动态社区发现的理想解决方案。在我们的文献综述中,只有一项研究通过设计演化的 AE 来发现动态网络中的社区,其旨在通过快照发现平滑变化的社区结构 [96]。动态网络的技术挑战集中在控制模型训练过程中的动态(即空间和时间属性)。动态社区发现的未来方向包括:(1)研究影响社区结构的空间变化;(2)学习具有时间语义特征的深度模式,如节点属性和边上的符号信息;(3)开发深度社区发现方法以处理网络动态并实现快照的鲁棒性。
13.12 大规模网络
挑战:大规模网络可能包含数百万个节点、边和社区等结构模式。它们固有的尺度特征,如无标度[21][171],会影响深学习模型在社区发现任务中的性能。可扩展性是深度学习在大规模网络环境中实现社区检测的关键问题[17]。我们希望开发一种鲁棒而灵活的深度学习方法,从而实现高性能协同计算。
机遇:对于高维网络拓扑矩阵,深度学习中常用的关键降维策略,即矩阵低秩逼近,无法应对大规模网络。即使是当前的分布式计算解决方案仍然过于昂贵。因此,迫切需要在精度和速度方面都远远超过当前基准的新型深度框架、模型和算法。
总结
本研究提供了社区发现方法的全面概述。近十年来,社区发现的发展在很大程度上依赖于深度学习模型,深度学习是社区发现的一个趋势。同时,深度学习影响社区发现的过程,大量研究成果可从具有高影响力的国际会议和被多个领域讨论的同行评审期刊中获得。根据我们的研究,深度学习模型显著提高了社区发现的有效性、效率、稳健性和适用性。与传统的社区发现方法相比,新技术在使用上更加灵活,并且可以在粗略的预处理中利用更大量的数据。我们针对收集的最新文献设计了一个分类法,将其分为六类。在每个类别中,深度学习模型都以社区发现为目标,即编码表示和优化聚类结果。我们讨论了每个深度学习模型对社区发现任务的贡献。此外,我们根据回顾的文献总结并提供了丰富的资源,即数据集、评估指标和开源代码。我们还深入了解了一系列社区发现的实际应用。最后,我们确定了开放的研究方向,以促进该领域的进一步研究。