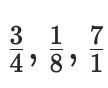【蓝桥杯备赛】2020年第十一届蓝桥杯省赛第二场（10月17日）真题C++ B组 未完待续……

题目结构

项目	题型	分值	题型
第一题	结果填空	5	门牌制作（取位数）
第二题	结果填空	5	既约分数（gcd）
第三题	结果填空	10	蛇形填数（找规律或模拟）
第四题	结果填空	10	跑步锻炼（日期处理）
第五题	结果填空	15	七段码（DFS）
第六题	程序设计	15
第七题	程序设计	20
第八题	程序设计	20
第九题	程序设计	25
第十题	程序设计	25

---

填空题

第一题 门牌制作

小蓝要为一条街的住户制作门牌号。

这条街一共有 20202020 位住户，门牌号从 11 到 20202020 编号。

小蓝制作门牌的方法是先制作 00 到 99 这几个数字字符，最后根据需要将字符粘贴到门牌上，例如门牌 1017 需要依次粘贴字符 1、0、1、71、0、1、7，即需要 11 个字符 00，22 个字符 11，11 个字符 77。

请问要制作所有的 11 到 20202020 号门牌，总共需要多少个字符 22？

---

解法一：excel

1. 用excel生成1-2020的数字
2. 复制到记事本去掉
3. 复制到word替换2为A看有多少个数被替换

解法二：python

ans=0;
for i in range(1,2021):
    ans+=str(i).count('2')
print(ans)

解法三：取位数

思路：取位数

#include 
using namespace std;
int main()
{
    int cnt = 0;
    for (int i = 1; i <= 2020; i++)
    {
        int t = i;
        while (t)
        {
            if (t % 10 == 2)
            {
                cnt++;
            }
            t /= 10;
        }
    }
    cout << cnt;
} // namespace std;

• 如果while循环中放的是i的话会进入死循环，当i=0之后，i加一，i就一直等于1

---

答案：624

---

第二题 既约分数

如果一个分数的分子和分母的最大公约数是 11，这个分数称为既约分数。

例如
， 都是既约分数。

请问，有多少个既约分数，分子和分母都是 1 到 2020 之间的整数（包括 1 和 2020）？

思路：求最大公约数为1

#include 
using namespace std;
int gcd(int a, int b)
{
    if (b == 0)
        return a;
    else
        return gcd(b, a % b);
}
int main()
{
    int cnt = 0;
    for (int i = 1; i <= 2020; i++)
    {
        for (int j = 1; j <= 2020; j++)
        {
            if (gcd(i, j) == 1)
            {
                cnt++;
            }
        }
    }
    cout<<cnt;
}

---

答案：2481215

---

第三题 蛇形填数

如下图所示，小明用从 1 开始的正整数 “蛇形” 填充无限大的矩阵。
在这里插入图片描述

容易看出矩阵第二行第二列中的数是 5，请你计算矩阵中第 20 行第 20 列的数是多少？

解法一：手算

解法二：找规律

思路：看对角线：1，5，14

#include 
using namespace std;

int main()
{
	int w = 4, ans = 1;
	for (int i = 1; i <= 19; i ++)
	{
		ans += w;
		w += 4;
	}
	
	cout << ans << endl;
	return 0;		
}

解法三：模拟

#include
using namespace std;
signed main()
{
    int r = 1 , c = 1 , ans = 1;
    while(r != 20 || c != 20){
        if(r == 1){
            if(c & 1) c ++ ;
            else r ++ , c --;
        }
        else if(c == 1){
            if(r % 2 == 0) r ++;
            else r -- , c ++;
        }
        else if((r + c) % 2) r ++ , c -- ;
        else r -- , c ++ ;
        ans ++ ;
    }
    cout << ans << '\n';
    return 0;
}

---

答案：761

---

第四题 跑步锻炼

小蓝每天都锻炼身体。

正常情况下，小蓝每天跑 1 千米。

如果某天是周一或者月初（1 日），为了激励自己，小蓝要跑 2 千米。

如果同时是周一或月初，小蓝也是跑 2 千米。

小蓝跑步已经坚持了很长时间，从 2000 年 1 月 1 日周六（含）到 2020 年10 月 1 日周四（含）。

请问这段时间小蓝总共跑步多少千米？

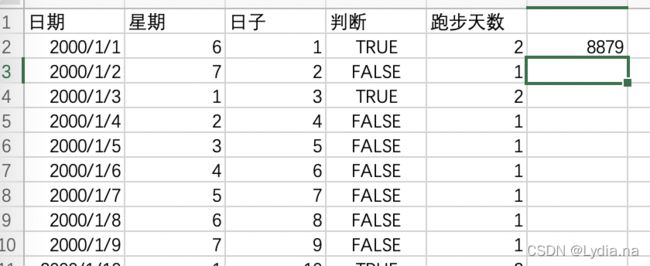
解法一：Excel

1. 求总天数：从2000/1/1填充到2020/10/1 发现有7580项
2. 求周一天数：weekday()函数求出当天单元格的星期，再筛选1的数字 共1083
3. 求1号天数：day()函数求当天单元格，再筛选1的数字 249+1=250
4. 总共跑多少千米？7580+1083+250-34=8879

---

答案：8879

---

解法二：日期处理

1. 用 0 ~ 6 来代表 周一 至 周日；
2. 用 sum 来代表 2000年1月1日 至 某年某月某日 所经过的天数；
3. 由于 2000年1月1日 是周六，那么用 (sum + 5) % 7 就能表示 某年某月某日 是星期几；
4. 因为 2020年10月1日 未处理，所以最后 ans += 2；

#include 
#include 
#include 
using namespace std;
int days[13] = {0,31,28,31,30,31,30,31,31,30,31,30,31};

bool is_leap(int year){
    return year % 400 == 0 || (year % 4 == 0 &&  year % 100 != 0);
}

int get_days(int year,int month){
    if(month==2) return 28+is_leap(year);
    return days[month];
}

int main(){
    int sum=0,ans=0;
    for(int i=2000;i<=2019;i++){
        for(int j=1;j<=12;j++){
            for(int k=1;k<=get_days(i,j);k++){
                int weekday = (sum + 5)%7;
                if(k==1||weekday==0)ans+=2;
                else ans++;
                sum++;
            }
        }
    }
    for (int j = 1; j <= 9; j ++)
		for (int k = 1; k <= get_days(2020, j); k ++)
		{
			int weekday = (sum + 5) % 7;
			if(k == 1 || weekday == 0) ans += 2;
			else ans ++;
			sum ++;
		}			
    cout<<ans+2<<endl;
}

第五题 七段码

题目转化为：有多少种选边方案，使得选出来的边构成的图只有一个联通快。

1. 状态压缩：把a-g转化为0-6，亮灯情况转化为0与1的全排列
2. 深搜是否存在一个连通块儿

#include 
#define MAX 7
using namespace std;
int a[MAX][MAX];    //相邻数组
int b[MAX];     //亮灯数组
int c[MAX];     //映射数组

//初始化数组
void init(){
    a[0][1]=1;
    a[0][5]=1;
    a[1][2]=1;
    a[1][6]=1;
    a[2][3]=1;
    a[2][6]=1;
    a[3][4]=1;
    a[4][5]=1;
    a[4][6]=1;
    a[5][6]=1;
}
//深搜相邻的点并关掉
void dfs(int k){
    c[k]=0;
    for(int i=0;i<MAX;i++){
        //如果i位置与k位置相连
        if(a[i][k]||a[k][i]){
            //如果i位置亮着灯
            if(c[i]){
                //深搜
                dfs(i);
            }
        }
    }
}
bool check(){
    //数组映射
    for(int i=0;i<MAX;i++){
        c[i]=b[i];
    }
    int flag=0;
    for(int i=0;i<MAX;i++){
        //如果i位置亮灯
        if(c[i]){
            //把周围灯都灭掉
            dfs(i);
            //连通块儿数加一
            flag++;
        }
    }
    if(flag==1){
        return true;
    }
    return false;
}
int main(){
    init();
    int sum=0;
    //可能亮1-7段
    for(int i=0;i<MAX;i++){
        //初始化亮灯数组
        memset(b,0,sizeof(b));
        for(int j=7;j>=i;j--){
            b[j]=1;
        }
        do{
            //如果确实是一段
            if(check()){
                sum++;
            }
        }while(next_permutation(b,b+MAX));
    }
    cout<<sum<<endl;
    return 0;
}