【计算方法】实验四:python实现拉格朗日插值和牛顿插值
文章目录
- 1. lagrange 插值拟合
-
-
- 插值多项式与原函数
-
- 2.newton插值
-
-
- 插值函数与原函数
-
1. lagrange 插值拟合
import numpy as np
import matplotlib.pyplot as plt
from sympy import *
from sympy.plotting import plot
from sympy.abc import x
def lagrange(x,y,x0):
n = len(x)
Ln = 0
for k in range(n): #对插值点循环
Tk = 1
for j in range(n):
if j!=k:
Tk = Tk * (x0-x[j])/(x[k] - x[j])
Ln = Ln + y[k]*Tk
return Ln
x = np.arange(-5,6,1)
y = list(map(lambda i: 1/(1+i**2),x))
x0= symbols('x')
lagrange(x,y,x0)
simplify(lagrange(x,y,x0))
插值得到的多项式:
插值多项式与原函数
x_new = np.arange(-5, 6, 0.1)
f_result = []
x = symbols('x')
for i in x_new:
f_result.append(f.subs(x,i)) # 把不同的x带入求值
#plt.scatter(x, y, label='data')
plt.plot(x_new, f_result, label='lagrange-nih',linestyle='-.')
plt.plot(x_new, 1/(1+x_new**2),label="Polynomial-100")
plt.legend()
plt.axis([-5,5,-2,2])
plt.show()
| 拉格朗日 | 插值多项式 | 原多项式 |
|---|---|---|
| x = 3.5 | −0.2261962890625 | 0.07547169811320754 |
| x = 4.5 | 1.57872099034926 | 0.047058823529411764 |
2.newton插值
import numpy as np
import matplotlib.pyplot as plt
from sympy import *
from sympy.plotting import plot
from sympy.abc import x
def newton(x,y,x0):
n=len(x)
Nn = y[0] #第一列存函数值
fn = np.ones([n,n]) #初始化差商骨架结构
fn[:,0] = y #差商表第一列
Nj = 1 #连乘的设置为1
for k in range(1,n): #从第二列开始求均差
for j in range(k,n):
fn[j,k] = (fn[j,k-1]-fn[j-1,k-1])/(x[j]-x[j-k]) #改x[j]-x[j-k+1]
Nj = Nj*(x0-x[k-1])
Nn = Nn+fn[k,k]*Nj
return Nn
x = np.arange(-5,6,1)
y = list(map(lambda i: 1/(1+i**2),x))
x0= symbols('x')
f = newton(x,y,x0)
simplify(f)
得到的多项式:
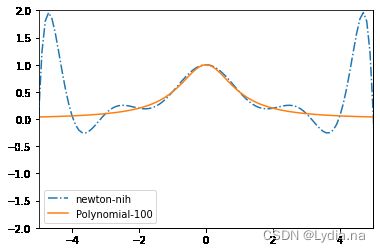
插值函数与原函数
x_new = np.arange(-5, 6, 0.1)
f_result = []
x = symbols('x')
for i in x_new:
f_result.append(f.subs(x,i)) # 把不同的x带入求值
#plt.scatter(x, y, label='data')
plt.plot(x_new, f_result, label='newton-nih',linestyle='-.')
plt.plot(x_new, 1/(1+x_new**2),label="Polynomial-100")
plt.legend()
plt.axis([-5,5,-2,2])
plt.show()
| 牛顿 | 插值多项式 | 原多项式 |
|---|---|---|
| x = 3.5 | −0.226196289062507 | 0.07547169811320754 |
| x = 4.5 | 1.57872099034924 | 0.047058823529411764 |
对于插值多项式得到的值发现与原多项式得到的值差别很大,即插值函数与数据点的趋势不同,这时由于拉格朗日插值的局限性而导出现了Range现象。出现了在等距点插值的高次多项式相关的极端的“多项式摆动”