Bishop 模式识别与机器学习读书笔记_ch1.1 机器学习概述

模式识别与机器学习-读书笔记

第一章 机器学习概述（I）

---

数据模式搜索问题是一个基础性的问题，有着悠久而成功的历史。

• 16世纪对第谷布拉赫的广泛天文观测使约翰内斯开普勒发现了行星运动的经验定律，从而为古典力学的发展提供了跳板。

• 原子光谱中正则性的发现在20世纪初量子物理学的发展和验证中起到了关键作用。

模式识别领域涉及通过使用计算机算法自动发现数据中的规则，并利用这些规则采取行动，例如将数据分类。

例 [手写字体] 如图所示。每个数字对应于28×28像素的图像，因此可以由包含784个实数的向量 $\mathbf{x}$ 表示。我们的目标是建立一个机器(Machine, 可理解为函数集合)，它将以这样一个向量 $\mathbf{x}$ 作为输入，并将产生数字 $0,1,\cdots ,9$ 作为输出的类别。

注解：

（1）因为字迹变化很大，因此这并非一个精确解问题。

（2）若使用手工规则或启发式方法根据笔划形状区分数字，会导致规则和额外规则大量出现，产生糟糕的结果。

1. 机器学习为模式识别提供了一个有效途径

机器学习的两种定义：

（1）机器学习是用数据或以往的经验，以此优化计算机程序的性能标准。

（2）机器学习是对能通过经验自动改进的计算机算法的研究。

采用一种机器学习方法，利用一个称为训练集的 $N$ 个手写字体集合 $\{{\mathbf{x}}_1,{\mathbf{x}}_1,\cdots ,{\mathbf{x}}_N\}$ 来调整自适应模型的参数，可以获得更好的结果。训练集中的数字类别是预先知道的，通常是通过单独检查和手工标记它们。目标向量 $\mathbf{t}$ 来表示数字的类别，目标向量 $\mathbf{t}$ 表示对应数字的身份。稍后将讨论用向量表示类别的适当技术。

注解：对于每个数字图像 $\mathbf{x}$ 有一个这样的目标向量 $\mathbf{t}$，如 $\mathbf{t}=(0,0,1,0,0,0,0,0,0)$表示第二类.

运行机器学习算法的结果可以表示为函数 $\mathbf{y}(\mathbf{x})$，可理解为理想函数。该函数以新的数字图像 $\hat{\mathbf{x}}$ 作为输入，并生成输出向量 $\mathbf{y}$，其编码方式与目标向量相同。函数 $\mathbf{y}(\mathbf{x})$ 的精确形式是在训练阶段（也称为学习阶段）根据训练数据确定的。一旦模型被训练，它就可以确定新的数字图像的身份，这些新的图像被称为测试集。正确分类不同于训练集的新示例的能力称为泛化。在实际应用中，输入向量的可变性使得训练数据只占所有可能输入向量的一小部分，因此泛化是模式识别的中心目标。

在大多数实际应用中，通常对原始输入变量进行预处理，将其转换成一些新的变量空间，这样，模式识别问题就更容易解决。例如，在数字识别问题中，数字的图像通常被转换和缩放，以便每个数字都包含在一个固定大小的框中。这大大减少了每个数字类内的可变性，因为所有数字的位置和比例现在都是相同的，这使得后续的模式识别算法更容易区分不同的类。这种预处理阶段有时也称为特征提取。

注解：新的测试数据必须使用与培训数据相同的步骤进行预处理。

训练数据包含输入向量及其对应目标向量的示例的应用称为有监督学习问题。例如数字识别例子，其目的是将每个输入向量分配给有限个离散类别中的一个，这种情况称为分类问题。如果所需的输出包含一个或多个连续变量，则该任务称为回归。回归问题的一个例子是预测化学生产过程中的产量，其中输入包括反应物浓度、温度和压力。

在其他模式识别问题中，训练数据由一组输入向量 $\mathbf{x}$ 组成，没有任何对应的目标值。这种无监督学习问题的目标可能是在数据中发现一组类似的例子，称为聚类，或者确定数据在输入空间中的分布，称为密度估计，或将数据从高维空间投影到二维或三维，以实现可视化。

尽管每项任务都需要自己的工具和技术，但支持这些任务的许多关键思想对于所有此类问题都是通用的。下面以多项式回归为例来介绍基本的机器学习的处理过程。

2. 多项式回归案例分析

我们首先介绍一个简单的回归问题，我们将在本章中作为一个运行示例来激发一些关键概念。假设我们观察到一个实值输入变量 $x$，我们希望用这个观测值来预测一个实值目标变量 $t$ 的值，考虑使用综合生成的数据的人工示例是有指导意义的，因为我们知道生成数据以与任何学习模型进行比较的精确过程。本示例的数据由目标值函数 $\sin (2\pi x)$ 掺杂随机噪声的生成，即

$t_i=\sin (2\pi x_i)+{\epsilon }_i,i=1,2,\cdots ,N$ 或 $\mathbf{t}=\sin (2\pi \mathbf{x})+\epsilon$

我们需要找出变量 $\mathbf{x}$ 与 $\mathbf{t}$ 之间的真正关系

​ $\mathbf{y}=\sin (2\pi \mathbf{x})$

2.1 多项式回归的数据准备

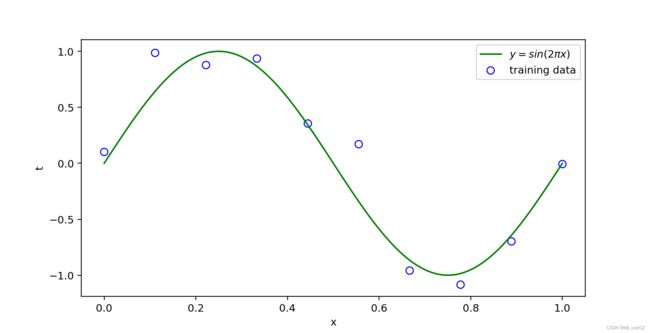
首先我们需要获取一个训练集，它包含了 $x$ 的 $N$ 个观测值，组成一个向量 $\mathbf{x}=(x_1,x_2,\cdots ,x_N{)}^T$，以及相应观测值 $t_i$ ，表示为向量 $\mathbf{t}=(t_1,t_2,\cdots ,t_N{)}^T$. 下面的代码和图显示了一个训练集的图，它包含 $N=10$ 个数据点。图中的输入数据集 $\mathbf{x}$ 是通过选择 $x_n$ 的值生成的，对于 $n=1,2,\cdots ,n$，在 $[0,1]$ 范围内均匀分布，目标数据集 $\mathbf{t}$ 是通过首先计算函数 $\sin (2\pi x)$ 再对每个函数值加上服从正态分布的随机噪声获得的，目的是获得观测值 $t_n$. 通过这种方式生成数据，我们捕捉到了许多真实数据集的一个特性，即它们具有潜在的规律性，我们希望学习这些规律性，但个别观测结果被随机噪声破坏。这种噪声可能来自本质上的随机（即随机）过程，如放射性衰变，但更典型的是由于存在着自身不可观测的可变性来源。

import numpy as np
import matplotlib.pyplot as plt
from math import pi
'''
x = np.linspace(0,1,10)
t = np.sin(2*pi*x)+0.2*np.random.randn(10)

data_p4 = np.array([x,t])
#print(data_p4.shape)
np.save('datap4',data_p4)
'''
data = np.load('datap4.npy')
x = data[0,:]
t = data[1,:]

x_true = np.linspace(0,1,100)
y = np.sin(2*pi*x_true)

plt.figure(dpi=220)
plt.scatter(x,t,facecolor="none", edgecolor="b", s=50, label="training data")
plt.plot(x_true,y,'g-',label='$y=sin(2\pi x)$')
plt.xlabel('x')
plt.ylabel('t')
plt.legend()

plt.show()

生成数据的可视化效果

我们的目标是利用这个训练集来预测一些新变量 $\hat{\mathbf{x}}$ 的目标变量的 $\hat{\mathbf{t}}$ (测试集的输入和输出加上 hat 符号表示测试或者预测). 正如我们稍后将看到的，这涉及到隐式地试图发现底层函数 $\sin (2\pi x)$, 因为已经假设我们并不事先知道这个函数。这在本质上是一个困难的问题，因为我们只能从有限的数据集中归纳出函数。此外，观测数据被噪声污染，那么对于给定的 $\hat{\mathbf{x}}$ 我们并不能确定地给出一个合适的 $\hat{\mathbf{t}}$，这也给后续讨论的概率论提供了以精确和定量的方式表达这种不确定性的框架，以便根据适当的标准做出最优的预测。

2. 多项式拟合

我们将比较非正式地进行讨论，并考虑一种基于曲线拟合的简单方法。特别是，我们将使用多项式函数来拟合数据

KaTeX parse error: Undefined control sequence: \notag at position 116: …x}^T\mathbf{w} \̲n̲o̲t̲a̲g̲ ̲
其中 $M$ 是多项式的阶，$x_j$ 表示 $x$ 的幂为 $j$. 多项式系数 $w_0,w_1,\cdots ,w_M$ 由向量 $\mathbf{w}$ 表示。注意，虽然多项式函数 $y(x,\mathbf{w})$ 是关于变量 $x$ 的非线性函数，但它是关于系数 $\mathbf{w}$ 的线性函数。

注解：在机器学习或者数据分析中，数据 $\mathbf{x} $ 是已知的，系数又称为模型，是未知的，因此称为线性模型。

系数 $\mathbf{w}$ 的值将通过多项式拟合训练数据来确定。这可以通过最小化一个误差函数(又称为损失函数)来实现，该误差函数测量函数 $y(x,\mathbf{w})$ 在任意给定值 $\mathbf{w}$ 和训练集数据点之间的不匹配程度。误差函数的一个简单选择是，用每个数据点 $x$ 的预测 $y(x_n,\mathbf{w})$ 与相应的目标值 $t_n$ 之间的误差平方和给出，这样我们就可以最小化能量函数

$$E(\mathbf{w})=\frac{1}{2}\sum _{n=1}^N\{y(x,\mathbf{w})-t_n{\}}^2$$
或
KaTeX parse error: Undefined control sequence: \notag at position 57: …T(\mathbf{y-t})\̲n̲o̲t̲a̲g̲ ̲
其中，$\frac{1}{2}$ 是在不影响能量函数极值点的情况下为了计算的方便而设定的因子。这也是最小二乘法（或称误差平方和函数）的建模思想。针对本部分的例子，可结合下图进行理解

我们可以通过选择使 $E(\mathbf{w})$ 尽可能小的 $\mathbf{w}$ 值来解决曲线拟合问题。由于误差函数是系数 $\mathbf{w}$ 的二次函数，其对系数的导数是关于 $\mathbf{w}$ 的线性函数，因此误差函数的最小化有一个唯一的解 ${\mathbf{w}}^{\ast }$，它可以以闭合形式找到(闭解是指显式解)。这个多项式函数结果可表示为 $y(x,{\mathbf{w}}^{\ast })$.

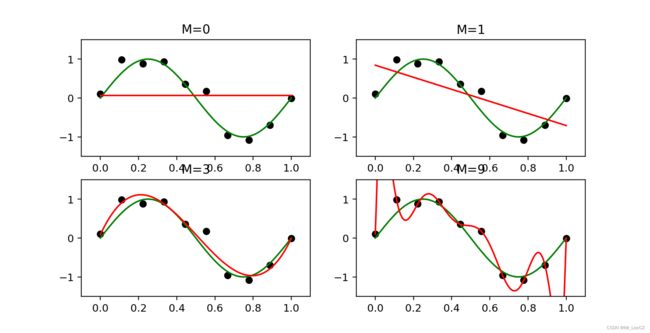
解决曲线拟合问题之后，我们仍然存在选择多项式阶数 $M$ 的问题，称为模型比较或模型选择。下面展示了四个将 $M=0,1,3$ 和 $9$ 阶多项式拟合到给定数据集的结果示例。

#!/usr/bin/python
# -*- coding:utf-8 -*-

#######################################################
# 多项式拟合为例，展示过拟合的例子
# 作者：MR_LeeCZ
#######################################################

import numpy as np
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import Pipeline
import matplotlib.pyplot as plt
from math import pi

# 导入训练集
data = np.load('data/datap4.npy')
x = data[0,:]
t = data[1,:]

# 预处理，把行向量转变为列向量
x.shape = -1, 1 
t.shape = -1, 1

model = Pipeline([('poly', PolynomialFeatures()),
                  ('linear', LinearRegression(fit_intercept=False))])

dims = np.array([0,1,3,9])  # 设定多项式的阶
steps = np.array([1,2,3,4]) # 将图片集合到一张图进行展示，即图的顺序
labels = ['M=0','M=1','M=3','M=9'] # lengend说明

fig = plt.figure(figsize=(12,6),dpi=220) #设置图片的大小和清晰度

for step, dim in zip(steps, dims):
    ax = fig.add_subplot(2,2,step)
    ax.scatter(x, t,c='k') # 画出训练集
    model.set_params(poly__degree=dim)
    model.fit(x, t.ravel())
    x_hat = np.linspace(x.min(), x.max(), num=100) # 测试数据集
    y_true = np.sin(2*pi*x_hat) # 对比的真实结果
    ax.plot(x_hat,y_true,c='g')
    x_hat.shape = -1, 1
    y_hat = model.predict(x_hat)
    ax.plot(x_hat, y_hat,c='r')
    plt.xlim([-0.1,1.1])
    plt.ylim([-1.5,1.5])
    plt.title(labels[step-1])

plt.show()

结果展示图如下，分别对应 $M=1,2,3,9$

从上述的例子可知，结果的好坏取决于两方面：一是多项式对数据点的拟合能力；二是多项式对真实函数的表示能力（微积分上学的泰勒展开式）。我们注意到常数（$M=0$）和一阶（$M=1$）多项式对数据的拟合很差，同时多项式对函数 $sin(2\pi x)$ 的表示也很差。三阶（$M=3$）多项式似乎是示例中函数 $sin(2\pi x)$ 的最佳拟合。当我们进入一个更高阶多项式（$M=9$）时，我们得到了对训练数据的一个极好的拟合（此时的误差为零）。实际上，多项式正好通过每个数据点和 $E(\mathbf{w})=0$. 然而，拟合曲线振荡剧烈，给出了 $sin(2\pi x)$ 函数的一个很差的表示。后一种行为称为过拟合（overfitting）.

3. 拟合效果的评价

如前所述，我们的目标是通过对新数据进行准确预测来实现良好的泛化。我们可以通过考虑一个单独的测试集来定量地了解泛化性能对 $M$ 的依赖性，该测试集包含 $100$ 个数据点，这些数据点的生成过程与用于生成训练集的过程完全相同，但对目标值中包含的随机噪声值有了新的选择。对于 $M$ 的每一个选择，我们可以评估 $E(\mathbf{w})$ 由（1.2）给出的训练数据，我们还可以评估 $E(\mathbf{w})$ 对于测试数据集。我们可以很方面地利用**均方根（Root Mean Square, RMS）**对模型的泛化能力进行评估

KaTeX parse error: Undefined control sequence: \notag at position 36: …athbf{w}^*)/N} \̲n̲o̲t̲a̲g̲ ̲
其中 $N$ 在分母上目的是在相同的基础上比较不同大小的数据集，平方根确保在与目标变量t相同的标度（和相同的单位）上测量的 $E_{RMS}$.

def rmse(a, b):
    return np.sqrt(np.mean(np.square(a - b)))

training_errors = []
test_errors = []

for i in range(10):
    feature = PolynomialFeature(i)
    X_train = feature.transform(x_train)
    X_test = feature.transform(x_test)

    model = LinearRegression()
    model.fit(X_train, y_train)
    y = model.predict(X_test)
    training_errors.append(rmse(model.predict(X_train), y_train))
    test_errors.append(rmse(model.predict(X_test), y_test + np.random.normal(scale=0.25, size=len(y_test))))

plt.plot(training_errors, 'o-', mfc="none", mec="b", ms=10, c="b", label="Training")
plt.plot(test_errors, 'o-', mfc="none", mec="r", ms=10, c="r", label="Test")
plt.legend()
plt.xlabel("degree")
plt.ylabel("RMSE")
plt.show()

结果展示如图

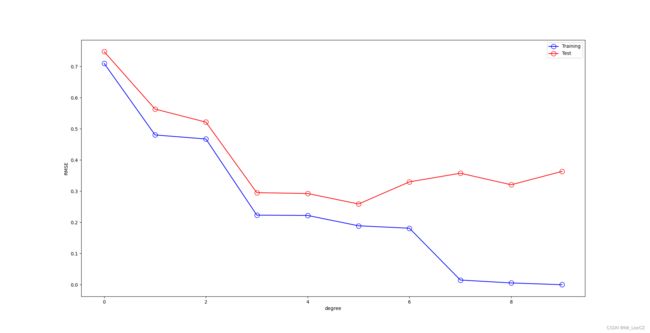
图结果显示了不同 $M$ 值的训练和测试集根均方误差图。测试集误差是衡量我们在预测 $x$ 的新数据观测的 $t$ 值方面做得有多好的一个指标。我们从图中注意到，$M$ 的小值给出了相对较大的测试集误差值，这可以归因于这样一个事实，即相应的多项式是相当不柔软的，且不能捕获函数 $sin(2\pi x)$ 中的振荡。$M$ 的值在3到 8 的范围内给出测试集误差较小，这些值也给出了生成函数 $sin(2\pi x)$ 的合理表示。

对于 $M=9$，训练集误差变为零，正如我们所期望的，因为这个多项式包含 10 个自由度，对应于 10 个系数 $w_0,\cdots ,w_9$，因此可以精确地调整到训练集中的 10 个数据点。然而，测试集误差变得非常大，如图所示，相应的函数 $y(x,\mathbf{w})$ 表现出剧烈的波动。

4. 拟合效果的改进

为了获得较好的效果，就需要根方误差小，且不出现过拟合。出现过拟合的原因是因为模型的复杂度太高，即 $x$ 的阶数过高，也可以理解为 $\mathbf{w}$ 中的非零元素过多。综上，好的拟合效果是小的根方误差和少的特征个数。针对这种分析，通常我们有两种方法可以获得好的拟合效果：一种是增加数据集的规模；而是减少有效特征的个数。

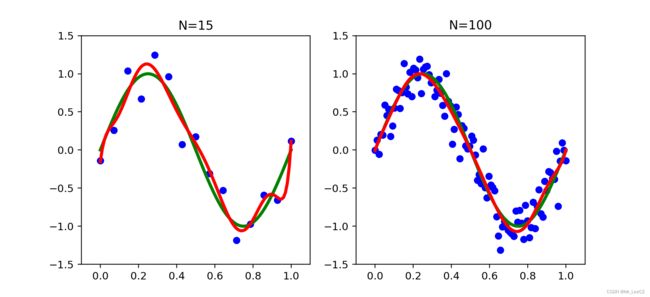
增加数据集的规模是比较简单的一种避免过拟合的方法。但是，这种方法只能获得理论上的优势，因为毕竟数据集的规模是实现固定的，很难在原有基础上进行补充。

#!/usr/bin/python
# -*- coding:utf-8 -*-

#######################################################
# 多项式拟合为例，展示避免过拟合的策略
# 作者：MR_LeeCZ
#######################################################

import numpy as np
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import Pipeline
import matplotlib.pyplot as plt
from math import pi

# 载入较少的数据
data1 = np.load('data/datap9-1.npy')
x1 = data1[0,:]
t1 = data1[1,:]

x1.shape = -1, 1 # 把行向量转变为列向量
t1.shape = -1, 1

# 载入较多的数据
data2 = np.load('data/datap9-2.npy')
x2 = data2[0,:]
t2 = data2[1,:]

x2.shape = -1, 1 # 把行向量转变为列向量
t2.shape = -1, 1


model = Pipeline([('poly', PolynomialFeatures()),
                  ('linear', LinearRegression(fit_intercept=False))])


fig = plt.figure(figsize=(12,4),dpi=220)
# 第一个图
ax1 = fig.add_subplot(1,2,1)
ax1.scatter(x1, t1,marker='o',c='b')
model.set_params(poly__degree=9)
model.fit(x1, t1.ravel())

x_hat1 = np.linspace(x1.min(), x1.max(), num=100)
y_true1 = np.sin(2*pi*x_hat1)
ax1.plot(x_hat1,y_true1,c='g',linewidth=3)

x_hat1.shape = -1, 1
y_hat1 = model.predict(x_hat1)
ax1.plot(x_hat1, y_hat1,c='r',linewidth=3)
plt.xlim([-0.1,1.1])
plt.ylim([-1.5,1.5])
plt.title('N=15')

# 第二个图
ax2 = fig.add_subplot(1,2,2)
ax2.scatter(x2, t2,c='b')
model.set_params(poly__degree=9)
model.fit(x2, t2.ravel())

x_hat2 = np.linspace(x2.min(), x2.max(), num=100)
y_true2 = np.sin(2*pi*x_hat2)
ax2.plot(x_hat2,y_true2,c='g',linewidth=3)

x_hat2.shape = -1, 1
y_hat2 = model.predict(x_hat2)
ax2.plot(x_hat2, y_hat2,c='r',linewidth=3)
plt.xlim([-0.1,1.1])
plt.ylim([-1.5,1.5])
plt.title('N=100')

plt.show()

通常用来控制过拟合现象的一种技术是正则化技术，它是在误差函数（1）中添加惩罚项，以阻止系数达到大值，即

KaTeX parse error: Undefined control sequence: \notag at position 152: …ert_2^2 \leq R \̲n̲o̲t̲a̲g̲ ̲
由拉格朗日乘子法整理得

KaTeX parse error: Undefined control sequence: \notag at position 122: …f{w}}\Vert_2^2 \̲n̲o̲t̲a̲g̲ ̲
其中，$\Vert \mathbf{w}{\Vert }_2^2={\mathbf{w}}^T\mathbf{w}=w_0^2+w_1^2+\cdots +w_M^2$，系数 $\lambda$ 决定正则项相对于平方误差项之和的相对重要性。注意，经常从正则化器中省略系数 $w_0$，因为它的包含会导致结果取决于目标变量的原点选择（Haste等人，2001），或者它可能包含但具有自己的正则化系数。这些技术在统计中称为收缩方法，因为它减少了系数的值。二次正则化的特殊情况称为岭回归（rige-regression）（Hoerl和Kennard，1970）。在神经网络中，这种方法被称为权值衰减。其计算过程中系数的变化和 $\lambda$ 的取值关系可从下表观察

计算的拟合效果可通过python代码实现

#!/usr/bin/python
# -*- coding:utf-8 -*-

import numpy as np
from sklearn.linear_model import Ridge
from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import Pipeline
import matplotlib.pyplot as plt
from math import pi

# 载入较少的数据
data1 = np.load('data/datap9-1.npy')
x1 = data1[0,:]
t1 = data1[1,:]

x1.shape = -1, 1 # 把行向量转变为列向量
t1.shape = -1, 1


model = Pipeline([('poly', PolynomialFeatures()),
                  ('ridge', Ridge(alpha=np.exp(-18)))])

model2 = Pipeline([('poly', PolynomialFeatures()),
                  ('ridge', Ridge(alpha=np.exp(0)))])


fig = plt.figure(figsize=(12,2),dpi=220)
# 第一个图
ax1 = fig.add_subplot(1,2,1)
ax1.scatter(x1, t1,marker='o',c='b')
model.set_params(poly__degree=9)
model.fit(x1, t1.ravel())

x_hat1 = np.linspace(x1.min(), x1.max(), num=100)
y_true1 = np.sin(2*pi*x_hat1)
ax1.plot(x_hat1,y_true1,c='g',linewidth=3)

x_hat1.shape = -1, 1
y_hat1 = model.predict(x_hat1)
ax1.plot(x_hat1, y_hat1,c='r',linewidth=3)
plt.xlim([-0.1,1.1])
plt.ylim([-1.5,1.5])
plt.title('N=15,M=9,alpha=exp(-18)')

# 第二个图
ax1 = fig.add_subplot(1,2,2)
ax1.scatter(x1, t1,marker='o',c='b')
model2.set_params(poly__degree=9)
model2.fit(x1, t1.ravel())

x_hat1 = np.linspace(x1.min(), x1.max(), num=100)
y_true1 = np.sin(2*pi*x_hat1)
ax1.plot(x_hat1,y_true1,c='g',linewidth=3)

x_hat1.shape = -1, 1
y_hat1 = model2.predict(x_hat1)
ax1.plot(x_hat1, y_hat1,c='r',linewidth=3)
plt.xlim([-0.1,1.1])
plt.ylim([-1.5,1.5])
plt.title('N=15,M=9,alpha=1')

plt.show()

实现结果如下

=9)
model2.fit(x1, t1.ravel())

x_hat1 = np.linspace(x1.min(), x1.max(), num=100)
y_true1 = np.sin(2pix_hat1)
ax1.plot(x_hat1,y_true1,c=‘g’,linewidth=3)

x_hat1.shape = -1, 1
y_hat1 = model2.predict(x_hat1)
ax1.plot(x_hat1, y_hat1,c=‘r’,linewidth=3)
plt.xlim([-0.1,1.1])
plt.ylim([-1.5,1.5])
plt.title(‘N=15,M=9,alpha=1’)

plt.show()

实现结果如下
![在这里插入图片描述](https://img-blog.csdnimg.cn/59102c6a6d9d43ddb187d25b852f3bfc.png#pic_center)