【从零开始的机器学习】-03 一元线性回归与代价函数
1. 例子:假设我们有一些房屋的数据,然后想要通过这些数据来估计某栋房子的价格。如果我们决定只使用房屋的面积来预测,如何建立一个预测模型呢?
假设我们的数据是:
| 房屋面积 x( m 2 m^{2} m2) | 房价 y(万元) |
|---|---|
| 130 | 700 |
| 65 | 320 |
| 80 | 392 |
| 95 | 480 |
| 75 | 390 |
| 125 | 654 |
| 45 | 243 |
| 90 | 431 |
| 105 | 591 |
| 73 | 421 |
| 128 | 518 |
| 66 | 281 |
| 85 | 400 |
| 91 | 281 |
| 62 | 325 |
为了更加直观,我们根据房屋的面积和房屋价格绘制了一个散点图,如下:

图中的每个点都代表着一栋房屋,横坐标 x 表示每栋房子的面积,而纵坐标 y 表示这个房子的价格。通过观察,我们发现,房价与房屋面积大约成正比,即房子面积越大,房屋价格越高。如果我们选择用一条直线作为趋势线,就会发现我们的观察是符合大多数情况的。这里的“选择直线”的操作,就是机器学习中的模型选择。对于不同的问题,适合的模型也不同,而机器学习的一大工作就是选择最适合想要解决的问题的模型,然后将模型的参数最优化,使模型与数据能够足够拟合。所谓“拟合”,就是通过模型能够还原真实数据的程度,还原程度越高,拟合的程度也越高,但拟合度高未必是好事,可能会出现“过拟合”的现象;类似的,如果拟合程度过低,则会出现“欠拟合”的现象。关于过拟合和欠拟合,我们会在之后的章节详细阐述发生的原因以及应对方法,这里只需要记住:拟合是对训练数据准确描述的程度,过高过低都不好,即可。
回到例子当中,我们说,选择用直线模型来拟合我们的训练数据,且只有一个自变量(房屋的面积),那么我们可以得出这个直线的函数为一元一次函数(Linear Function of One Variable)。而我们又想用一条直线来预测房屋的价格,所以是一元线性回归问题。我们曾经学过的一元一次函数的表达式为: f ( x ) = k x + b f(x) = kx+b f(x)=kx+b,k表示直线的斜率,b表示截距,但在机器学习中,一元一次函数的常见表达式为: h θ ( x ) = θ 0 + θ 1 x h_\theta(x) = \theta_0+\theta_1x hθ(x)=θ0+θ1x, θ 0 \theta_0 θ0表示截距, θ 1 \theta_1 θ1表示直线的斜率,这样操作是为了方便之后的一些计算。
现在我们有了用来拟合数据的函数,可我们并不确定 θ 0 \theta_0 θ0和 θ 1 \theta_1 θ1 究竟应该设为多少才合适,如果设置的不合适,就无法很好的拟合数据,可能会出现下面图中的情况:
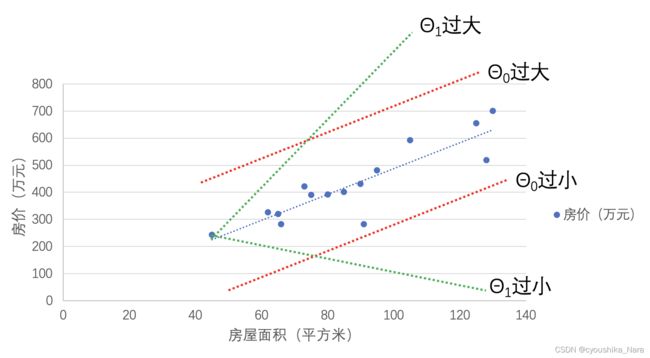
那么怎么办呢?答案:试。只要我们把能取到的 θ \theta θ都试一遍,不就能找到最合适的了吗?那问题又来了, θ \theta θ是实数,有无穷多个,怎么试?况且,数据只有几个或十几个的话,我们还是可以手算的,可要是有成千上万个数据,那就太花时间了。这里就突显出了计算机的优势,计算机最擅长的就是自动地、高效地完成重复劳动(计算),所以我们可以把计算的任务丢给计算机啊,可怎么才能知道设置的 θ \theta θ合不合适呢?这就要用到我们上一章说的代价函数了。
2. 直线模型的代价函数
如我们上一章介绍的那样,代价函数就是计算预测值和真实值之间的差距的函数,差距越小,代价越小,说明模型与训练数据越拟合。而直线模型最常用的代价函数就是平方误差函数(Square Error Function),对于一个一元一次直线函数,其平方误差函数为:
J ( θ 0 , θ 1 ) = ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 2 m J(\theta_0,\theta_1)=\frac{\sum_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})^{2}}{2m} J(θ0,θ1)=2m∑i=1m(hθ(x(i))−y(i))2
- m: 训练数据的个数;
- θ \theta θ:学习算法中的参数
- x ( i ) x^{(i)} x(i):第i个训练数据的输入;
- y ( i ) y^{(i)} y(i):第i个训练数据的预期输出(即正确答案);
- h θ ( x ( i ) ) h_\theta(x^{(i)}) hθ(x(i)):根据函数h,计算第i个训练数据的输入 x ( i ) x^{(i)} x(i)得到的预测结果;
平方误差函数计算的,其实是预测数据与真实数据两点之间的距离。二维坐标中,两点之间的距离D为:
D = ( x 1 − x 2 ) 2 + ( y 1 − y 2 ) 2 D= \sqrt{(x_1-x_2)^{2}+(y_1-y_2)^2} D=(x1−x2)2+(y1−y2)2
而因为函数h是根据x计算出h(x)的,因此两个点的横坐标是相同的,因此 x 1 − x 2 = 0 x_1-x_2=0 x1−x2=0。如果我们再把D取平方,把根号去掉,那么就得到了:
D 2 = ( y 1 − y 2 ) 2 D^{2} = (y_1-y_2)^2 D2=(y1−y2)2
这里,我们将 y 1 y_1 y1替换成预测值 h θ ( x ) h_\theta(x) hθ(x),将 y 2 y_2 y2替换成真实值 y y y,则有: D 2 = ( h θ ( x ) − y ) 2 D^{2} = (h_\theta(x)-y)^2 D2=(hθ(x)−y)2。用图像来表示D的话,就如下图中绿色的线段,每个数据点到同横坐标下的预测值点的距离。

当我们得到了所有预测值和真实值之间的距离的平方后,我们将其加起来,取平均数,就能知道当前的直线与真实数据之间的平均距离,就得到了平方误差函数的表达式:
J ( θ 0 , θ 1 ) = ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 2 m J(\theta_0,\theta_1)=\frac{\sum_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})^{2}}{2m} J(θ0,θ1)=2m∑i=1m(hθ(x(i))−y(i))2
也许你会问,为什么是2m,而不是m呢?这是因为,在后序的优化参数的过程中,我们会对函数进行求导,为了简化计算,我们多除以一个2,这样就能在求导时把分子的指数2约分掉。
3. 代码实现:
import random
def h(x,theta0,theta1)->float: #预测函数h
return theta0+theta1*x
def square_error(data,theta0,theta1):
x = data[0] #横坐标
y = data[1] #真实值
total = 0 #总和
m = len(x) #训练数据长度
for i in range(0,m):
total+=pow(h(x[i],theta0,theta1)-y[i],2) #计算误差平方和
print(total/(2*m)) #输出代价
if __name__ == '__main__':
data = [[130,65,80,95,75,125,45,90,105,73,128,66,85,91,62],
[700,320,392,480,390,654,243,431,591,421,518,281,400,281,325]]
theta0 = random.randrange(-10, 10, 1)
theta1 = random.randrange(-10, 10, 1)
square_error(data,theta0,theta1)
4. 预告
好了,我们现在知道怎么去评估一个直线模型的拟合程度了,那我们如何根据评估的结果对参数进行调整呢?
答:梯度下降法(gradient descent)。
下一节,我们将讲解如何梯度下降法的原理以及如何使用梯度下降法来调整参数。