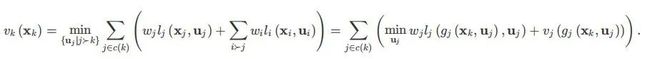“现在的自动驾驶太保守!”看看轻舟智航联合创始人大方这篇论文怎么说
交流群 | 进“传感器群/滑板底盘群”请加微信号:xsh041388
交流群 | 进“汽车基础软件群”请加微信号:ckc1087
备注信息:群名称 + 真实姓名、公司、岗位
Comprehensive Reactive Safety: No Need For A Trajectory If Y ou Have A Strategy
论文地址:https://arxiv.org/abs/2207.00198
【写在前面】
当前,为保证自动驾驶运动规划的安全性,常采用可达性分析及类似方法,对道路上的所有物体(如道路上的人类驾驶车辆)行为采取保守约束,确保车辆在道路环境上不会发生任何碰撞。
本文作者指出,由于道路情况会随时间而变化,自动驾驶车辆所做决策也应随未来道路情况进行变化,因此严格规避整个可达区域的规划轨迹是不必要的,而且忽视这种应对未来道路变化的反应能力,将使其所做决策过于保守,从而丧失灵活性。
基于此动机,作者提出一种新的安全框架来融合自动驾驶汽车对未来环境变化的反应。最后,作者在多个城市驾驶场景(如无保护的左转和车道合并等)进行了模拟实验,证明了本文所提出 Reactive ILQR 规划算法具备更优的灵活性和安全性。
1. 文章动机
自动驾驶是被公认可显著改善人类生活的技术之一,安全性是其核心问题。事实上,智能驾驶员相比人类在预见和避免碰撞方面具有明显优势,一方面智能驾驶员在求解微分方程和计算几何交叉点方面优势明显,另一方面不会产生疲惫和走神等问题。已有大量工作(比如以可达性分析为工具)可以规划安全轨迹或者判定轨迹的安全性,但常以车辆轨迹与障碍物所占时空区域不相交作为安全验证规则,该思路虽便于理论分析,却在真实自动驾驶解决方案中并不实用。
现有基于可达性分析的方法最大问题之一在于规划过于保守,以至于很多时候这种安全分析的结果是自动驾驶车辆在路上寸步难行。上图展示了一种常见驾驶场景,即自动驾驶汽车A车试图超越相邻车道上的慢速车辆B。
由于A车事先并不知道B车是否有变道意图,从而B车的在未来几秒内的可达集涵盖了两条车道,导致A车无法做出超车决策。而且,B车的加速度未知,所以它有可能出现在车道内的任何纵向位置上,因此B车的可达集将覆盖A车前方的整个时空区域。
为避免与B车可达集产生交叉点,A车必须制动并在B车的后方进行跟随。虽然A车基于可达性分析制定的策略是安全的,但相对保守。
严格的不相交虽可以保证A车的绝对安全,但却限制了其行车效率,这是完全不必要的。事实上,一个动态对象的可达集会随着时间变得无限大,如基于现有的规划策略,将导致A车无法正常行驶。
然而,根据人类驾驶员的经验可知,B车是无法同时占有两条车道,无论占有哪条,另一条都将会开放,因此A车总是会有安全超车的机会。虽然这个结论对于人类驾驶员来说显而易见,但在目前的自动驾驶安全框架中并未得到实现。
这里的关键见解是,在正常驾驶中,规划器生成的轨迹几乎从未完全按原样执行。现代城市自动驾驶系统通常以 10Hz 左右的频率运行,并且轨迹(通常具有 10 秒或更长时间的时域)是以流水线的方式规划和执行的,因此每个轨迹只有初始100毫秒部分(约百分之一)会被控制器执行,之后控制器就会接收到并转而执行下一个轨迹了。
新轨迹通过结合最新的传感器数据来响应环境的变化,因此通常会略有不同,除非旧轨迹中使用的运动预测是完全确定性和准确的。既然AV到达轨迹的后半部分的时候,它应该会掌握更多周围环境的信息,也应该能够找到更好的应对,那么就算AV当前掌握的有限信息不足以保证在这种未来时刻的安全,也没什么大不了的。
轨迹的后半部分不会由车辆执行,因此严格检查这部分轨迹上的碰撞不会有利于自动驾驶系统的整体安全性。这意味着,应该重新考虑“确保整个轨迹上会与任何障碍物的任何潜在运动发⽣碰撞”这个原则,这是已知的所有自动驾驶安全框架普遍采用的范式。我们需要的是一个新的安全框架,它考虑到未来轨迹将如何响应环境变化而变化,并确保反应是安全的,而不是确保当前轨迹是安全的。
因此,新的安全框架需要考虑未来轨迹受环境的影响,而不仅仅是针对当前轨迹进行决策。本文作者提出了综合反应安全这一概念,来确保自动驾驶系统可以通过新得到的观察做出反应来避免碰撞,而非从开始就要求其设计一条完全不可能发生碰撞的轨迹。
这将使得系统在面对不同的未来场景时,可以给出灵活的执行策略,只要保证在响应前有足够的时间来观察环境并确认场景。当传统策略不存在安全轨迹方案时,本文方法将带来更自由且安全的行车方案。换言之,在综合反应安全框架下,自动驾驶系统给出的并非轨迹方案,而是策略,即给定状态返回合理的动作。
本文的主要贡献如下:
1)本文提出综合反应安全框架,首次阐述如何自动驾驶车辆该对未来环境变化做出即时反应。该框架极大提升了规划的灵活性,在面对挑战性场景时,使得传统可达性分析方法具有新的可能性。同时本文证明,限制更少的综合反应安全条件仍能保证车辆的安全运行。
2)本文提出反应式 ILQR (Reactive ILQR, RILQR)算法,即一种满足综合反应安全条件的实用规划算法。通过在城市驾驶中常见的四种代表性场景中进行比较,证明所提出的 RILQR 规划器在与其他车辆交互时不但更安全,而且更灵活,有能力以基于传统可达性分析的规划算法无法实现的新方式进行互动。
2. 相关工作
2.1. 安全性
安全性通常被定义为自动驾驶车辆的轨迹和障碍物之间不存在碰撞的条件,包括考虑两者的不确定性。规划器通过以下两类思路确保所产生轨迹的安全性:要么通过将安全性作为硬约束进行轨迹优化,要么对更宽松的碰撞约束所得轨迹进行安全验证,并在发现碰撞后回滚到最后验证的状态,改用安全的备选轨迹,或执行纠正指令以恢复安全。
约束优化算法在数值优化领域中得到了广泛的研究。大量的 优化技术也被应用于自动驾驶中的运动规划任务,比如:顺序二次规划 (SQP) 、线性规划 (LP) 和混合整数二次规划 (MIQP) 。其中,约束ILQR是迭代线性二次调节器 (ILQR)的扩展,以支持使用障碍函数的任意状态作为约束条件,也可用于强制执行安全约束。作者在受约束的ILQR之上构建了本文的方法实现。
2.2. 不确定性的来源
在现实世界中运行的自动驾驶系统面临着许多可能与安全相关的不确定性来源,它们已成为许多研究的主题。噪声控制和环境干扰可以通过反馈控制来限制,从而将自动驾驶车辆轨迹扩展为控制器可以确保永不离开的不变集。
测量(定位和感知)噪声通常通过用缓冲区扩充安全约束来处理。由于传感器限制(例如遮挡)导致自动驾驶车辆对环境了解的不确定性可以通过在遮挡区域产生虚拟障碍来解决。
对于车辆等动态障碍物,其未知的未来运动和意图是不确定性的重要来源,对此使用可达性分析的保守估计技术,以及大量研究关于数据驱动的运动预测技术。
Li等人通过离线的聚类方法产生一系列对象行为类别,在线上对物体行为进行分类来限制可达集。本文和上述工作有共同的出发点,但不依赖会失去安全保证的数据驱动方法,并且仅通过观察到的物体运动的证据排除可达集的部分。
2.3. 可达性
可达性分析是研究动力系统的工具。一些技术将该过程表述为微分博弈并求解其 Hamilton-Jacobi PDE方程,而另一些技术则使用保守线性化来近似非线性动力学。在自动驾驶应用中,可达性分析用于计算在某些运动学、动力学或行为假设下,由于未知意图和行为,物体可能到达的空间位置的保守超集。
有些研究采用关于物体行为的假设来抑制可达集的增长,常见的方法是把交通法规形式化;这样的规划器需要处理的可达集会比较小,但不能保证不发生碰撞,而只能保证在发生碰撞时,自身没有过错(不承担责任)。
虽然在某些情况下它可能有助于防止可达集阻塞车辆,但该研究方向的最新技术通常仅限于围绕驾驶方向约束和安全距离的简单规则集,难以处理复杂性现实世界的交通。人类交通规则的解释和形式化是一项看起来要困难得多的任务。
另一种削减可达集的方法是降低规划时域。然而,依靠调整时域来控制可达性会使规划器变得脆弱,并且当时域趋于无穷大时,缺乏对期望行为的收敛性在理论上是不能令人满意的。本文提出的安全框架不是可达性分析的替代品,而是一种更灵活的应用方式,旨在解决其保守性的弱点。它可以与任何计算可达集的现有技术一起使用。
值得指出的是,尽管围绕所有可达集进行规划是不必要的保守,因为未来的新观察将实现更有针对性的响应,但在自动驾驶系统完成规划后遭受严重故障并失去感知能力的最坏情况下,这种响应就实现不了了。虽然这种情况很少见,但却是不容忽视的风险。
在这种情况下,将无法执行需要观察更新的计划,并且只能绕过所有当前已知的可达集的开环轨迹来实现安全性。但这很可能是不可行的。在设计安全的自动驾驶系统时,必须包括回退机制,以使车辆在此类危险情况下回到最低安全状态,可能涉及可达性分析。然而,在最坏情况下能力的下降不应该束缚我们在一般情况下追求更高标准的驾驶能力。本文提出的CRS框架正是朝这个方向努力。
3. 方法
3.1. 综合反应安全
令自动驾驶系统最新的感知预测点作为制定驾驶计划的初始时刻t = 0。令 T 表示规划时间域 [0,tend],X 表示空间域(通常是地面上的 2D 空间)。一条轨迹表示为一个函数τ:T→X,所有轨迹的集合用 T={τ∣τ:T→X}表示。给定轨迹τ,使用Cτ来表示相应的扫描体积轨迹Cτ:T→P(X)使得Cτ(t)是 t 时刻车辆的碰撞体积。
给定感知子系统报告的一组对象 O,预测子系统将每个对象i∈O 的潜在运动范围预测为一组轨迹Pi⊆T 。这个集合也可以看作是对象的时空可达集。此外,交互感知预测器将能够给出单个对象运动的可能组合,作者称之为未来(futures),具体定义为:F={(p1,p2,…,pN)∣pi∈Pi}⊆P1×P2×…×PN,描述了未来所有可能展开方式。
作者使用下标符号来标识特定对象在未来的轨迹:对于f∈F ,fi∈Pi是对象 i 将在未来实现的轨迹。
规划子系统负责制定驾驶计划。给定生成轨迹 τ∈T,传统的安全性准则要求其与任何预测都没有冲突:Cτ(t)∩Cp(t)=∅,∀p∈Pi,∀i∈O,∀t∈T。这个条件可以等价地写成:Cτ(t)∩Cfi(t)=∅,∀i∈O,∀f∈F,∀t∈T。
本文考虑对未来可能发生的任何事情做出反应来确保安全的原则,提出规划器应制定一个策略,将潜在的未来情况映射到轨迹上,即σ:F→T。换言之,规划子系统为每个未来场景规划了一条轨迹。
为确保自动驾驶系统遵循该策略,要求其必须满足一定因果约束:轨迹必须在未来变化发生后对其进行“反应”。例如,不应该在车辆显示出准备切入的迹象之前开始变道。
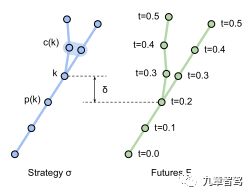
定义 1(要求 I:反应因果关系):如果对于任何两个未来 f,g∈F和任何时间t∈T,只要fi(t′)=gi(t′),∀i∈O,∀t′∈[0,t−δ],其中 δ 是传感延迟,条件σ(f)(t)=σ(g)(t)就成立。
这里,传感延迟δ是环境中发生变化时间点和自动驾驶系统完成识别时间点之间的延迟。要求I指出,如果一个策略对具有不同轨迹的两个未来(Future)做出响应,则轨迹之间的差异不应早于两个未来分歧的时间加上感知延迟δ,这是自动驾驶系统能够区分两种未来并做出相应反应的最早时间。
定义 2(要求 II:反应安全):如果条件Cσ(f)(t)∩Cfi(t)=∅对于所有f∈F,、所有时间 t∈T和所有对象i∈O 都成立,则策略σ满足反应安全要求。
请注意,这里要求II明显弱于传统的安全条件 Cτ(t)∩Cfi(t)=∅,因为前者只要求每个轨迹与其对应的未来没有碰撞,而不是与所有可能的未来。这是允许自动驾驶系统在可达集变得过于分散时避免卡住的关键区别:每种情况都可以有自己的特定解决方案,并且针对一种情况的解决方案不需要关注处理其他情况。
基于以上两个要求的定义,可以给出本文定义的反应安全条件,称为综合反应安全 (CRS),具体如下:
定义 3(综合反应性安全,CRS):
如果策略σ同时满足要求I和II,则称其满足CRS条件。通过定理1,证明采用CRS策略是可保证行驶安全的。
定理1(按照CRS策略的反应性驾驶策略是安全的):考虑一个自动驾驶系统,该系统配备了在时间0时满足CRS的策略σ。在任何未来时间t∈T ,系统将观察到每个物体在[0,t−δ]时间范围内的运动;对于每个物体i∈O,到某个未来时刻为止的运动可表示为mi:[0,t−δ]→X 。只要系统执行的是任意一个与观察到的运动相兼容的未来f∈F所对应的轨迹 σ(f)(即f 满足fi(t′)=mi(t′),∀t′∈[0,t−δ],∀i∈O),那么该系统就会避免与任何物体发生碰撞。
一旦规划器通过CRS成功完成规划,就一定存在一个避免碰撞的方法,即使它没有指定控制器要遵循的特定轨迹。只要自动驾驶系统不断观察环境并及时执行相应的反应,它就不会发生碰撞,同时可以享受传统方法没有的自由度。
证明:在F中所有可能的未来中,有一个未来将是最终在现实中发生的,称为f∗。根据要求 II,如果系统在 T 上执行σ(f∗),则不会发生碰撞。根据定义,在任何时间 t∈T,所有跟观察到的运动mi相兼容的未来 f(包括f∗)的时间t−δ以前的部分都是相同的。根据要求 I,他们对应的策略 σ(f)(包括 σ(f∗)),在时间t之前的部分都是相同的。因此,在时间区间T内,执行 σ(f∗)等价于对任何兼容的f执行σ(f),而这正是系统所做的。
一旦规划器通过 CRS 成功规划或验证策略,它就有一个避免碰撞的方法,即使它没有指定控制器要遵循的特定轨迹。只要 A V 不断观察环境并及时执行相应的反应,它就不会发生碰撞,同时享受传统基于轨迹的框架所不具备的额外自由度。
3.2. Reactive ILQR
本节中,根据上节提出的综合反应性安全CRS,作者基于经典的ILQR(Iterative Linear Quadratic Regulator)算法框架提出了Reactive ILQR,该算法输出的是符合CRS的策略,而非轨迹。由于用策略规划器代替轨迹规划器还处于早期探索,作者将尽量保持预测和决策等支持组件简单化。
1) Strategy as a tree of trajectories(策略作为轨迹树):
要求I规定策略中的所有轨迹共享一些前缀,前缀长度取决于所对应未来分叉的时间先后。这表明可将策略表示为轨迹树,深度方向为时间。在时间t之前共享前缀的两条轨迹被存储为一棵树,其中树干对应于时间[0,t]的公共前缀段,并且随着时间 (t,tend ] 的两个不同的后缀段对应的两个分支。类似地,未来F也可被表示为一棵树。
2) Strategy branching according to future branching(根据未来分支的策略分支):
由于每个未来 f 允许策略的轨迹σ(f)不同,因此策略应该在未来分支时分支,换言之,策略树应该与未来树具有相同的拓扑结构。根据要求 I,策略树上的分支点不得早于未来树上的对应点加上δ,但可以晚于该点,因为某些情况不需要立即做出反应。为简单起见,作者在每个未来分支点之后的时间δ处对策略进行简单的分支,如上图所示。
3) Strategy optimization by Reactive ILQR(通过 Reactive ILQR 进行策略优化):
一旦获得策略树的拓扑结构,就可以对其进行离散化和变分优化,同时需遵守要求II提出的安全约束。作者以固定的时间步长Δt(例如,0.1s)将策略树时间离散化为符号k引用的多个点。与原始 ILQR 中的步长索引不同,这里的k是策略树中一个点的标识符,每个点的时间t(k)不一定唯一,因为来自同一父级的多个分支具有相同的时间值。根是唯一时间为 0 的点:t(root)=0。每个点 k(根除外)总是有一个唯一的父点 p(k),这是它的前一步:t(k)=t(p(k))+Δt。每个点 k(除了末端的叶子点)还有一个或多个子点 c(k)={j∣p(j)=k},它们是它的下一步:t(j)=t(k)+Δt,∀j∈c(k)。偏序 ≺ 可以自然地定义为从根开始在同一路径上的点;例如,如果 k 是 j 的祖先,则k≺j。大多数点都只有一个孩子,因为分支很少发生。分支点将树分割成多个线性块,每个块都是包含多个点的轨迹段,最后一个具有多个指向后续分支块的子节点。将 ILQR 算法扩展为使用这种树形拓扑即为本文提出的Reactive ILQR 新算法。
单独考虑时,每个段只是一个线性轨迹序列,可以直接应用 ILQR。唯一棘手的问题是后向传播中的值函数参数(例如梯度和 Hessians)以及前向传播中的最佳状态和控制需要在时间相邻轨迹段相遇的分支点上传播。具体来说,给定自动驾驶系统状态转移函数gk和应用程序指定的代价函数lκ(可能随k变化),策略树σ上的最优控制u∗(和相关状态 x∗)由以下优化给出:
其中 X0 是当前的 A V 状态,hk是执行要求 II的碰撞约束,wk是一个权重因子,用于归一化兄弟分支之间的贡献,其中 wk=∑i∈c(k)wi。可以将这些权重视为使解决方案偏向某些结果的概率;为简单起见,作者通过设置wk=1|c(p(k))|ωp(k)和 wroot =1将权重均匀分布在每个分支点的所有兄弟分支上。
树拓扑上 k 点的(负)价值函数vk也称为 cost-to-go 函数由下式给出:
使用以下递归(贝尔曼方程):
LQR 通过其 Hessian 和梯度以二次形式逼近价值函数。这完成了 ILQR 到树形拓扑的扩展。一般来说,策略树中的每个分支都会使分支点之后要优化的变量数量增加一倍,因此 Y 形策略的计算成本将是线性轨迹的 1 倍到 2 倍。更多的分支会进一步增加计算成本,但在绝大多数城市驾驶场景中,直接关注的对象不超过一个,因此策略树的 ILQR 求解器仍然是高效的。
Reactive ILQR 的最后一个成分是碰撞约束hk。对于每个点 k,其约束 hk只需排除与该点对应的未来的碰撞:
其中算子 d 计算 AV 与物体的碰撞体积之间的欧几里得距离,ϕ(k)={f∣f∈F,k∈σ(f)}是点 k 对应的未来集合,可以策略树是根据未来树的结构构建的。一旦构建,约束 hk 可以在优化问题中使用约束 ILQR 等方法强制执行。
4.实验
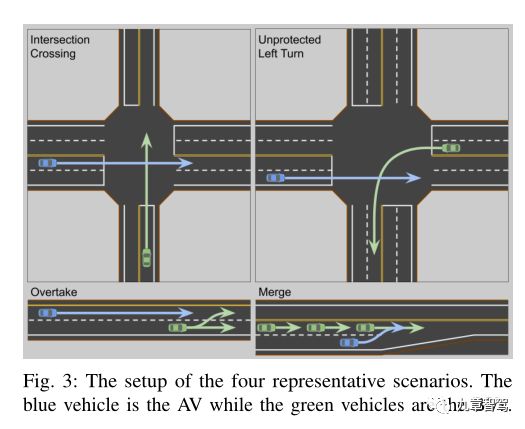
上图描述的场景存在无数种变化,手动设计相关参数,例如交互车辆的初始位置和它们采取的动作(例如是否刹车)。对于每个场景,作者在场景变化空间中的 100 个样本上同时运行 RILQR 和基线 CILQR,并比较汇总统计数据以评估它们在保持安全和取得进展方面的能力。对于交叉和无保护转弯场景,将 100 个样本的batch实验重复 10 次以获得统计上的误差线。
4.1. 十字路口
交叉路口场景需要自动驾驶系统考虑其他车辆(称为背景车辆,BV)的多种可能动作交互。上表展示了本文方法和baseline的结果对比。从上表(左)的结果中可以看出,对AV和BV的初始纵向位置和初始速度变化进行采样的模拟实验证明了:虽然RILQR和基线都确保不会发生碰撞,但由RILQR驱动的AV能够更频繁地通过BV。
上图显示了 RILQR 在典型变化中的行为。
4.2. 无保护左转
当 BV 来自相反方向并打算进行无保护的左转时,也会出现类似的情况。上表(右)的结果展示了本文的方法确实也优于baseline。
上图展示了无保护左转场景变化中的 RILQR 策略。
4.3. 在多车道道路上超车
作者设计了一个场景,其中 BV 在右侧车道上以 1m/s 的缓慢速度移动,可能会在随机时刻向左侧发起车道变换,前提是 AV 不会立即通过它。上表的实验表明,baseline规划器总是无法按预期超车,而 RILQR 在没有任何碰撞的情况下 100% 成功。
上图展示了超车场景变化中的 RILQR 策略。
4.4. 并道
为了在复杂的交互情况下对 RILQR 进行压力测试,作者设置了一个合并挑战场景,其中 AV 接近车道并入左侧车道,连续交通紧密间隔的 BV,每个以 10m/s 的速度行驶(等于 AV 的默认值)初始速度和目标速度),并且可以在到达合并点之前制动或保持速度,就像在交叉场景中一样。除了每个 BV 的单独制动动作外,AV 初始速度和纵向位置也有所不同,以涵盖所有可能的初始配置。上表的结果表明,RILQR 和baseline都遇到了冲突,但 RILQR 确实实现了较低的冲突率。
上图展示了并道场景下的 RILQR 策略。
5. 总结
作者考虑转变当前自动驾驶运动规划中的安全原则,不将安全条件建立在已知环境的静态知识上,而是考虑未来环境将如何变化以及自动驾驶系统将如何反应来重新定义安全性。新的安全性原则,要求规划器架构发生转变,即从规划轨迹到规划策略。为此,作者在提出一种新的安全框架,称为 CRS,并提出一种可行的求解算法RILQR,通过多种驾驶场景的模拟实验,验证了所提框架和算法的有效性。
写在最后
关于投稿
如果您有兴趣给《九章智驾》投稿(“知识积累整理”类型文章),请扫描右方二维码,添加工作人员微信。
注:加微信时务必备注您的真实姓名、公司、现岗位
以及意向岗位等信息,谢谢!
“知识积累”类稿件质量要求:
A:信息密度高于绝大多数券商的绝大多数报告,不低于《九章智驾》的平均水平;
B:信息要高度稀缺,需要80%以上的信息是在其他媒体上看不到的,如果基于公开信息,需有特别牛逼的独家观点才行。多谢理解与支持。
推荐阅读:
◆九章 - 2021年度文章大合集
◆当候选人说“看好自动驾驶产业的前景”时,我会心存警惕——九章智驾创业一周年回顾(上)
◆数据收集得不够多、算法迭代得不够快,就“没人喜欢我”————九章智驾创业一周年回顾(下)
◆详解嬴彻自动驾驶卡车量产技术方法论
◆激光雷达:905与1550的战争
◆单SoC芯片方案,或将加速行泊一体方案规模化量产应用
◆从AVP的实际表现看“L3”自动驾驶商业化的可能性