数模学习（模糊数学篇）——模糊识别（python实现）

目录

一、储备知识

1.课本定义：

2.通俗理解：

 ① 引入小例

 ② 如何识别

二、模糊识别方法

1.最大隶属度原则

        ① 计算方法

        ② 使用方向

2.择近原则

        ① 择近度计算方法和使用方向

三、模糊识别例题

例题1——湖泊水质识别

1. 指标库标准化和样品库标准化：

2.计算各个样本对应各个模式的贴近度：

例题2——土壤质量识别

四、总结​​​​​​​

---

一、储备知识

1.课本定义：

模糊识别属于判别一个对象属于哪个模式的问题，进行模糊识别需要两个条件：

① 事先已知若干标准模式，称作标准模式库；

② 有待识别的对象；

2.通俗理解：

就是判断一个样本属于什么类别的问题啦（诸如汽车牌照识别、空气污染等级识别、土壤质量识别、生态环境识别、湖泊水质识别等）

 ① 引入小例

比如：有一个评价体系有五个标准以及若干评价指标

指标\等级	极好	好	一般	差	极差
指标A	5	4	3	2	1
指标B	5	4	3	2	1

        还有一个样本u，指标A的评分是3.5分，指标B的评分是5分，当然肯定还存在其他评价指标，此处就以“……”略过了。向量形式就是  U={3.5 5 …… }，那么模糊识别就是判断样本u属于这个评价体系中的哪一个等级（极好、好……）。

        那为什么称其为模糊呢？其实也很简单，就是因为这个评价指标是模糊不清的。以指标A为例，假设它的评分范围是[0,6]中的任何实数，那4.5分是什么等级，4.3分呢？1.5分呢？那么这个时候也不能拍脑袋说4.3分，介于好和一般之间，更偏向于一般，所以一般。逻辑上确实没问题，但是如果再加一个指标B是4.6分呢？再加一个呢？就很难很准确的凭借感觉来判断了。

        所以就有了模糊识别这么一个伟大的数学创造。那肯定想问，在指标很多的情况下又如何去精准识别呢？

   ② 如何识别

        现在这里说通俗点的，就是看谁更靠近谁、谁更属于谁（有点舔狗那味儿） ，就是通过一种手段来拟合这种靠近程度、涵纳程度。具体的也没办法用很通俗的话讲清楚。那就直接上硬货吧。

二、模糊识别方法

1.最大隶属度原则

       “ （直接抽象一些，n维，即n个待识别对象）”

        根据定义，此处有m个标准模式，然后有n个待识别对象。则A(xi)=max{A(x1),A(x2)……}，即该识别对象为xi模式（通俗点就是把一个识别对象n1，和m和标准模式进行核算隶属度，然后隶属度最大的便是该对象所处的模式中）

        ① 计算方法

        构建隶属函数。这里不再赘述了，因为CSDN上有很多隶属函数构建方法的讲解。笔者一般喜欢用下列三种：

                                                        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​                ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​​​​​​​​

        其中式1适用于指标越大越好的情况；式3适用于指标越小越好的情况；式2则折中。一个模式中的隶属度可能存在多种函数的参与计算。

          ② 使用方向

        计算标准指标库的隶属度矩阵；计算样品指标库的隶属度矩阵

        Python代码实现为：

import math as m

def lsd(a,minx): #计算隶属度函数
    b=[]
    c=[]
    for i in range(0,len(a)):
            b=a[i]
            for j in range(0,len(b)):
                if j!=2 and j!=1:
                    if b[j]<=minx[j]:
                        c.append(1)
                    elif b[j]>minx[j]:
                        c.append(round(m.exp(-((b[j]-minx[j])**2)),4))
                elif j==2:
                    if b[j]<=minx[j]:
                        c.append(0)
                    elif b[j]>minx[j]:
                        c.append(round(1-m.exp(-((b[j]-minx[j])**2)),4))
                else:
                    if b[j]<0.09:
                        c.append(round(m.exp(-((b[j]-0.09)**2)),4))
                    elif b[j]>0.09:
                        c.append(round(1-m.exp(-((b[j]-0.09)**2)),4))
                    else:
                        c.append(1)
    return c

def main():
    s=[] #输入标准库指标，一个模式是一个行向量输入
    t=[] #输入样品库指标，一个模式是一个行向量输入
    miny=[] #输入每个指标的最小值
    print(lsd(s,miny))
    print(lsd(t,miny))

if __name__ == "__main__":
    main()

2.择近原则

       择近原则衡量的是两个集合之间的贴近程度，通常是用σ(A,B)来表达。贴近度越大则表明两个模糊集越相近，越相似。（不知道理解的对不对，经管专业的话，其实可以拿OLS的原理来思考这个问题）

        ① 择近度计算方法和使用方向

        择近度计算方法有很多，常见的如格贴近度、最小最大贴近度、最小平均贴近度、海明贴近度、欧几里得贴近度等。此处重点介绍最小最大贴近度。通过计算每一个样本对每一个模式的贴近度，再根据择近原则选定越接近的那个模式，则成为该样品的模式。

        Python代码实现：

import numpy as np

def minMaxDist(x,y):
    x = np.array(x,np.float16).reshape(-1)
    y = np.array(y,np.float16).reshape(-1)
    map_xy = np.vstack((x,y))
    return np.sum(np.min(map_xy,axis=0))/np.sum(np.max(map_xy,axis=0))

def main():
    s=[] #输入标准库指标，一个模式是一个行向量输入
    t=[] #输入样品库指标，一个模式是一个行向量输入
    miny=[] #输入每个指标的最小值

    # 最小最大值评价度量
    thd1=[]
    for i in range(0,3):
        p=lsd(t,miny)[0+i*4:4+i*4]
        for j in range(0,5):
            q=lsd(s,miny)[0+j*4:4+j*4]
            thd1.append(minMaxDist(p,q))
    for m in range(0,3):
        print(thd1[0+5*m:5+5*m])#输出每个样本的贴近度

if __name__ == "__main__":
    main()

注意：此处并没有加入lsd函数，因此在调用时记得补上lsd函数。

三、模糊识别例题

例题1——湖泊水质识别

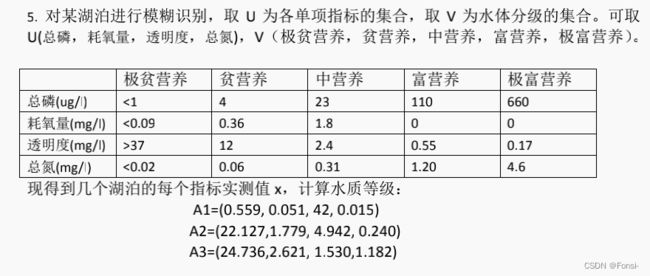
        可以发现，总磷、总氮指标是越低越好；耗氧量是居中为佳；透明度为越高越好。可能有人会有疑问怎么定义这个好，其实可以看等级水平：极贫营养的湖泊一般来说对人直接饮用或使用是最方便、健康以及无害的。因此从人类实用主义角度出发认为极贫营养是最好的，那么指标就是一一对应的关系了。由于笔者是文科生，只知道富营养化不好，如果上述逻辑有误，请读者予以斧正！

        1. 指标库标准化和样品库标准化：

import math as m

def lsd(a,minx):
    b=[]
    c=[]
    for i in range(0,len(a)):
            b=a[i]
            for j in range(0,len(b)):
                if j!=2 and j!=1:
                    if b[j]<=minx[j]:
                        c.append(1)
                    elif b[j]>minx[j]:
                        c.append(round(m.exp(-((b[j]-minx[j])**2)),4))
                elif j==2:
                    if b[j]<=minx[j]:
                        c.append(0)
                    elif b[j]>minx[j]:
                        c.append(round(1-m.exp(-((b[j]-minx[j])**2)),4))
                else:
                    if b[j]<0.09:
                        c.append(round(m.exp(-((b[j]-0.09)**2)),4))
                    elif b[j]>0.09:
                        c.append(round(1-m.exp(-((b[j]-0.09)**2)),4))
                    else:
                        c.append(1)
    return c

def main():
    s=[[1,0.09,37,0.02],
       [4,0.36,12,0.06],
       [23,1.8,2.4,0.31],
       [110,0,0.55,1.20],
       [660,0,0.17,4.6]]
    t=[[0.559,0.051,42,0.015],
       [22.127,1.779,4.942,0.240],
       [24.736,2.621,1.530,1.182]]
    miny=[1,0,0.17,0.02]
    print(lsd(s,miny))
    print(lsd(t,miny))

if __name__ == "__main__":
    main()

得到标准库的隶属度矩阵如下：

1	1	1.0	1
0.0001	0.0703	1.0	0.9984
0.0	0.9463	0.9931	0.9193
0.0	0.9919	0.1345	0.2485
0.0	0.9919	0	0.0

得到样品库的隶属度矩阵如下：

1	0.9985	1.0	1
0.0	0.9423	1.0	0.9528
0.0	0.9983	0.8427	0.2592

2.计算各个样本对应各个模式的贴近度：

import numpy as np
import math as m

def lsd(a,minx):
    b=[]
    c=[]
    for i in range(0,len(a)):
            b=a[i]
            for j in range(0,len(b)):
                if j!=2 and j!=1:
                    if b[j]<=minx[j]:
                        c.append(1)
                    elif b[j]>minx[j]:
                        c.append(round(m.exp(-((b[j]-minx[j])**2)),4))
                elif j==2:
                    if b[j]<=minx[j]:
                        c.append(0)
                    elif b[j]>minx[j]:
                        c.append(round(1-m.exp(-((b[j]-minx[j])**2)),4))
                else:
                    if b[j]<0.09:
                        c.append(round(m.exp(-((b[j]-0.09)**2)),4))
                    elif b[j]>0.09:
                        c.append(round(1-m.exp(-((b[j]-0.09)**2)),4))
                    else:
                        c.append(1)
    return c

def minMaxDist(x,y):
    x = np.array(x,np.float16).reshape(-1)
    y = np.array(y,np.float16).reshape(-1)
    map_xy = np.vstack((x,y))
    return np.sum(np.min(map_xy,axis=0))/np.sum(np.max(map_xy,axis=0))

def main():
    s=[[1,0.09,37,0.02],
       [4,0.36,12,0.06],
       [23,1.8,2.4,0.31],
       [110,0,0.55,1.20],
       [660,0,0.17,4.6]]
    t=[[0.559,0.051,42,0.015],
       [22.127,1.779,4.942,0.240],
       [24.736,2.621,1.530,1.182]]
    miny=[1,0,0.17,0.02]
    print(lsd(s,miny))
    print(lsd(t,miny))
    # 最小最大值评价度量
    thd1=[]
    for i in range(0,3):
        p=lsd(t,miny)[0+i*4:4+i*4]
        for j in range(0,5):
            q=lsd(s,miny)[0+j*4:4+j*4]
            thd1.append(minMaxDist(p,q))
    for m in range(0,3):
        print(thd1[0+5*m:5+5*m])

if __name__ == "__main__":
    main()

得到湖泊1与各营养等级之间的贴近度为：

0.9995

0.5176

0.7153

0.344

0.248

湖泊2与各营养等级之间的贴近度为：

0.7236

0.688

0.9854

0.45

0.32

湖泊3与各营养等级之间的贴近度为：

0.5254

0.3909

0.704

0.6543

0.472

因此根据最大隶属度原则，可以知道三个湖泊水体营养等级分别为：极贫营养、中营养、中营养

注意：上述代码只需要改变标准库标准或样品库指标数据以及各个指标的最小值即可。

例题2——土壤质量识别

#只需要更改标准指标矩阵的值和样品指标矩阵的值就ok了 
    s=[[10,23.35,0.1204,74.88,0.092],
       [17,36.09,0.2523,99.54,0.2592],
       [30,150,0.6,150,0.45],
       [50,350,1.4,350,1.05],
       [70,500,2,500,1.5]]
    x=[[14,67.3,0.12,59.9,0.29],
       [4.33,37.1,0.21,53.6,0.15],
       [5.95,46.5,0.23,56.1,0.12]]
    miny=[10,23.35,0.1204,74.88,0.092]

结果报告省略了，这个题在很多教材上应该都会摆出来，就不贴题目了

四、总结

        在模糊识别时一定要注意这个流程，在总结部分再次叙述一遍流程，也可以在目录中来看。

        ① 标准库隶属度转化

        ② 样本库隶属度转化

        ③ 样本库隶属度一一对应计算贴近度

        ④ 最大贴近度判断所述模式

        最后，感谢您看到这里啦~笔者是数模学习小白，希望对你有帮助，如果有错误敬请斧正！一起加油！