简单易懂 MySQL 高级部分 —— 索引篇

前言：本文内容基于 - 高性能MySQL（第三版）以及 极客时间：MySQL实战45讲

第一次写博客，格式或内容可能存在不当之处，请各位多多理解并支持，我会及时进行更改。

一、索引基础

1.1 什么是索引

大佬：好家伙，这一上来就给我整不会了，什么是索引，老师没有告诉过你，把索引看作图书的目录。 就这点小问题还需要我来讲 ？？？

我：停停停，别骂了别骂了，我当然知道可以看成是目录，我是问然后呢…这个目录倒是很容易看明白，我可以根据目录很快找到我想要的内容，但是这个索引呐…

show index from table_name; // 查询 table_name 中的索引

需要说明的是，查出来的索引有15个字段，但是由于目前并不涉及到具体的内容，故只截取了其中的一部分。


小白（理直气壮）：来来来，你看看，你让我怎么理解这个索引，你让我怎么去看作目录嘛。有没有更加通俗易懂的表述，让我明白索引到达做了什么事情。

大佬：一阵深思…似乎明白了你的困惑了，那么这样，你找出下面这句话的主干部分。

索引（在MySQL中也叫 “键（key）”）是存储引擎用于快速找到记录的一种数据结构。

                                                                                                    —— 高性能MySQL（第三版）— 第五章

我：* 索引是一种数据结构。(加 * 是重点，要考的哦！)

我：答对了，索引的本质其实就是一种数据结构，通过数据结构与一定的算法，那么索引就能够快速的在数据库中定位到需要的数据。

我：emmmm…好像明白了，又好像没明白，所以说索引的数据结构到底是什么，为什么能够快速找到内容。

大佬：安啦安啦，这个数据结构到底是什么，为什么能快速找到内容，这个就在下一节课再讲呢，现在你只需知道一件事情 索引是一种数据结构，索引的作用与目录类似，可以快速定位内容。

1.2 索引的本质与类型

1.2.1 索引的进化之路（索引的本质）

我（期待的）：大佬，现在可以说说索引的本质是什么了吗，到底是什么数据结构呢。

大佬：MySQL现在的默认引擎是 InnoDB，而 InnoDB 引擎主要采用了 B+树 的数据结构，虽然后面也会涉及到其他的数据结构，不过现阶段你可以简单的理解为 MySQL 索引的本质是 B+树。

我：啊？B+树是什么啊？为什么要用B+树？它有什么优势吗？

大佬（无语）：简直服了你了，那么我们暂时先不讲B+树，先来说说数据结构吧。

我：为什么又要说数据结构呢？

大佬：那你知道什么是 B+树 吗？

我（弱弱的）：不知道…

1.2.1.1 基于数组和单链表的索引

大佬：算了，懒得和你计较。那么现在我问你，如果让你来设计数据库的索引，你会用数组还是单链表？

我：都不用。

大佬：哦哟，聪明欸，那为什么呢？

我：虽然数组可以通过下标随机访问数据，但是对于数组来说，它并不知道数组内到底存放了什么数据，如果要按照内容进行查找时，最坏的情况需要查询所有的数据。同时，如果用数组进行组织，在对不是数组尾的数据进行操作时，需要对当前操作之后的所有数据进行前移或后移，极大影响了性能。

大佬：很不错，那链表呢。

我：链表虽然降低了增加和删除时的开销，但是查询时必须按顺序查找，查找的开销很大。

我：还有，不管是数组还是链表，如果对于大量的数据，根本无法加载到内存中。所以两种方式都可以用，但是只能用一点点。

1.2.1.2 基于二叉查找树（BST树）的索引

大佬：很好很好，说的很不错，那你能想到用什么方式呢？

我：肯定是用树呀，二叉查找树就很不错。

大佬：但索引并没有采用二叉查找树，你知道为什么吗？

我：emmmm…

大佬：好吧，假设现在数据库中有这么一组数据（见 图1.2.1.1）。

大佬：使用该组数据，我们来做一个查询（假设表名为 T）：

select * from T where number = 010;

如果我们并未给表建立任何索引 （事实上，即使我们不显式的创建索引，MySQL也会隐式的为我们创建主键索引，当然这是后话，和现在无太大的关系），那么执行此语句时，MySQL会进行全表扫描，即：从第一行开始，依次一行一行读取，直到最后一行结束。

1. 在没有索引的情况下：MySQL在第六次读取时，找到了我们想要的数据。
2. 此时我们建立 number 字段的二叉查找树索引，即右图，我们可以发现，仅需要一次就可以找到我们需要的数据，并且在三次内可以找到任何我们要查询的结果。

我：的确快了很多欸。

大佬（阴笑）：实际上根本不是这样的，这组数据只是我随手瞎掰出来的，现实中很难出现这样的数据。

如果你有认真学过数据结构就知道，二叉查找树有以下特点：

1. 左子树上所有结点的值均小于或等于它的根结点的值。
2. 右子树上所有结点的值均大于或等于它的根结点的值。
3. 左、右子树也分别为二叉排序树。

我：这个和特点有关系吗？？？

大佬：关系大了去了，那你现在尝试用二叉查找树对 id 字段建索引。

我：看我的…一顿操作…emmmmm…这个…我好像懂了…

这里给大家推荐一个可以模拟各种数据结构的网站，大家可以尝试自行推导这个过程，自己动手后才会更有收获，效果如下图。

大佬：这就是不用二叉查询树的重要原因之一，当我们需要按顺序存储数据时，此时建立的索引，其本质和单链表没有任何区别。当然还有另一个重要的原因，这个先卖个关子，留着后面解答。

1.2.1.3 基于二叉平衡树（AVL树）的索引

大佬：还有什么想法吗？

我：既然二叉查找树会产生单链表的情况，那我给它平衡一下，用二叉平衡树总行了吧。

大佬：挺自信啊，那你继续！

我：一顿操作…

好，果然是，通过实验验证，即使是按顺序的字段，通过二叉平衡树，现在也可以在三次之内找到任何一条数据，继续测试。

即使再多的数据也能够保持平衡，随机删除数据后仍然保持平衡，这一次肯定没有问题了。

大佬（淡定脸）：那你知道为什么 MySQL 还是没有采用二叉平衡树吗？

我（开始怀疑）：不知道。

大佬：这里强烈建议大家自己去用AVL树创建一些数据，越多越好，然后再随机删除一些数据。

我：我建了30多个数据，也删除了一些数据，都可以保持平衡啊，没问题啊。

大佬：那你不觉得这个过程很慢吗？

我：欸？没发现欸。

大佬：二叉平衡树虽然弥补了二叉树极端情况下单边过长的问题，但是同时也引入了新的问题，即：为了保持绝对的平衡，二叉平衡树在插入或删除时，要计算不同节点的平衡因子，并且可能会造成一次或多次的AVL旋转，对于大型或经常添加删除的数据库，计算量会更大，旋转的次数可能也会更多，这就造成了极大的额外开销。 同样，红黑树虽然只进行局部的平衡，减少了选择次数与计算量，但是面对大量数据时，仍然会造成大量的开销。

当然，这里要解释前面埋下的坑，不用二叉树的第二个重要原因：在面对大量的数据时，树的高度过高。

我们知道，深度为k的二叉树，最多有 2^k-1 个节点。
通过计算，可得知，对于千万级别（1600万左右）的数据，树的深度达到了 25 层。
不要以为 25 层不多，需要知道的是，一层代表着一次 IO 操作，而 IO 操作的效率如何大家都清楚，其次，我们现在所说的都只是一个字段的情况，若非主键索引，可能还会出现回表（回表后面会详细讲）的情况，可理解为一条数据会造成多次查询。

不使用二叉树或者是二叉平衡树的第三个原因还在于：二叉树和二叉平衡树不支持范围查找。 范围查找是数据库最常用的查找之一，对于不支持范围查找的二叉树和二叉平衡树来说，需要多次从根节点进行遍历。在结合前面所说的，在千万级别的数据库中，对于查找范围在 10 之内的数据，极端情况下可能会遍历 250 次（不包括回表次数）。按照一次 IO 操作 10ms 来计算，查找时间高达 10 * 0.25 = 2.5s。对于任何一个查询来说，这都是一个无法忍受的时间。

并且，上面说的都还是理想情况下，在实际开发过程中，可能出现的问题会更加难以预测，所有现在还用二叉树和二叉平衡树了吗？？？

我：不用了，不用了…就一个简简单单的查询，搞那么多花样干哈呀！！！

大佬：孩子，我劝你一句，MySQL里面的水很深，你把握不住，还是好好的当一个 CRUD 程序员吧。

1.2.1.4 基于多叉平衡树（B树）的索引

我：大佬，大佬，我又想到了， 多叉平衡树 就完美解决了上面的问题，那为什么不用 B树 呢，非要用什么 B+树。

大佬：如果你知道 B+树 的结构，那你就知道为什么选择 B+树，而非 B树。当然，在说B+树 之前，我还是先考考你有关于 B树 的知识点。

我：来吧！！！

大佬：你先说说你理解的 B树。

我：好，先上图！

这是一个4阶B树，在我看来，其实就是一个加强版的AVL树。
相比于 AVL 树来说：

• B树至少有两个子节点，至多有 m 个子节点，称之为 m阶 B树。
• B树的每个节点至少能存储一个数据（或叫关键字），之多存储 m-1 个数据（关键字）。

按照B树的计算公式可以得出，对于一个深度为4的4阶B树，最多可以存储：
                                        (4-1) * (4⁰+4¹+4²+4³) = 255

由此可见，如果再增大m，那么B树能够存储的数据就更多，并且B树也是平衡树，可以避免按顺序存储时出现单边过长的问题。

大佬：可以可以，大体上都说在点子上了，理论基本上都过关了。

大佬：那我再问几个问题

1. 前面讲过，二叉平衡树为了保持平衡，需要一定系统开销，那么B树也是平衡树，你觉得B树的系统开销如何呢？
2. 同样也是前面提到过的，二叉树不支持范围查找，那B树，你觉得B树是否支持范围查找？
3. 假设现在有一千多万个整数类型的数据，你会用B树怎么涉及索引呢？

我：…

大佬：接下来，需要你忘记之前的那些图片，前面所提到的各种，都是关于树的一些数据结构图，但是作为索引，其构造是不一样的。下面以B树为例子。

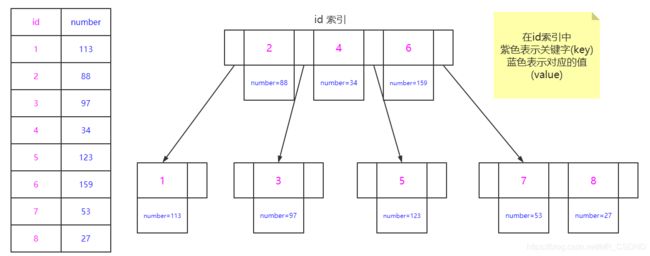
索引的构造想必大家都清楚，就是键值对，键（key）很好理解，就是我们创建的索引字段的值（单一索引，只有一个字段的索引），那键对应的值是什么呢，为什么这里的值是 id 呢，有些小伙伴可能问为什么不是该条数据的地址呢？。

补充一下，我们目前主要以MySQL的InnoDB引擎进行的讲解，而 InnoDB引擎采用的是聚簇索引。

再简单理解一下聚簇和非聚簇引擎：

• 聚簇索引中的值（value）是具体的数据。
• 非聚簇索引中的值（value）不是数据本身，而是数据存放的地址。

解决完第一个问题，现在来做一个查询（假设表面为T）。

select * from T where number = 159;

如果我们走 number 索引去查找，那么通过图我们可知，查出来的是 number = 159 时所对应的 id 值，那么要得到我们的数据，还得再次去查找 id = 6 的数据。这就是前面所提到的 回表 的操作，即对一条记录的查询可能会多次查表。

现在，再给出 id 的索引，需要注意的是，id 索引是主键索引。 至于什么是主键索引，这个问题一会再解释。

所以该查询的结果为：

id = 6 | number = 159 .

我（开始迷糊）：这这这…你通过 number 索引查出来 id 值，再通过 id 索引查出来 number，这不是脱了裤子放屁——多此一举嘛！

大佬（无语）：…

大佬：好吧，那我把这个表修改一下，你可能就明白了。

现在，我给表新增了一个字段（op），此时，你会发现 id 索引的值中也增加了对应的 op 字段的值。

这就是主键索引的作用：主键索引会存放该条记录的所有值。
注意前面的问题，我们要查询的数据是 * ，即所有的数据，所以才会有回表的操作，如果我们换一个问题：

select id from T where number = 159;

此时，查询结果就不需要回表进行处理，因为 number 索引查出来的值就是 id，这有另一个专业术语 索引覆盖，这里至少简单提一下，后续会详细讲解。

当然，这里也解释开篇所说的一个问题，即使我们不主动创建索引，MySQL也会隐式的为我们创建一个主键索引，因为在没有索引覆盖的情况下，查询都会进行回表操作。

大佬：好像扯远了，不够就相当于给大家做一个知识的补充和提前预习吧，现在知道了索引的结果，回到前面的问题，我们先来解决第三个问题。

要解决这个问题，那么还需要扩展一个知识点，MySQL的最小存储单位为页，一个叶子节点就是一页，MySQL中页的默认大小为 16k。为了更清楚的认识，用一张图来表示。

在计算之前，我们还需要在提示一点的是，通过MySQL的源码可以知道，MySQL给每个指针分配的大小是 6字节 。

一个指针加一个键值对的大小为 ：6+4+4=14 Byte
一页的大小： 16k = 16 * 1024 = 16384 Byte
指针的数量 = 键值对的数量 + 1
故，减去一个指针，一页剩余的大小为：16384 - 6 = 16387 Byte

一页最多能容纳的键值对数量为： 16387 / 14 = 1169.8571 = 1169 【向下取整】

而此时，一页有 1169 + 1 = 1170 个指针

(1170-1) * (1170⁰ + 1170¹ + … + 1170^h-1) = 存储的数据量

大致计算可以得出：h = 2 时，数据量为 134万; m = 3 时，数据量为 16亿。

由此，可以看出，B树相对于二叉树来讲，数据存储量的提升是几个数量级的提升，当然，这里演示的只是存储较小的字段信息，当数据字段增大时，存储量会相应的减小，但是一般来说，在MySQL中，深度为3的B树，至少可以存储千万级别的数据量。

大佬：解决了第三个问题，再来说第一个问题，其实现在已经很容易得出结论了。因为树的深度变浅了，且每个节点存储量大大增加，相比于二叉平衡树和红黑树来说，B树的自旋次数被极大的减少，但是B树的每次旋转都伴随着更加的系统开销。

大佬：最后一个问题，也是显而易见的，B树可以认为二叉平衡树的升级，只是运行每个节点可以有多个子节点，但其他的并无改变，故B树仍然不支持范围查找。

我：我突然觉得程序员这一行可能不太适合我…

大佬：不要觉得很难，每个人都是这样过来的，我一开始什么都不知道，就硬啃书和视频，看完了也是不知所云，感觉什么都没有学到。后来发现我是为了学而学，完全没有融入这个学习的过程。再后来，我开始自己动手去跟着做，慢慢找到了感觉，开始喜欢上了这些东西，我感觉我打开了新世界的大门，原来这里面还有这么多有趣的东西…

兴趣永远是最好的老师，如果你觉得学不进去了，可以停下来思考思考，自己是否要走这条路，如果选择坚持走下去，那么就尝试让自己找到其中的乐趣，然后再出发。

我：我知道了！！！我一定会融入其中的。

1.2.1.5 基于B+树的索引

大佬：那我们就成热打铁，把最后这一点说了吧。

我：好！！！

大佬：我们先来粗略的见识一下B+树的结构。

我：发现了！B+树 比 B树 多了一个指针。

大佬：这是结构上的一个重要的改变，那么我们再来看看更加详细的结构。

现在，我们来说说这其中的变化
第一个改变：叶子节点用指针连接了起来。
第二个改变：B+树中出现了重复的数据。 用指针表示出来的四处。
第三个改变：除了叶子节点有值（value）外，其余节点都只有键（key）。

先解决第三个：思考一下，删除除叶子节点外的节点的值有什么好处。当然是为什么存放更多的索引。想想在 B树 处的计算，每一页只有 16k ，在 B树 中，我们每一页都存放的有键值对，计算出来深度为 3 的 B树可以存放 16亿 的数据。

现在来看看 B+树 能存放多少数据。

因为除叶子节点外的节点没有存储值信息，所以一对 指针+键 的大小为： 4+6 = 10 Byte
一页大小： 16K = 1024 * 16 = 16384 Byte
指针的数量 = 键值对的数量 + 1
故，减去一个指针，一页剩余的大小为：16384 - 6 = 16387 Byte

一页最多能容纳的数据的数量为： 16387 / 10 = 1638.7 = 1638 【向下取整】

而此时，一页有 1638 + 1 = 1639 个指针

对于含有叶子节点的页来说，与B树存储容量相同，为：1169 个

(1639-1) * (1639⁰ + 1639¹ + … + 1639^h-2) * 1169 = 存储的数据量

大致计算可以得出：h = 2 时，数据量为 191万; h = 3 时，数据量为 31亿。

从计算中可以看出，B+树的存储量远大于B树（因为这里 value值 只有 4Byte，所以最终结果并不明显）

好了，现在来看第一个改变：B+树在叶子节点使用了链表。

这个链表有什么用处呢？

现在我们可以看出一件事情：所有的叶子节点的键（key），是按照从左至右依次递增的顺序。 这是一个很重要的点，现在我们来做一个查询：

select * from T where number between 15 and 40;

现在我们来看MySQL会怎么进行范围查找：

1. MySQL根据索引查找到第一个符合条件的记录
2. MySQL继续向右查找下一个数据，直到找到第一个不符合条件的记录为止。

现在，我们可以看出B+树中指针的作用了，将所有的数据连在一起，以便支持快速的范围查找，而不需要从头再进行遍历。

同样，也说明了，为什么B+树中会存在重复的键（key）信息：除了叶子节点外的节点，键仅是充当了一个快速定位到数据的作用，而叶子节点中的键（key）是为了将所有的键（key）进行连起来，为范围查找提供服务。

我：原来如此，这也是为什么MySQL采用B+树的原因，在极大减少IO操作（降低了树的深度）的情况下，又极大的提供了存储量，同时还支持范围查找。 那些开发者都是怎么想到这么东西的啊，太不可思议了。

大佬：无他，在不断的试错与经验中前行，就像我们从数组开始一步一步慢慢过渡到B+树，不断的发现问题并解决问题，所有的技术都是不断的迭代，才到现在这一步的。你以为B+树已经很完善了吗，当然不是，B+树也存储很多问题，只不过相比于前面的技术的来说，在索引这方面，显得微不足道的罢了。

B+树最大的性能问题在于会产生大量的随机IO，主要存在以下两种情况：

• 主键不是有序递增的，导致每次插入数据产生大量的数据迁移和空间碎片；
• 即使主键是有序递增的，大量写请求的分布仍是随机的；

大佬：那么到现在为止，MySQL索引的本质部分已经学的差不多了，现在做一个简单的总结来结束本篇内容吧。

1.2.1.6 总结

基于各种数据结构的索引的优缺点：

• 数组的或单链表 —— 基本上为全表扫描，且存在无法全部装进内存的问题。
• 二叉树 —— 存在失衡的情况，大量数据时树的深度过大 ，不支持范围查找。
• AVL树 —— 解决了失衡的情况，但是有极大的自旋开销，树的深度过大，不支持范围查找。
• B树 —— 解决了树的深度问题，不支持范围查找。
• B+树 —— 进一步解决了树的深度问题，支持范围查找。

二、索引的优点

三、高性能索引策略

四、索引案例学习

五、维护索引表

六、总结