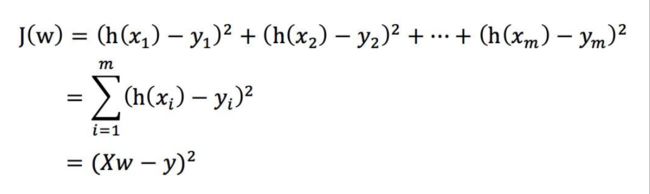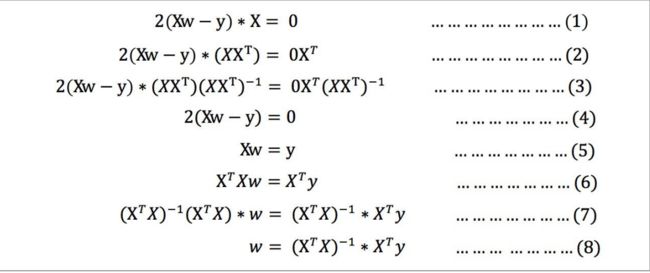机器学习算法 02 —— 线性回归算法(正规方程、梯度下降、模型保存)
文章目录
- 系列文章
- 线性回归
- 1 线性回归简介
- 2 线性回归API初步使用
- 3 数学求导复习
- 4 线性回归的损失和优化
-
- 4.1 损失函数
- 4.2 优化算法
-
- 正规方程
- 梯度下降
-
- 梯度下降生动解释
- 梯度的概念
- 梯度下降公式
- 小结
- 5 梯度下降方法介绍(了解即可)
-
- 5.1 详解梯度下降算法
-
- 相关概念复习
- 梯度下降法的推导
- 5.2 梯度下降法家族
-
-
- 全梯度下降算法(FG)
- 随机梯度下降算法(SG)
- ⼩批量梯度下降算法(Mini-Batch)
- 随机平均梯度下降算法(SAG)
-
- 6 线性回归API详解
- 7 案例:波士顿房价预测
-
- 7.1 数据集介绍
- 7.2 回归模型评估
- 7.3 代码实现
- 8 欠拟合和过拟合
-
- 8.1 定义
- 8.2 原因和解决方法
- 8.3 正则化
- 9 正则化线性模型
-
- 9.1 岭回归
- 9.2 Lasso回归
- 9.3 弹性网络(Elastic Net)
- 9.4 小结-如何选择正则化方法?
- 11 波士顿房价预测—岭回归
- 12 模型的保存和加载
系列文章
机器学习算法 01 —— K-近邻算法(数据集划分、归一化、标准化)
机器学习算法 02 —— 线性回归算法(正规方程、梯度下降、模型保存)
机器学习算法 03 —— 逻辑回归算法(精确率和召回率、ROC曲线和AUC指标、过采样和欠采样)
机器学习算法 04 —— 决策树(ID3、C4.5、CART,剪枝,特征提取,回归决策树)
机器学习算法 05 —— 集成学习(Bagging、随机森林、Boosting、AdaBost、GBDT)
机器学习算法 06 —— 聚类算法(k-means、算法优化、特征降维、主成分分析PCA)
机器学习算法 07 —— 朴素贝叶斯算法(拉普拉斯平滑系数、商品评论情感分析案例)
机器学习算法 08 —— 支持向量机SVM算法(核函数、手写数字识别案例)
机器学习算法 09 —— EM算法(马尔科夫算法HMM前置学习,EM用硬币案例进行说明)
机器学习算法 10 —— HMM模型(马尔科夫链、前向后向算法、维特比算法解码、hmmlearn)
线性回归
学习目标:
- 掌握线性回归的实现过程
- 应⽤LinearRegression或SGDRegressor实现回归预测
- 知道回归算法的评估标准及其公式
- 知道过拟合与⽋拟合的原因以及解决⽅法
- 知道岭回归的原理及与线性回归的不同之处
- 应⽤Ridge实现回归预测
- 应⽤joblib实现模型的保存与加载
1 线性回归简介
线性回归应用场景:房价预测、销售额度预测、贷款预测……
线性回归(Linear regression)定义:是利⽤回归⽅程(函数)对⼀个或多个⾃变量(特征值)和因变量(⽬标值)之间关系进⾏建模的⼀种分析⽅式。
- 只有一个自变量叫单变量回归,多个自变量叫多元回归
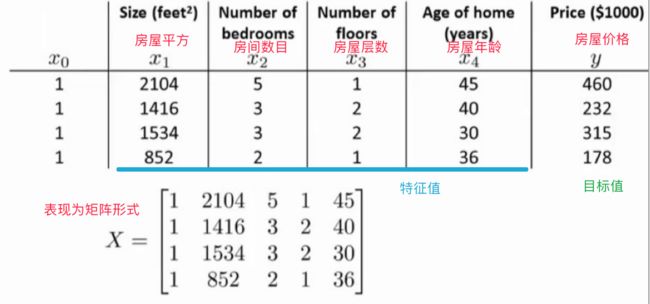
- 线性回归用矩阵(线性代数里面的)来举例:
-
线性模型:
例如 期末成绩=0.7x考试成绩+0.3x平时成绩, 房⼦价格 = 0.02×中⼼区域的距离 + 0.04×城市⼀氧化氮浓度 + (-0.12×⾃住房平均房价) + 0.254×城镇犯罪率 这种特征值(考试成绩和平时成绩)与目标值(期末成绩)建立了一个关系,就是线性模型。
在线性回归中,主要有两种模型,一种是线性关系,另一种是非线性关系。
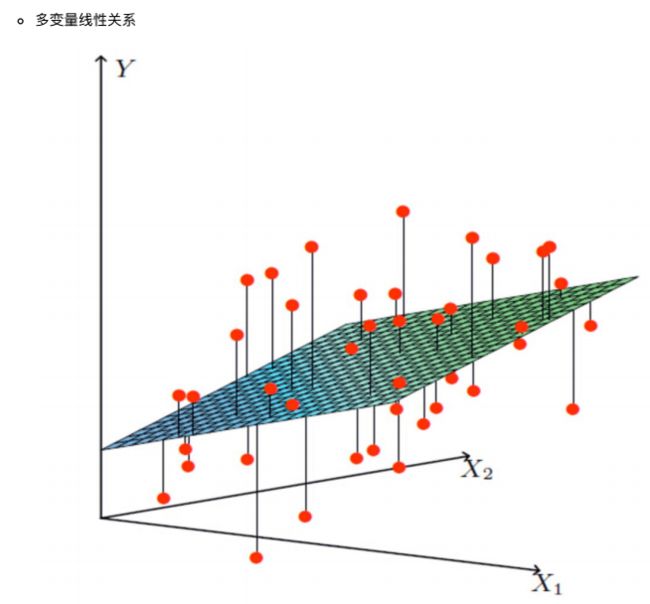
- 线性关系:包括单变量线性关系(直线)和多变量线性关系(平面)
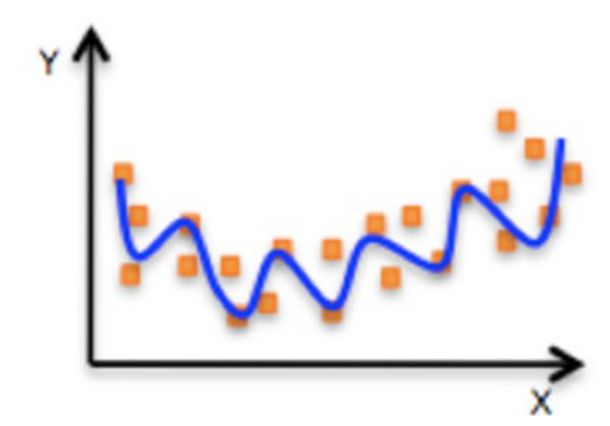
- 非线性关系:下图回归方程可以理解为 y = w 1 x 1 + w 2 x 2 2 + w 3 x 3 3 y=w_{1}x_{1}+w_{2}x_{2}^2+w_{3}x_{3}^3 y=w1x1+w2x22+w3x33
2 线性回归API初步使用
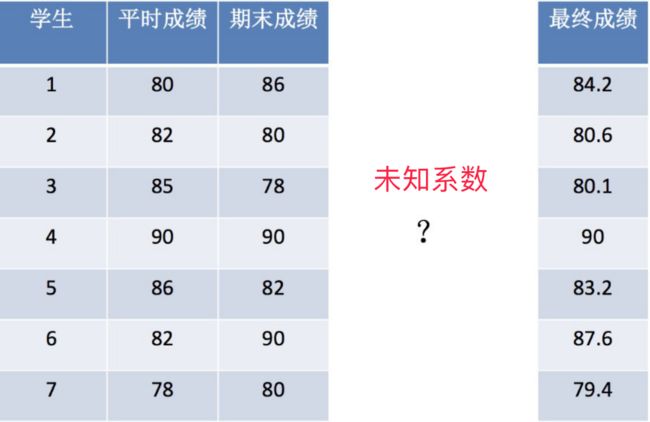
后面会详细讲,这里只是简单举例。就用前面计算期末成绩那个例子,假设现在有如下成绩,我们通过线性回归求出未知系数,得出平时成绩、期末成绩与最终成绩的关系,然后输入新成绩进行预测。
由于只是初步简单使用,所以机器学习流程的一些步骤会省略:
- 1.获取数据集
- 2.数据基本处理(该案例中省略)
- 3.特征⼯程(该案例中省略)
- 4.机器学习
- 5.模型评估(该案例中省略)
sklearn.linear_model.LinearRegression(),这里用到返回对象的一个属性LinearRegression.coef_,可查看回归系数。
from sklearn.linear_model import LinearRegression
# 1. 获取数据
x = [[80, 86],
[82, 80],
[85, 78],
[90, 90],
[86, 82],
[82, 90],
[78, 80],
[92, 94]] # 平时成绩 期末成绩
y = [84.2, 80.6, 80.1, 90, 83.2, 87.6, 79.4, 93.4] # 最终成绩
# 4. 机器学习 - 线性回归
# 4.1 实例化估计器
estimator = LinearRegression()
# 4.2 模型训练
estimator.fit(x, y)
print("回归系数:", estimator.coef_)
print("预测 平时成绩 100 期末成绩 80的最终成绩:", estimator.predict([[100, 80]]))
3 数学求导复习
常见函数的倒数
导数的四则运算
4 线性回归的损失和优化
前面房子价格例子中,存在这样关系:
真实关系:真实房⼦价格 = 0.02×中⼼区域的距离 + 0.04×城市⼀氧化氮浓度 + (-0.12×⾃住房平均房价) + 0.254×城镇犯罪率
而我们一开始并不知道真实关系,所以我们随意指定参数:
随机指定关系:预测房⼦价格 = 0.25×中⼼区域的距离 + 0.14×城市⼀氧化氮浓度 + 0.42×⾃住房平均房价 + 0.34×城镇犯罪率
这样得出的房子价格肯定就存在一定误差,就像下图,这个误差也称为损失,最终目标就是让这个损失减少。
我们可以根据下图紫色点到红线和绿线的距离来判断,距离越大的线,说明损失越大。如此就能判断谁才是真实关系。
4.1 损失函数
损失函数定义:
- y i y_{i} yi是第i个训练样本的真实值
- h ( x ) i h(x)_{i} h(x)i是第i个训练样本特征值组合成的预测函数(函数计算完的结果就是预测值)
- w w w是损失值, w w w最小说明损失越小,说明线性模型越好。
- 这个式子也称为最小二乘法
如何减少损失值,使得预测更加准确呢?我们一直说机器学习有自动学习的功能,而这在线性回归里就能得到很好的体现,我们可以通过优化算法来优化回归的损失!
4.2 优化算法
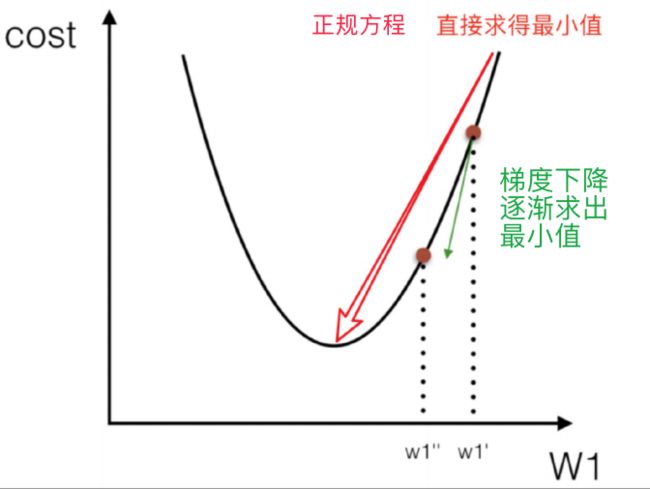
正规方程
正规方程公式: w = ( X T X ) − 1 X T y w=(X^TX)^{-1}X^Ty w=(XTX)−1XTy,其中 X X X是特征值矩阵, y y y是目标值矩阵。
优点:正规方程可以直接求出最好结果(即最小损失)
缺点:由于涉及到矩阵运算,当特征过多时矩阵运算变得很复杂,求解速度会很慢。所以只适用于小数据量。
以上面房价预测举例:
运用正规方程求解:
扩展:正规方程的推导过程
把上面损失函数公式换成矩阵的写法:
其中, X X X是特征值矩阵, w w w是权重矩阵, y y y是目标矩阵,对其求解关于 w w w的最⼩值。
式(1)到式(2)推导过程中, X是⼀个m⾏n列的矩阵,并不能保证其有逆矩阵,但是右乘XT把其变成⼀个⽅阵,保证其有逆矩阵。
式(5)到式(6)推导过程中,和上类似。
梯度下降
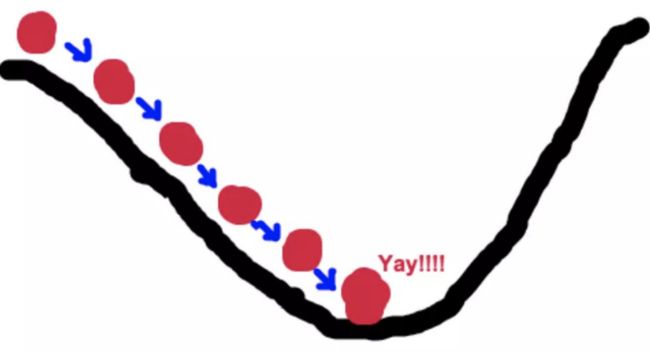
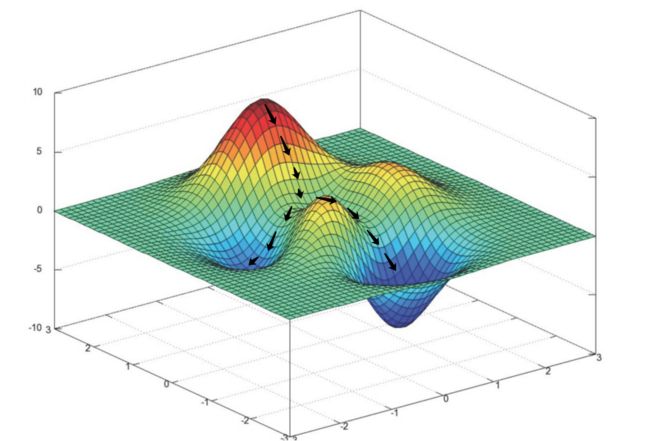
梯度下降法的基本思想可以看做是⼀个下⼭的过程。
梯度下降生动解释
⼀个⼈被困在⼭上,需要从⼭上下来(i.e. 找到⼭的最低点,也就是⼭⾕)。但此时⼭上的浓雾很⼤,导致可视度很低。因此,下⼭的路径就⽆法确定,他必须利⽤⾃⼰周围的信息去找到下⼭的路径。
具体的操作就是以他当前的所处的位置为基准,寻找这个位置最陡峭的地⽅,然后朝着⼭的⾼度下降的地⽅⾛,(同理,如果我们的⽬标是上⼭,也就是爬到⼭顶,那么此时应该是朝着最陡峭的⽅向往上⾛)。然后每⾛⼀段距离,都反复采⽤同⼀个⽅法,最后就能成功的抵达⼭⾕。
梯度下降的基本过程就和下⼭的场景类似。
-
⾸先,我们有⼀个可微分的函数。这个函数就代表着⼀座⼭。 我们的⽬标就是找到这个函数的最⼩值,也就是⼭底。
-
根据场景假设,最快的下⼭的⽅式就是找到当前位置最陡峭的⽅向,然后沿着此⽅向向下⾛。
-
对应到函数中,就是找到给定点的梯度,然后朝着梯度相反的⽅向,就能让函数值下降的最快(梯度的⽅向是函数值上升最快的⽅向)。重复利⽤这个⽅法,反复求取梯度,最后就能到达局部的最⼩值。
-
求取梯度就确定了最陡峭的⽅向,也就是场景中测量⽅向的⼿段。
梯度的概念
梯度是微积分(高等数学)中⼀个很重要的概念
- 在单变量的函数中,梯度其实就是函数的微分,代表着函数在某个给定点的切线的斜率;
- 在多变量函数中,梯度是⼀个向量,向量有⽅向,梯度的⽅向就指出了函数在给定点的上升最快的⽅向;
这也就说明了为什么我们需要千⽅百计的求取梯度!我们需要到达⼭底,就需要在每⼀步观测到此时最陡峭的地⽅,梯度就恰巧告诉了我们这个⽅向。梯度的⽅向是函数在给定点上升最快的⽅向,那么梯度的反⽅向就是函数在给定点下降最快的⽅向,这正是我们所需要的。所以我们只要沿着梯度的反⽅向⼀直⾛,就能⾛到局部的最低点!
梯度下降公式
公式: θ i + 1 = θ i − α σ σ θ i J ( θ ) \theta_{i+1}=\theta_{i}-\alpha\cfrac{\sigma}{\sigma\theta_{i}}J(\theta) θi+1=θi−ασθiσJ(θ)
-
σ σ θ i J ( θ ) \cfrac{\sigma}{\sigma\theta_{i}}J(\theta) σθiσJ(θ)就是梯度,也就是 J ( θ ) J(\theta) J(θ)求导
-
α \alpha α
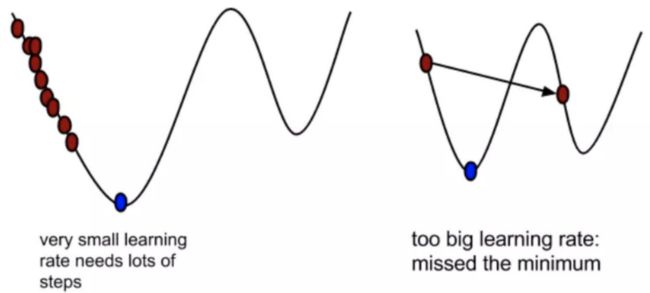
α \alpha α是学习率(或叫步⻓),我们可以通过α来控制每⼀步⾛的距离,以保证每一步不要⾛太大,错过了最低点。同时也要保证不要⾛的太慢,导致太阳下⼭了,还没有⾛到⼭下。所以α的选择在梯度下降法中往往是很重要的!α不能太⼤也不能太⼩,太⼩的话,可能导致迟迟⾛不到最低点,太⼤的话,会导致错过最低点!
-
为什么梯度要乘以⼀个负号?
梯度前加⼀个负号,就意味着朝着梯度相反的⽅向前进!我们在前⽂提到,梯度的⽅向实际就是函数在此点上升最快的⽅向!⽽我们需要朝着下降最快的⽅向⾛,⾃然就是负的梯度的⽅向,所以此处需要加上负号
正因为有梯度下降这样的优化算法,所以线性回归有了自动学习的能力!
注意:梯度下降不一定能得到最小值,只能保证得到极小值,例如下图中的箭头,因为在试探时左右两边都可能出现山谷,当进入左边山谷时会发现周围都比较高,于是认为左边山谷就是最低点。这种只能算极小值,最小值在右边山谷的。
小结
-
损失函数【知道】
- 最⼩⼆乘法
-
线性回归优化⽅法【知道】
- 正规⽅程
- 梯度下降法
-
正规⽅程 – ⼀蹴⽽就【知道】
- 利⽤矩阵的逆,转置进⾏⼀步求解
- 只是适合样本和特征⽐较少的情况
-
梯度下降法 — 循序渐进【知道】
- 梯度的概念
- 梯度下降公式
-
梯度下降法中关注的两个参数
- α – 就是步⻓
- 步⻓太⼩ – 下⼭太慢
- 步⻓太⼤ – 容易跳过极⼩值点(*****)
- 为什么梯度要加⼀个负号
- 梯度⽅向是上升最快⽅向,负号就是下降最快⽅向
- α – 就是步⻓
-
梯度下降法和正规⽅程选择依据【知道】
- ⼩规模数据:
- 正规⽅程:LinearRegression(但不能解决拟合问题)
- 岭回归
- ⼤规模数据:
- 梯度下降法:SGDRegressor
- ⼩规模数据:
5 梯度下降方法介绍(了解即可)
上⼀节中介绍了最基本的梯度下降法实现流程,本节我们将进⼀步介绍梯度下降法的详细过算法推导过程和常⻅的梯度下降算法。
PS:涉及到大量公式以及数学推导,建议先跳过,后面有需要再看。
5.1 详解梯度下降算法
相关概念复习
在详细了解梯度下降的算法之前,我们先复习相关的⼀些概念。
-
步长:
步⻓决定了在梯度下降迭代的过程中,每⼀步沿梯度负⽅向前进的⻓度。⽤前⾯下⼭的例⼦,步⻓就是在当前这⼀步所在位置沿着最陡峭最易下⼭的位置⾛的那⼀步的⻓度。
-
特征:
指的是样本中输⼊部分,⽐如2个单特征的样本 ( x ( 0 ) , y ( 0 ) ) , ( x ( 1 ) , y ( 1 ) ) (x^{(0)},y^{(0)}),(x^{(1)},y^{(1)}) (x(0),y(0)),(x(1),y(1)),则第⼀个样本特征为 x ( 0 ) x^{(0)} x(0),第⼀个样本输出为 y ( 0 ) y^{(0)} y(0)。
-
假设函数:
在监督学习中,为了拟合输⼊样本,⽽使⽤的假设函数,记为 h θ ( x ) h_{\theta}(x) hθ(x)。⽐如对于单个特征的m个样本 ( x ( i ) , y ( i ) ) ( i = 1 , 2 , . . . m ) (x^{(i)},y^{(i)})(i=1,2,...m) (x(i),y(i))(i=1,2,...m),可以采用的拟合函数为: h θ ( x ) = θ 0 + θ 1 x h_{\theta}(x)=\theta_{0}+\theta_{1}x hθ(x)=θ0+θ1x
-
损失函数:
为了评估模型拟合的好坏,通常⽤损失函数来度量拟合的程度。损失函数极⼩化,意味着拟合程度最好,对应的模型参数即为最优参数。
在线性回归中,损失函数通常为样本输出和假设函数的差取平⽅。⽐如对于m个样本 ( x i , y i ) ( i = 1 , 2 , . . . m ) (x_{i},y_{i})(i=1,2,...m) (xi,yi)(i=1,2,...m),采⽤线性回归,损失函数为: J ( θ 0 , θ 1 ) = ∑ i = 1 m ( h θ ( x i ) − y i ) 2 J(\theta_{0},\theta_{1})=\sum\limits_{i=1}^m(h_\theta(x_i)-y_i)^2 J(θ0,θ1)=i=1∑m(hθ(xi)−yi)2,其中 x i x_i xi表示第i个样本, y i y_i yi表示第i个样本的输出, h θ ( x i ) h_{\theta}(x_i) hθ(xi)为假设函数。
梯度下降法的推导
1、先决条件
先确定优化模型的假设函数和损失函数。
比如对于线性回归,假设函数设为 h θ ( x 1 , x 2 , . . . x n ) = θ 0 + θ 1 x 1 + . . . + θ n x n h_\theta(x_1,x_2,...x_n)=\theta_0+\theta_1x_1+...+\theta_nx_n hθ(x1,x2,...xn)=θ0+θ1x1+...+θnxn,其中 θ i ( i = 0 , 1 , 2... n ) \theta_i(i=0,1,2...n) θi(i=0,1,2...n)是模型参数, x i ( i = 0 , 1 , . . . n ) x_i(i=0,1,...n) xi(i=0,1,...n)是每个样本的n个特征值。这个表示可以再简化下,我们增加一个特征 x 0 = 1 x_0=1 x0=1,将其表示为 h θ ( x 0 , x 1 , . . . x n ) = ∑ i = 0 n θ i x i h_\theta(x_0,x_1,...x_n)=\sum\limits_{i=0}^n\theta_ix_i hθ(x0,x1,...xn)=i=0∑nθixi
同样是线性回归,对于上面的假设函数,其损失函数为: J ( θ 0 , θ 1 . . . , θ n ) = 1 2 m ∑ j = 0 m ( h θ ( x 0 ( j ) , x 1 ( j ) , . . . x n ( j ) ) − y j ) 2 J(\theta_0,\theta_1...,\theta_n)=\frac{1}{2m}\sum\limits_{j=0}^m(h_\theta(x_0^{(j)},x_1^{(j)},...x_n^{(j)})-y_j)^2 J(θ0,θ1...,θn)=2m1j=0∑m(hθ(x0(j),x1(j),...xn(j))−yj)2
2、算法相关参数初始化
主要是初始化 θ 0 , θ 1 . . . , θ n \theta_0,\theta_1...,\theta_n θ0,θ1...,θn,算法终止距离 ϵ \epsilon ϵ和步长 α \alpha α。在没有任何先验知识的时候,通常将所有的 θ \theta θ初始化为0,将步长 α \alpha α初始化为1。
3、推导过程
-
确定当前位置的损失函数的梯度,对于 θ i \theta_i θi其梯度表达式如: σ σ θ i J ( θ 0 , θ 1 . . . , θ n ) \cfrac{\sigma}{\sigma\theta_i}J(\theta_0,\theta_1...,\theta_n) σθiσJ(θ0,θ1...,θn)
-
用步长乘以损失函数的梯度,得到当前位置下降的距离,即 α σ σ θ i J ( θ 0 , θ 1 . . . , θ n ) \alpha\frac{\sigma}{\sigma\theta_i}J(\theta_0,\theta_1...,\theta_n) ασθiσJ(θ0,θ1...,θn),这对应于登山例子中的一步。
-
确定是否所有的 θ \theta θ,梯度下降的距离都⼩于 ϵ \epsilon ϵ,如果⼩于 ϵ \epsilon ϵ则算法终⽌,当前所有的 θ i ( i = 0 , 1 , . . . n ) \theta_i(i=0,1,...n) θi(i=0,1,...n)即为最终结果。否则进⼊下一步。
4、持续推导
更新所有的 θ \theta θ,对于 θ i \theta_i θi,其更新表达式如下。更新完后继续回到步骤1: θ i = θ i − α 1 m ∑ j = 0 m ( h θ ( x 0 ( j ) , x 1 ( j ) , . . . x n ( j ) ) − y j ) x i ( j ) \theta_i=\theta_i-\alpha\frac{1}{m}\sum\limits_{j=0}^m(h_\theta(x_0^{(j)},x_1^{(j)},...x_n^{(j)})-y_j)x_i^{(j)} θi=θi−αm1j=0∑m(hθ(x0(j),x1(j),...xn(j))−yj)xi(j)
下面用线性回归的例子来具体描述梯度下降。
-
假设我们的样本是: ( x 1 ( 0 ) , x 2 ( 0 ) , . . . x n ( 0 ) , y 0 ) , ( x 1 ( 1 ) , x 2 ( 1 ) , . . . x n ( 1 ) , y 1 ) , . . . ( x 1 ( m ) , x 2 ( m ) , . . . x n ( m ) , y m ) (x^{(0)}_1,x^{(0)}_2,...x^{(0)}_n,y_0),(x^{(1)}_1,x^{(1)}_2,...x^{(1)}_n,y_1),...(x^{(m)}_1,x^{(m)}_2,...x^{(m)}_n,y_m) (x1(0),x2(0),...xn(0),y0),(x1(1),x2(1),...xn(1),y1),...(x1(m),x2(m),...xn(m),ym)
-
损失函数如前面先决条件所述: J ( θ 0 , θ 1 . . . , θ n ) = 1 2 m ∑ j = 0 m ( h θ ( x 0 ( j ) , x 1 ( j ) , . . . x n ( j ) ) − y j ) x i ( j ) J(\theta_0,\theta_1...,\theta_n)=\frac{1}{2m}\sum\limits_{j=0}^m(h_\theta(x_0^{(j)},x_1^{(j)},...x_n^{(j)})-y_j)x_i^{(j)} J(θ0,θ1...,θn)=2m1j=0∑m(hθ(x0(j),x1(j),...xn(j))−yj)xi(j)
-
则在推导过程中步骤1对于 θ i \theta_i θi的偏导数计算如下: σ σ θ i J ( θ 0 , θ 1 . . . , θ n ) = 1 m ∑ j = 0 m ( h θ ( x 0 ( j ) , x 1 ( j ) , . . . x n ( j ) ) − y j ) x i ( j ) \frac{\sigma}{\sigma\theta_i}J(\theta_0,\theta_1...,\theta_n)=\frac{1}{m}\sum\limits_{j=0}^m(h_\theta(x_0^{(j)},x_1^{(j)},...x_n^{(j)})-y_j)x_i^{(j)} σθiσJ(θ0,θ1...,θn)=m1j=0∑m(hθ(x0(j),x1(j),...xn(j))−yj)xi(j)
由于样本中没有 x 0 x_0 x0,所以上面的式子令所有 x 0 j x_0^j x0j 为1,所以步骤4、持续推导中的公式进行更新,如下: θ i = θ i − α 1 m ∑ j = 0 m ( h θ ( x 0 ( j ) , x 1 ( j ) , . . . x n ( j ) ) − y j ) x i ( j ) \theta_i=\theta_i-\alpha\frac{1}{m}\sum\limits_{j=0}^m(h_\theta(x_0^{(j)},x_1^{(j)},...x_n^{(j)})-y_j)x_i^{(j)} θi=θi−αm1j=0∑m(hθ(x0(j),x1(j),...xn(j))−yj)xi(j)
从这个例⼦可以看出当前点的梯度⽅向是由所有的样本决定的,加 1 m \frac{1}{m} m1是为了好理解。由于步⻓也为常数,他们的乘积也为常数,所以这⾥α 可以⽤⼀个常数表示。
5.2 梯度下降法家族
⾸先,我们来看⼀下,常⻅的梯度下降算法有:
-
全梯度下降算法(Full gradient descent)
-
随机梯度下降算法(Stochastic gradient descent),
-
⼩批量梯度下降算法(Mini-batch gradient descent),
-
随机平均梯度下降算法(Stochastic average gradient descent)
它们都是为了正确地调节权重向量,通过为每个权重计算⼀个梯度,从⽽更新权值,使⽬标函数尽可能最⼩化。其差别
在于样本的使⽤⽅式不同。
全梯度下降算法(FG)
这是梯度下降法最常⽤的形式,具体做法也就是在更新参数时使⽤所有的样本来进⾏更新。计算训练集所有样本误差,对其求和再取平均值作为⽬标函数。权重向量沿其梯度相反的⽅向移动,从⽽使当前⽬标函数减少得最多。
注意:
-
因为在执⾏每次更新时,我们需要在整个数据集上计算所有的梯度,所以速度会很慢,且⽆法处理超出内存容量限制的数据集。
-
全梯度下降法同样也不能在线更新模型,即在运⾏的过程中,不能增加新的样本。
随机梯度下降算法(SG)
由于FG每迭代更新⼀次权重都需要计算所有样本误差,⽽实际问题中经常有上亿的训练样本,故效率偏低,且容易陷⼊局部最优解,因此提出了随机梯度下降算法。
其每轮计算的⽬标函数不再是全体样本误差,⽽仅是单个样本误差,即每次只代⼊计算⼀个样本⽬标函数的梯度来更新权重,再取下⼀个样本重复此过程,直到损失函数值停⽌下降或损失函数值⼩于某个可以容忍的阈值。
此过程简单,⾼效,通常可以较好地避免更新迭代收敛到局部最优解。
注意:由于SG每次只使⽤⼀个样本迭代,若遇上噪声则容易陷⼊局部最优解。
⼩批量梯度下降算法(Mini-Batch)
⼩批量梯度下降算法是FG和SG的折中⽅案,在⼀定程度上兼顾了以上两种⽅法的优点。
每次从训练样本集上随机抽取⼀个⼩样本集,在抽出来的⼩样本集上采⽤FG迭代更新权重。
被抽出的⼩样本集所含样本点的个数称为batch_size,通常设置为2的幂次⽅,更有利于GPU加速处理(因为计算机是二进制)。
注意:若batch_size=1,则变成了SG算法;若batch_size=n,则变成了FG算法。
随机平均梯度下降算法(SAG)
在SG⽅法中,虽然避开了运算成本⼤的问题,但对于⼤数据训练⽽⾔,SG效果常不尽如⼈意,因为每⼀轮梯度更新都完全与上⼀轮的数据和梯度⽆关。
随机平均梯度算法克服了这个问题,在内存中为每⼀个样本都维护⼀个旧的梯度,随机选择第i个样本来更新此样本的梯度,其他样本的梯度保持不变,然后求得所有梯度的平均值,进⽽更新了参数。
如此,每⼀轮更新仅需计算⼀个样本的梯度,计算成本等同于SG,但收敛速度快得多。
6 线性回归API详解
正规方程API(之前初步使用的也是这个):sklearn.linear_model.LinearRegression(fit_intercept=True)
- fit_intercept:是否计算偏置。例如 y = k x + b y=kx+b y=kx+b,k就是回归系数,b就是偏置
- 返回对象的属性
- coef_:回归系数
- intercept:偏置
梯度下降API:sklearn.linear_model.SGDRegressor(loss="squared_loss", fit_intercept=True, learning_rate ='invscaling', eta0=0.01)
-
loss:损失函数,默认是普通最小二乘法squared_loss
-
fit_intercept:是否计算偏置
-
learning_rate:学习率的模式,通常直接默认就好。(改变这个参数可以影响到最终模型评估结果)
- “constant”:如果选这个,就需要指定eta=常数,来设置学习率
- “optimal”:eta = 1.0 / (alpha * (t + t0))
- “invscaling”: eta = eta0 / pow(t, power_t)
-
max_iter:最大迭代次数。为了避免一直迭代,可以设置这个参数。
-
返回对象属性
- conf_:回归系数
- intercept:偏置
7 案例:波士顿房价预测
7.1 数据集介绍
该数据集依然是来自sklearn,所以我们直接导入加载就好,下面是数据集的信息:
给定的这些特征,是专家们得出的影响房价的结果属性。我们此阶段不需要⾃⼰去探究特征是否有⽤,只需要使⽤这些特征。到后⾯量化很多特征需要我们⾃⼰去寻找。
7.2 回归模型评估
对于回归的性能是使用均方根误差(MSE,Mean Squared Error): M S E = 1 m ∑ i = 1 m ( y i − y ˉ ) MSE=\frac{1}{m}\sum_{i=1}^m(y^i-\bar{y}) MSE=m1i=1∑m(yi−yˉ)
注: y i y^i yi是预测值, y ˉ \bar{y} yˉ是真实值
sklearn.metrics.mean_squared_error(y_true, y_pred)计算均方根误差回归损失
- y_true:真实值
- y_pred:预测值
- 返回值是浮点数结果
7.3 代码实现
# -*- coding = utf-8 -*-
# @Time : 2021/8/12 10:56 下午
# @Author : zcy
# @File : 2.price_predict.py
# @Software : PyCharm
"""
波士顿房价预测——正规方程和梯度下降
"""
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression
from sklearn.linear_model import SGDRegressor
from sklearn.metrics import mean_squared_error
# 线性回归——正规方程
def linear_model1():
# 1.获取数据
boston = load_boston()
# 2.数据处理 —— 数据集划分
x_train, x_test, y_train, y_test = train_test_split(boston.data, boston.target, test_size=0.2, random_state=22)
# 3.特征工程 —— 特征预处理 标准化
transfer = StandardScaler()
x_train = transfer.fit_transform(x_train)
x_test = transfer.fit_transform(x_test)
# 4. 机器学习 —— 线性回归 正规方程
estimator = LinearRegression()
estimator.fit(x_train, y_train)
# 5. 模型评估
# 5.1 查看回归系数和偏置
y_predict = estimator.predict(x_test)
# print("预测值:\n", y_predict)
print("正规方程回归系数:", estimator.coef_)
print("偏置:", estimator.intercept_)
# 5.2 评估 均方根误差
print("均方根误差:", mean_squared_error(y_test, y_predict))
# 线性回归——梯度下降
def linear_model2():
# 1.获取数据
boston = load_boston()
# 2.数据处理 —— 数据集划分
x_train, x_test, y_train, y_test = train_test_split(boston.data, boston.target, test_size=0.2, random_state=22)
# 3.特征工程 —— 特征预处理 标准化
transfer = StandardScaler()
x_train = transfer.fit_transform(x_train)
x_test = transfer.fit_transform(x_test)
# 4. 机器学习 —— 线性回归 正规方程
estimator = SGDRegressor()
estimator.fit(x_train, y_train)
# 5. 模型评估
# 5.1 查看回归系数和偏置
y_predict = estimator.predict(x_test)
# print("预测值:\n", y_predict)
print("梯度下降回归系数:", estimator.coef_)
print("偏置:", estimator.intercept_)
# 5.2 评估 均方根误差
print("均方根误差:", mean_squared_error(y_test, y_predict))
linear_model1()
linear_model2()
可以发现,同等情况下,正规方程直接得到最好结果。
8 欠拟合和过拟合
8.1 定义
过拟合:⼀个假设在训练数据上能够获得⽐其他假设更好的拟合, 但是在测试数据集上却不能很好地拟合数据,此时认为这个假设出现了过拟合的现象。(简单的说,就是由于模型过于复杂,使模型得在训练集上表现好,而在测试集表现差)
欠拟合:⼀个假设在训练数据上不能获得更好的拟合,并且在测试数据集上也不能很好地拟合数据,此时认为这个假设出现了⽋拟合的现象。(即由于模型过于简单,在训练集和测试集上表现都差)
就像下图,欠拟合区域的测试误差和训练误差都很高,过拟合区域测试误差很高。
8.2 原因和解决方法
-
欠拟合
- 原因:模型学习时的数据特征太少
- 解决方法:
- 添加其他特征:既然特征不够,就添加新特征(可用"组合"、“泛化”、"相关性"等方式)。例如,我们想让机器识别一个物体是不是人,一开始人的特征只有“两只眼睛”、“一张嘴巴”、“一个鼻子”,但满足这个条件的也不一定是人,于是新增特征“能交流”。
- 添加多项式特征:这个在机器学习算法⾥⾯⽤的很普遍,例如将线性模型通过添加⼆次项或者三次项使模型泛化能⼒更强。
-
过拟合
- 原因:原始特征过多,存在⼀些嘈杂特征, 模型过于复杂是因为模型尝试去兼顾各个测试数据点。
- 解决方法:
- 重新清洗数据,导致过拟合的⼀个原因也有可能是数据不纯导致的,如果出现了过拟合就需要我们重新清洗数据。
- 增⼤数据的训练量,还有⼀个原因就是我们⽤于训练的数据量太⼩导致的,训练数据占总数据的⽐例过⼩。
- 正则化。(下一节介绍)
- 减少特征维度,防⽌维灾难。
8.3 正则化
正则化(或许称之为”约束化“更合理?)是用来解决过拟合的一种方法,其实就是对原有的一些异常特征进行限制(删除特征或者减小特征的影响)。例如下图过拟合的方程,之所以不符合要求,就是因为多了两个高次项 x 3 x^3 x3和 x 4 x^4 x4,我们可以将高次项的系数 θ 3 \theta_3 θ3和 θ 4 \theta_4 θ4设为零来删除 x 3 x^3 x3和 x 4 x^4 x4,也可以将它们设置非常小的数来减少 x 3 x^3 x3和 x 4 x^4 x4影响。
根据上面的描述,正则化可以分为两个类别:L1正则化和L2正则化。
- L1正则化(Lasso回归):使得权值向量 w w w直接为零(这里 w w w就是图上的 θ 3 \theta_3 θ3和 θ 4 \theta_4 θ4, w w w是损失函数里的权值),从而删除某特征的影响。
- L2正则化(Ridge回归,也称岭回归):
- 使得 w w w很小,趋近于零,从而大大削弱某特征的影响
- 这种方式更好,因为有些特征的影响是有必要存在的。
9 正则化线性模型
9.1 岭回归
岭回归是线性回归的正则化版本,它在原来的线性回归的损失函数中添加了一个正则项: α ∑ i = 1 n θ i 2 \alpha\sum\limits_{i=1}^n\theta^2_i αi=1∑nθi2。
就是把系数添加平⽅项,然后限制系数值的⼤⼩,α值越⼩,系数值 θ i \theta_i θi越⼤,α越⼤,系数值 θ i \theta_i θi越⼩。因为 J ( θ ) J(\theta) J(θ)和 M E S ( θ ) MES(\theta) MES(θ)是固定值,所以 α \alpha α和 θ i \theta_i θi就相互限制。当 α = 0 \alpha=0 α=0时,岭回归就退化为线性回归了。
所以,岭回归的损失函数为: J ( θ ) = M E S ( θ ) + α ∑ i = 1 n θ i 2 = 1 m ∑ i = 1 m ( θ T ⋅ x ( i ) − y ( i ) ) 2 + α ∑ i = 1 n θ i 2 J(\theta)=MES(\theta)+\alpha\sum\limits_{i=1}^n\theta^2_i=\frac{1}{m}\sum\limits_{i=1}^m(\theta^T \cdot x^{(i)}-y^{(i)})^2+\alpha\sum\limits_{i=1}^n\theta^2_i J(θ)=MES(θ)+αi=1∑nθi2=m1i=1∑m(θT⋅x(i)−y(i))2+αi=1∑nθi2
9.2 Lasso回归
Lasso 回归也是线性回归的另⼀种正则化版本,它在原本线性回归的损失函数中添加了正则项: α ∑ i = 1 n ∣ θ i ∣ \alpha\sum\limits_{i=1}^n \mid \theta_i \mid αi=1∑n∣θi∣
由于有绝对值,所以该正则项在顶点处不可导,在计算过程中会产生很多零,最终会得到一个稀疏矩阵,所以这种方式倾向于完全消除不重要的权重。
Lasso回归的损失函数为: J ( θ ) = M E S ( θ ) + α ∑ i = 1 n ∣ θ i ∣ J(\theta)=MES(\theta)+\alpha\sum\limits_{i=1}^n \mid \theta_i \mid J(θ)=MES(θ)+αi=1∑n∣θi∣
Lasso(alpha=1.0, fit_intercept=True, normalize=False, precompute=False, copy_X=True, max_iter=1000, tol=0.0001, warm_start=False, positive=False, random_state=None, selection=‘cyclic’)
• alphas:指定 λ \lambda λ值,默认为1。
• fit_intercept:bool类型,是否需要拟合截距项,默认为True。
• normalize:bool类型,建模时是否对数据集做标准化处理,默认为False。
• precompute:bool类型,是否在建模前计算Gram矩阵提升运算速度,默认为False。
• copy_X:bool类型,是否复制自变量X的数值,默认为True。
• max_iter:指定模型的最大迭代次数。
• tol:指定模型收敛的阈值,默认为0.0001。
• warm_start:bool类型,是否将前一次训练结果用作后一次的训练,默认为False。
• positive:bool类型,是否将回归系数强制为正数,默认为False。
• random_state:指定随机生成器的种子。
• selection:指定每次迭代选择的回归系数,如果为’random’,表示每次迭代中将随机更新回归系数;如果为’cyclic’,则每次迭代时回归系数的更新都基于上一次运算。
9.3 弹性网络(Elastic Net)
弹性⽹络在岭回归和Lasso回归中进⾏了折中,通过混合⽐**(mix ratio) r** 进⾏控制:
- r=0:弹性⽹络变为岭回归
- r=1:弹性⽹络便为Lasso回归
其损失函数为: J ( θ ) = M E S ( θ ) + r α ∑ i = 1 n ∣ θ i ∣ + 1 − r 2 α ∑ i = 1 n θ i 2 J(\theta)=MES(\theta)+r\alpha\sum\limits_{i=1}^n \mid \theta_i \mid+\frac{1-r}{2}\alpha\sum\limits_{i=1}^n\theta_i^2 J(θ)=MES(θ)+rαi=1∑n∣θi∣+21−rαi=1∑nθi2
9.4 小结-如何选择正则化方法?
-
通常⽤的是岭回归
-
当只有少部分特征有用时选择弹性网络和Lasso
- ⼀般来说,弹性⽹络的使⽤更为⼴泛。因为在特征维度⾼于训练样本数,或者特征是强相关的情况下,Lasso回归的表现不太稳定。
from sklearn.linear_model import Ridge, ElasticNet, Lasso
小结
-
Ridge Regression 岭回归
- 就是把系数添加平⽅项
- 然后限制系数值的⼤⼩
- α值越⼩,系数值越⼤,α越⼤,系数值越⼩
-
Lasso 回归
- 对系数值进⾏绝对值处理
- 由于绝对值在顶点处不可导,所以进⾏计算的过程中产⽣很多0,最后得到结果为:稀疏矩阵
-
Elastic Net 弹性⽹络
- 是前两个内容的综合
- 设置了⼀个r,如果r=0–岭回归;r=1–Lasso回归
-
Early stopping (了解即可)
- 通过限制错误率的阈值,进⾏停⽌
11 波士顿房价预测—岭回归
这些API用起来其实和前面差不多,只有细微区别,这里就用岭回归举例吧。
sklearn.linear_model.Ridge(alpha=1.0, fit_intercept=True,solver="auto", normalize=False)
- alpha:正则化力度,取值[0, 1]或者[1, 10]。用来控制权重系数的。alpha越大,权重系数越小。
- solver:选择优化算法,"auto"表示自动选择,通常默认就好。
- “sag”,也就是前面梯度下降法家族里的随机平均梯度下降。
- “svd”,使用X的奇异值分解来计算Ridge系数。对于奇异矩阵比cholesky更稳定。
- “cholesky”,使用标准的scipy.linalg.solve函数来获得闭合形式的解。
- “sparse_cg”,使用在scipy.sparse.linalg.cg中找到的共轭梯度求解器。作为迭代算法,这个求解器比大规模数据的cholesky更合适。
- “lsqr”,使用专用的正则化最小二乘常数scipy.sparse.linalg.lsqr。它是最快的,但可能在旧的scipy版本不可用。它是使用迭代过程。
- normalize:是否在回归前先进行归一化,默认为False。 当fit_intercept设置为False时,将忽略此参数。当回归量归一化时,注意到这使得超参数学习更加鲁棒,并且几乎不依赖于样本的数量。如果想标准化,可以在调用normalize = False训练估计器之前,使用StandardScaler()处理数据。
- 返回对象的属性
- coef_:回归权重(回归系数)
- Intercept_:回归偏置
其实Ridge()相当于前面的梯度下降SGDRegressor(penalty='l2', loss="squared_loss"),但梯度下降是SG,而岭回归是SAG。
sklearn.linear_model.RidgeCV(_BaseRidgeCV, RegressorMixin)是带有交叉验证的线性回归,我们可以传入多个alpha来找最好的参数。
# 线性回归——岭回归
def linear_model3():
# 1.获取数据
boston = load_boston()
# 2.数据处理 —— 数据集划分
x_train, x_test, y_train, y_test = train_test_split(boston.data, boston.target, test_size=0.2, random_state=22)
# 3.特征工程 —— 特征预处理 标准化
transfer = StandardScaler()
x_train = transfer.fit_transform(x_train)
x_test = transfer.fit_transform(x_test)
# 4. 机器学习 —— 线性回归 岭回归
estimator = RidgeCV(alphas=[1, 0.01, 0.05, 5])
estimator.fit(x_train, y_train)
# 5. 模型评估
# 5.1 查看回归系数和偏置
y_predict = estimator.predict(x_test)
# print("预测值:\n", y_predict)
# print("岭回归系数:", estimator.coef_)
# print("偏置:", estimator.intercept_)
# 5.2 评估 均方根误差
print("岭回归 均方根误差:", mean_squared_error(y_test, y_predict))
12 模型的保存和加载
需要导入joblib,保存模型用joblib.dump(estimator, 'test.pkl'),加载模型用estimator = joblib.load('test.pkl')
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import Ridge
from sklearn.metrics import mean_squared_error
import joblib
# 线性回归——岭回归 模型保存和加载
def linear_model3():
# 1.获取数据
boston = load_boston()
# 2.数据处理 —— 数据集划分
x_train, x_test, y_train, y_test = train_test_split(boston.data, boston.target, test_size=0.2, random_state=22)
# 3.特征工程 —— 特征预处理 标准化
transfer = StandardScaler()
x_train = transfer.fit_transform(x_train)
x_test = transfer.fit_transform(x_test)
# 4. 机器学习 —— 线性回归 岭回归
# 4.1 模型训练
# estimator = Ridge()
# estimator.fit(x_train, y_train)
#
# # 4.2 保存模型
# joblib.dump(estimator, "model.pkl")
# 4.3 加载模型
estimator = joblib.load("model.pkl")
# 5. 模型评估
# 5.1 查看回归系数和偏置
y_predict = estimator.predict(x_test)
# print("预测值:\n", y_predict)
# print("岭回归系数:", estimator.coef_)
# print("偏置:", estimator.intercept_)
# 5.2 评估 均方根误差
print("岭回归 均方根误差:", mean_squared_error(y_test, y_predict))
linear_model3()