匈牙利匹配算法_学习笔记_Python编程实现
大家好，下面是我关于匈牙利匹配算法的学习记录，内含两个例题的Python编程实现。这是我的第一篇博客，参考的网站在文中都有标注，如有问题欢迎指出~
匈牙利匹配算法
- 匈牙利算法1——无权重二部图最大匹配
-
- 几个概念
- 算法核心思想
- 算法理论依据
- 算法伪代码
- 算法复杂度
- 算法练习题1
- Python算法实现
- 匈牙利算法2——有权值二部图最小权值匹配
-
- 算法依据
- 算法思路
- 问题举例
- 算法流程
- 算法练习题2
- Python算法实现
匈牙利算法1——无权重二部图最大匹配
用于解决无权重二部图最大匹配问题，一个经典的解决无权重二分图的最大匹配问题的算法。
应用：机器人路径规划，群体智能（group intelligence）
几个概念
- 匹配：节点之间的连接关系；
- 二分图：节点被分为两类的图，不同类之间能够相互匹配，同类之间不能匹配，且每个节点最多仅能与一个其他节点匹配；
- 最大匹配：二分图所有匹配可能性中，匹配对数最多的情况；
- 完美匹配：所有节点都得到匹配（完美匹配一定是最大匹配）；
- 交替路：未匹配边->匹配边->未匹配边……交替的路；
- 增广路：是一个交替路，且非匹配边比匹配边多一条；
- 交替树：选一个空闲节点（树根）出发，遍历所有可能的交替路，构成交替树。
算法核心思想
如果把增广路中的匹配边和非匹配边相互调换，匹配边就比原来多一条。
算法理论依据
Berge’s Theorem: A matching M is maximun if it has no augmenting path.
Berge 定理：如果匹配 M 没有增广路径，则它是最大的（匹配）。
来自论文《The Hungarian Method 》1955，Naval Research Logistic Quarterly
算法伪代码
Given a bipartite graph G = ((X U Y),E)
for every v in x
{
if v is free
{
Find an augmenting path p start from v
if p is not empty
switch the edges in the path
}
}
解释说明：
以上算法可以用下图举例说明：
不断重复以上Step2和Step3:
算法复杂度
找节点v出发的增广路（可用广度优先BFS或深度优先DFS）复杂度：O(E)
外层循环V次
总复杂度：VO(E)
算法练习题1
要求：用匈牙利算法1实现求解下图的最大匹配的过程
上图可转化为如下二部图：
手动算法实现：
绿色表示未匹配边与节点，橙色表示匹配边与节点
Python算法实现
参考链接: https://blog.csdn.net/ying86615791/article/details/117735977
Python源程序：
# N和M分别代表左右边节点的个数,
# edges代表节点之间的连线：(右边节点，左边节点)
# graph是N*M矩阵, 记录左右节点之间是否存在连线
N = 4
M = 4
edges = [(0,0), (0,1), (0,2), (1,2), (2,0), (2,3), (3,3)]
graph = []
for i in range(N):
graph.append([])
for j in range(M):
if (i, j) in edges:
graph[i].append(1)
else:
graph[i].append(0)
# print("初始图: ")
# for i in range(N):
# print(graph[i])
# print("")
def find(x, graph, match, used):
# x (int): 当前尝试配对的左节点索引
# graph (list[list]): [N[M]], 是N*M矩阵, 记录左右节点之间是否存在连线
# match (list[int]): [M], 记录右节点被分配给坐标哪个节点
# used (list[int]): [M], 记录在本轮配对中某个右节点是否已经被访问过,
# 因为每一轮每个右节点只能被访问一次, 否则会被重复配对
for j in range(M):
# x和j是存在连线 and (j在本轮还没被访问过)
if graph[x][j] == 1 and not used[j]:
used[j] = True
# j还没被分配 or 成功把j腾出来(通过递归, 给j之前分配的左节点成功分配了另外1个右节点)
if match[j] == -1 or find(match[j], graph, match, used):
match[j] = x
return True
return False
# match记录左边节点最终与左边哪个节点匹配
match = [-1 for _ in range(M)]
# count记录最终的匹配数
count = 0
# # 遍历左节点, 依次尝试配对左边每个节点,
# 对于每次尝试配对的左节点,
# 如果能在右边找到与之匹配的右节点
# 则匹配数+1
for i in range(N):
# 每一轮是一次全新的查找, 所以used要重置,
# 但是是基于前面几轮找到的最优匹配, 所以match是复用的
used = [False for _ in range(M)]
if find(i, graph, match, used):
count += 1
#将节点序号转化为节点编号
num = []
for i in range(M):
num.append([])
if match[i] == 0:
num[i] = 5
elif match[i] == 1:
num[i] = 6
elif match[i] == 2:
num[i] = 7
elif match[i] == 3:
num[i] =8
else:
num[i]=-1
print("最大匹配个数: ", count)
print("左节点匹配到的右节点序号: ", num)
输出结果为：
与推导结果一致。
匈牙利算法2——有权值二部图最小权值匹配
解决有权值二部图最小权值匹配问题的算法。
应用：运动对象轨迹追踪（把视频分成帧，不同帧之间根据相似度对像素加权，跟踪同一个物体）
算法依据
定理1：如果在成本矩阵的任何一行或一列的所有条目上加或减一个数，则所得的成本矩阵的最优分配也是原始成本矩阵的最优分配。
定理2：当一个非负矩阵有代价为零的分配，则该分配就是一个最佳分配。
算法思路
通过对行和列的加减运算，将原矩阵变换为一个非负矩阵，方便找到最佳分配。
问题举例
-
已知
（1）完成一项工作需要4道工序；
（2）有5个工人（w1-w5），每人完成每道工序需要的时间不同 -
选择哪四个人，以及分配哪个人干哪个工序，才能使完成工作所需总时间最短？
算法流程
-
step1：转化为方阵，少的行/列用最大值填充；
-
step2：找出每行最小元素值，每行所有元素分别减去本行最小值；
-
step3：找出所有列中最小元素，每列减去本列最小值；
-
step4：用最少的直线覆盖矩阵中的全部0元素。如果直线数量等于矩阵行数（秩），则调到step6，否则，从没被线划过的元素中找到最小值x，然后矩阵中每次被线划过都增加x（划过n次则+nx），如下图所示；
此操作仍满足定理1 -
step5：从矩阵全部元素中找最小值n，所有元素均减去n，如下图所示：
-
重复step4和step5，知道满足结束条件，调到step6
-
step6：最终，选出M个0，每个0在不同行不同列
整体流程总结如下：
算法练习题2
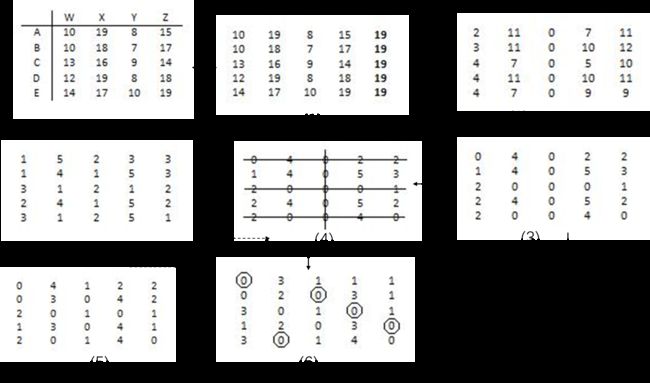
广告平台在不同时间段投放不同广告的收益不同，如下表。如果每个广告只能选择一个时间段，一个时间段只能播一个广告，怎么匹配广告和时间段才能最大化广告平台的收益？
上表的值用最大值19减去每一个值，可以将问题转化为有权值二部图最小权值匹配问题，转化后表格如下：
利用匈牙利算法2的流程分析如下：
Python算法实现
参考链接：https://blog.csdn.net/tommy0095/article/details/104466364
Python源代码如下：
import numpy as np
import collections
import time
class Hungarian():
def __init__(self, input_matrix=None, is_profit_matrix=False):
# is_profit_matrix=False代表输入是消费矩阵（需要使消费最小化），反之则为利益矩阵（需要使利益最大化）
if input_matrix is not None:
# 保存输入
my_matrix = np.array(input_matrix)
self._input_matrix = np.array(input_matrix)
self._maxColumn = my_matrix.shape[1]
self._maxRow = my_matrix.shape[0]
# 如果需要，则转化为消费矩阵
if is_profit_matrix:
my_matrix = self.make_cost_matrix(my_matrix)
self._cost_matrix = my_matrix
self._size = len(my_matrix)
self._shape = my_matrix.shape
# 存放算法结果
self._results = []
self._totalPotential = 0
else:
self._cost_matrix = None
def make_cost_matrix(self,profit_matrix):
# 利益矩阵转化为消费矩阵，输出为numpy矩阵
# 消费矩阵 = 利益矩阵最大值组成的矩阵 - 利益矩阵
matrix_shape = profit_matrix.shape
offset_matrix = np.ones(matrix_shape, dtype=int) * profit_matrix.max()
cost_matrix = offset_matrix - profit_matrix
return cost_matrix
def get_results(self):
# 获取算法结果
return self._results
def calculate(self):
# 实施匈牙利算法的函数
result_matrix = self._cost_matrix.copy()
# Step1: 矩阵每一行减去本行的最小值
for index, row in enumerate(result_matrix):
result_matrix[index] -= row.min()
# Step2: 矩阵每一列减去本行的最小值
for index, column in enumerate(result_matrix.T):
result_matrix[:, index] -= column.min()
# Step3： 使用最少数量的划线覆盖矩阵中所有的0元素
# 如果划线总数不等于矩阵的维度需要进行矩阵调整并重复循环此步骤
total_covered = 0
while total_covered < self._size:
# 使用最少数量的划线覆盖矩阵中所有的0元素同时记录划线数量
cover_zeros = CoverZeros(result_matrix)
single_zero_pos_list = cover_zeros.calculate()
covered_rows = cover_zeros.get_covered_rows()
covered_columns = cover_zeros.get_covered_columns()
total_covered = len(covered_rows) + len(covered_columns)
# 如果划线总数不等于矩阵的维度需要进行矩阵调整（需要使用未覆盖处的最小元素）
if total_covered < self._size:
result_matrix = self._adjust_matrix_by_min_uncovered_num(result_matrix, covered_rows, covered_columns)
#元组形式结果对存放到列表
self._results = single_zero_pos_list
# 计算总期望结果
value = 0
for row, column in single_zero_pos_list:
value += self._input_matrix[row, column]
self._totalPotential = value
def get_total_potential(self):
return self._totalPotential
def _adjust_matrix_by_min_uncovered_num(self, result_matrix, covered_rows, covered_columns):
# 计算未被覆盖元素中的最小值(m),未被覆盖元素减去最小值m,行列划线交叉处加上最小值m
adjusted_matrix = result_matrix
# 计算未被覆盖元素中的最小值（m）
elements = []
for row_index, row in enumerate(result_matrix):
if row_index not in covered_rows:
for index, element in enumerate(row):
if index not in covered_columns:
elements.append(element)
min_uncovered_num = min(elements)
#未被覆盖元素减去最小值m
for row_index, row in enumerate(result_matrix):
if row_index not in covered_rows:
for index, element in enumerate(row):
if index not in covered_columns:
adjusted_matrix[row_index,index] -= min_uncovered_num
#print('未被覆盖元素减去最小值m',adjusted_matrix)
#行列划线交叉处加上最小值m
for row_ in covered_rows:
for col_ in covered_columns:
adjusted_matrix[row_,col_] += min_uncovered_num
#print('行列划线交叉处加上最小值m',adjusted_matrix)
return adjusted_matrix
class CoverZeros():
# 使用最少数量的划线覆盖矩阵中的所有零
# 输入为numpy方阵
def __init__(self, matrix):
# 找到矩阵中零的位置（输出为同维度二值矩阵，0位置为true，非0位置为false）
self._zero_locations = (matrix == 0)
self._zero_locations_copy = self._zero_locations.copy()
self._shape = matrix.shape
# 存储划线盖住的行和列
self._covered_rows = []
self._covered_columns = []
def get_covered_rows(self):
# 返回覆盖行索引列表
return self._covered_rows
def get_covered_columns(self):
# 返回覆盖列索引列表
return self._covered_columns
def row_scan(self,marked_zeros):
# 扫描矩阵每一行，找到含0元素最少的行，对任意0元素标记（独立零元素），划去标记0元素（独立零元素）所在行和列存在的0元素
min_row_zero_nums = [9999999,-1]
for index, row in enumerate(self._zero_locations_copy):#index为行号
row_zero_nums = collections.Counter(row)[True]
if row_zero_nums < min_row_zero_nums[0] and row_zero_nums!=0:
#找最少0元素的行
min_row_zero_nums = [row_zero_nums,index]
#最少0元素的行
row_min = self._zero_locations_copy[min_row_zero_nums[1],:]
#找到此行中任意一个0元素的索引位置即可
row_indices, = np.where(row_min)
#标记该0元素
marked_zeros.append((min_row_zero_nums[1],row_indices[0]))
#划去该0元素所在行和列存在的0元素
#因为被覆盖，所以把二值矩阵_zero_locations中相应的行列全部置为false
self._zero_locations_copy[:,row_indices[0]] = np.array([False for _ in range(self._shape[0])])
self._zero_locations_copy[min_row_zero_nums[1],:] = np.array([False for _ in range(self._shape[0])])
def calculate(self):
# 进行计算
#储存勾选的行和列
ticked_row = []
ticked_col = []
marked_zeros = []
#1、试指派并标记独立零元素
while True:
#print('_zero_locations_copy',self._zero_locations_copy)
#循环直到所有零元素被处理（_zero_locations中没有true）
if True not in self._zero_locations_copy:
break
self.row_scan(marked_zeros)
#2、无被标记0（独立零元素）的行打勾
independent_zero_row_list = [pos[0] for pos in marked_zeros]
ticked_row = list(set(range(self._shape[0])) - set(independent_zero_row_list))
#重复3,4直到不能再打勾
TICK_FLAG = True
while TICK_FLAG:
#print('ticked_row:',ticked_row,' ticked_col:',ticked_col)
TICK_FLAG = False
#3、对打勾的行中所含0元素的列打勾
for row in ticked_row:
#找到此行
row_array = self._zero_locations[row,:]
#找到此行中0元素的索引位置
for i in range(len(row_array)):
if row_array[i] == True and i not in ticked_col:
ticked_col.append(i)
TICK_FLAG = True
#4、对打勾的列中所含独立0元素的行打勾
for row,col in marked_zeros:
if col in ticked_col and row not in ticked_row:
ticked_row.append(row)
FLAG = True
#对打勾的列和没有打勾的行画画线
self._covered_rows = list(set(range(self._shape[0])) - set(ticked_row))
self._covered_columns = ticked_col
return marked_zeros
if __name__ == '__main__':
cost_matrix = [
[9, 0, 8, 4],
[9, 1, 11, 2],
[6, 3, 9, 5],
[7, 0, 6, 1]]
hungarian = Hungarian(cost_matrix)
hungarian.calculate()
print("Calculated value:\t", hungarian.get_total_potential())
print("Results:\n\t", hungarian.get_results())
print("-" * 80)
profit_matrix = [
[10, 19, 11, 15],
[10, 18, 8, 17],
[13, 16, 10, 14],
[12, 19, 13, 18]]
hungarian = Hungarian(profit_matrix, is_profit_matrix=True)
hungarian.calculate()
print("Calculated value:\t", hungarian.get_total_potential())
print("Results:\n\t", hungarian.get_results())
输出结果为：
其中，第一个输出是将利益矩阵转化为成本矩阵后（转化方式如前所述），完全按照匈牙利算法求解的结果，最大利益应为19*4-14=62；
第二个输出是通过关系式“消费矩阵 = 利益矩阵最大值组成的矩阵 - 利益矩阵”转化，求解结果即为最大利益；
两个输出的匹配方式均与按算法流程推导的结果一致。
以上，如有问题欢迎指出~