【OpenCV--角点特征】

目录

一、什么是角点

二、Harris角点检测

1.原理：

 2.角点检测的实现：

 三、Shi-Tomasi角点检测

1.原理：

 2.实现：

---

一、什么是角点

1.举例：

 对于A-F六个小图找到原始图像中的位置：

A和B是平面，图像中很多地方存在，难以准确找到

C和D是边缘，可以近似确定其位置

E和F是角点，可以迅速确定位置

2.角点对图像理解、分析起着重要作用，在三维场景重建运动估计、目标跟踪、目标识别、图像配准与匹配起着重要作用，现实世界里，角点对应物体拐角，道路十字路口、丁字路口

二、Harris角点检测

1.原理：

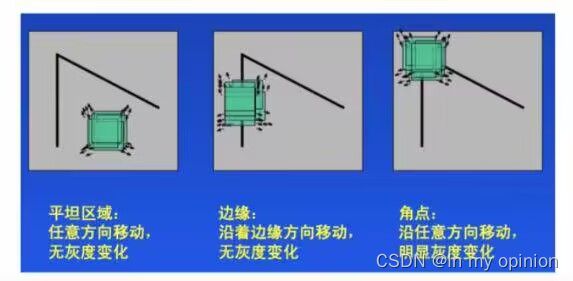
Harris角点检测是通过图像的局部小窗口观察图像，角点的特征是窗口沿着任意方向移动都会导致图像灰度的明显变化

转化为数学思想，将局部窗口向各个方向移动（u,v)并计算所有灰度差异总和,没有变化或比较小为平坦区域，表达式如下：E(u,v)= 
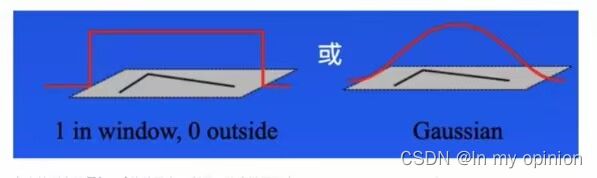
其中I(x, y)是局部窗口的图像灰度，I(x + u,y + v)是平移后的图像灰度，w(x, y)是窗口函数，该可以是矩形窗口，也可以是对每一个像素赋予不同权重的高斯窗口，如下所示:

 利用泰勒级数进行展开I(x+u，y+v)=I(x,y)++

 

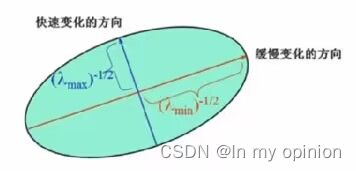
 M矩阵决定了E(x,y)的值，M是Ix和Iy的二次项函数，可以表示成椭圆的形状，椭圆的长短半轴由M的特征值入和决定,方向由特征矢量决定

 

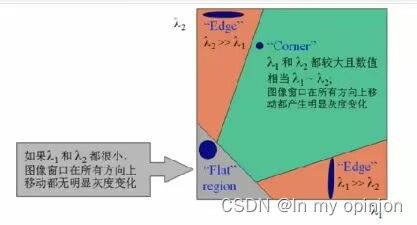
椭圆函数特征值与图像直线、角点、平面之间的关系：

1>图像中的直线：一个特征值大，另一个特征值小，λ1>>λ2或λ2>>λ1，椭圆函数值在某一方向上大，在其他方向上小
2>图像中的平面：两个特征值都小，且近似相等，椭圆函数数值在各个方向上都小。
3>图像中的角点：两个特征值都大，且近以相等，椭圆函数在所有方向都增大

Harris角点计算方法是通过计算一个角点响应值R来判断
R = detM - 
detM为矩阵M的行列式; traceM为矩阵M的迹; a为常数取值范围为0.04~0.06

detM=,traceM=

 2.角点检测的实现：

dst=cv.cornerHarris(src,blockSize,ksize,k)

参数：

src:数据类型为32的输入图像

blockSize:角点检测中需要考虑的邻域大小

k:角点检测中的自由参数，取值[0.04,0.06]

例：

import numpy as np
import matplotlib.pyplot as plt
import cv2 as cv
img=cv.imread('building.jpg')
gray=cv.cvtColor(img,cv.COLOR_BGR2GRAY)
#plt.imshow(img,cmap=plt.cm.gray)
#plt.show()
gray=np.float32(gray)
dst=cv.cornerHarris(gray,2,3,0.05)
img[dst>0.001*dst.max()]=[0,0,255]
plt.figure(figsize=(10,8),dpi=100)
plt.imshow(img[:,:,::])
plt.show()

 三、Shi-Tomasi角点检测

1.原理：

Shi-Tomasi算法一般会比Harris算法得到更好的角点，改进的方法是，若矩阵M的两个特征值中较小的一个大于阈值，则认为他是角点，即，R=min(，），从下图中可以看出和都大于最小值，被认为是角点

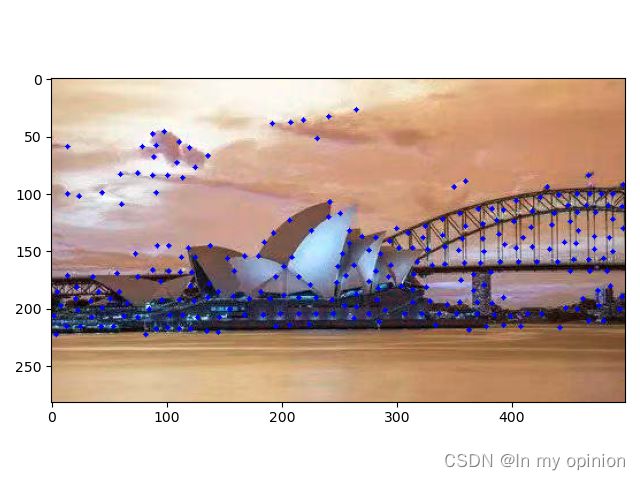
 2.实现：

corners=cv.goodFeaturesToTrack(image,maxCorners,qualityLevel,minDistance)

参数：

maxCorners:获取角点数的数目

quulityLevel:该参数指出最低可接受的角点质量水平，在0-1之间

minDistance:角点之间最小的欧氏距离，避免得到相邻特征点

import numpy as np
import matplotlib.pyplot as plt
import cv2 as cv
img=cv.imread('building.jpg')
gray=cv.cvtColor(img,cv.COLOR_BGR2GRAY)
corners=cv.goodFeaturesToTrack(gray,1000,0.01,10)
for i in corners:
    x,y=i.ravel()
    cv.circle(img,(int(x),int(y)),2,(0,0,255),-1)
plt.imshow(img[:,:,::])
plt.show()