基于飞蛾火焰优化算法的函数寻优算法

一、理论基础

飞蛾火焰优化算法(Moth-flame optimization algorithm, MFO)是一种新颖的群体智能算法，该算法由飞蛾和火焰两部分构成!通过横向定位导航机制来解决探索和开采之间的平衡问题。MFO具有参数简单、容易实现且鲁棒性好等优点，因此，自提出以来，便受到国内外学者的广泛关注，使其在诸多领域得到应用。

1、算法原理

（1）种群初始化

在MFO算法中，飞蛾个体为优化问题的候选解，飞蛾在优化空间的位置代表求解优化问题的变量，通过在优化空间中改变位置向量来向全局最佳点靠拢。MFO算法的种群$\mathbf{M}$由下列矩阵描述：$$\begin{array}{rl}& \mathbf{M}=[{\mathbf{m}}_1,{\mathbf{m}}_2,\cdots ,{\mathbf{m}}_n{]}^T\\ & {\mathbf{m}}_i=[m_{i,1},m_{i,2},\cdots ,m_{i,d}{]}^T\end{array}\text{\hspace{1em}(1)}$$其中，$n$为飞蛾数量，$d$为优化问题维数。飞蛾个体适应度值存储在$\mathbf{O}\mathbf{M}$矩阵中：$$\mathbf{O}\mathbf{M}=[O{M}_{1}O{M}_2\cdots O{M}_n{]}^T\text{\hspace{1em}(2)}$$火焰为当前迭代所获得的最佳位置，式(3)描述了最优位置矩阵$\mathbf{F}$，其适应度值存放在$\mathbf{O}\mathbf{F}$中。$$\begin{array}{rl}& \mathbf{F}=[{\mathbf{f}}_1,{\mathbf{f}}_2,\cdots ,{\mathbf{f}}_n{]}^T\\ & {\mathbf{f}}_i=[f_{i,1},f_{i,2},\cdots ,f_{i,d}{]}^T\end{array}\text{\hspace{1em}(3)}$$$$\mathbf{O}\mathbf{F}=[O{F}_{1}O{F}_2\cdots O{F}_n{]}^T\text{\hspace{1em}(4)}$$

（2）位置更新机制

受自然界飞蛾行为启发提出了MFO算法，飞蛾个体围绕在火焰周围迭代更新其位置直到搜索到最佳解决方案为止，其数学描述分为捕焰行为和弃焰行为。
（1）捕焰行为。自然界中具有趋光特性的飞蛾$M_i$会朝着距离自身最近的亮光(火焰)$F_j$移动。选择式(5)描述的对数螺线作为飞蛾捕焰的移动轨迹：$$S(M_i,F_j)=D_i\times e^{bt}\times \cos (2\pi t)+F_j\text{\hspace{1em}(5)}$$其中，$S(M_i,F_j)$为更新后的飞蛾位置；$b$为与螺线形状相关的常量；$t$为随机数，取值区间为$[-1,1]$，$t=-1$是最接近火焰，$t=1$是离火焰最远；$D_i=|F_j-M_i|$为飞蛾$M_i$到火焰$F_j$的距离。
（2） 弃焰行为。MFO算法通过弃焰行为自适应减少火焰数量，直到保持一个最优的火焰位置为止，火焰减少过程如式(6)所示：$$flame\_no=round(N-t\times \frac{N-1}{T})\text{\hspace{1em}(6)}$$其中，$t$和$T$分别为当前迭代次数和最大迭代次数；$N$为最大火焰数量。

2、算法步骤

飞蛾火焰优化算法的一般步骤如下：
步骤1 初始化算法参数：飞蛾数量$n$、维数$d$、最大迭代次数$T$等，随机初始化种群；
步骤2 计算种群中飞蛾的适应度值，并按适应度值进行升序排序；
步骤3 利用式(6)更新火焰数量；
步骤4 利用式(5)更新飞蛾位置；
步骤5 若满足给定的迭代次数!算法结束，获得最优解；否则，返回步骤2。

二、Matlab程序

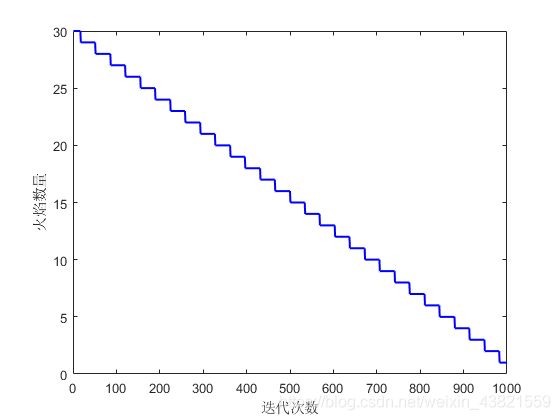
• 火焰数量自适应减少函数

%% 火焰自适应减少的数量
clear;
clc;

%% 
N = 30;          % 种群规模
T = 1000;        % 最大迭代次数

for t = 1:T
    flame_no(t) = round(N-t*(N-1)/T);
end

%%
figure;
plot(flame_no, 'b', 'linewidth', 1.5);
xlabel '迭代次数'; ylabel '火焰数量';

图1显示了火焰数量随迭代次数的增加而逐渐减少的事实。

图1 火焰自适应数量

• MFO算法主函数

function [Best_flame_score,Best_flame_pos,Convergence_curve]=MFO(N,Max_iteration,lb,ub,dim,fobj)

% 初始化飞蛾位置
Moth_pos = initialization(N, dim, ub, lb);

Convergence_curve = zeros(1, Max_iteration);

Iteration = 1;

%% 迭代
while Iteration < Max_iteration+1
    
    %% 弃焰行为
    % Eq. (3.14) in the paper--火焰自适应数量
    Flame_no = round(N-Iteration*((N-1)/Max_iteration));
    
    for i = 1:size(Moth_pos,1)
        % 边界处理
        Flag4ub = Moth_pos(i, :) > ub;
        Flag4lb = Moth_pos(i, :) < lb;
        Moth_pos(i, :) = (Moth_pos(i, :).*(~(Flag4ub+Flag4lb)))+ub.*Flag4ub+lb.*Flag4lb;
        % 计算适应度值
        Moth_fitness(i) = fobj(Moth_pos(i, :));
    end
    
    if Iteration == 1
        % 排序
        [fitness_sorted, I] = sort(Moth_fitness);
        sorted_population = Moth_pos(I, :);
        % 更新火焰
        best_flames = sorted_population;
        best_flame_fitness = fitness_sorted;
    else
        % 排序
        double_population = [previous_population; best_flames];
        double_fitness = [previous_fitness best_flame_fitness];
        
        [double_fitness_sorted,I] = sort(double_fitness);
        double_sorted_population = double_population(I, :);
        
        fitness_sorted = double_fitness_sorted(1:N);
        sorted_population = double_sorted_population(1:N, :);
        
        % 更新火焰
        best_flames = sorted_population;
        best_flame_fitness = fitness_sorted;
    end
    
    % 更新全局最优解
    Best_flame_score = fitness_sorted(1);
    Best_flame_pos = sorted_population(1,:);
    
    previous_population = Moth_pos;
    previous_fitness = Moth_fitness;
    
    %% 捕焰行为
    % a从-1到-2线性递减，以计算公式（3.12）中的t
    a = -1+Iteration*((-1)/Max_iteration);
    
    for i = 1:size(Moth_pos, 1)
        
        for j = 1:size(Moth_pos, 2)
            if i <= Flame_no        % 更新飞蛾相对于相应火焰的位置
                % D in Eq. (3.13)
                distance_to_flame = abs(sorted_population(i,j)-Moth_pos(i,j));
                b = 1;
                t = (a-1)*rand+1;
                % Eq. (3.12)
                Moth_pos(i, j) = distance_to_flame*exp(b.*t).*cos(t.*2*pi)+sorted_population(i, j);
            else                    % 更新飞蛾相对于相应火焰的位置
                % Eq. (3.13)
                distance_to_flame = abs(sorted_population(i, j)-Moth_pos(i, j));
                b = 1;
                t = (a-1)*rand+1;
                % Eq. (3.12)
                Moth_pos(i, j) = distance_to_flame*exp(b.*t).*cos(t.*2*pi)+sorted_population(Flame_no, j);
            end
        end
    end
    
    Convergence_curve(Iteration) = Best_flame_score;
    
    % 显示迭代信息
    display(['MFO:At iteration ', num2str(Iteration), ' the best fitness is ', num2str(Best_flame_score)]);
   
    Iteration = Iteration+1;
end

三、运行结果

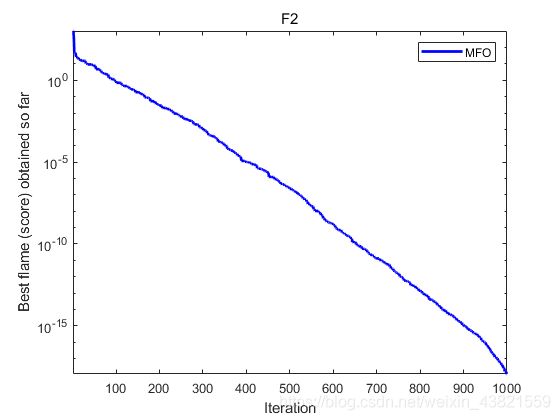
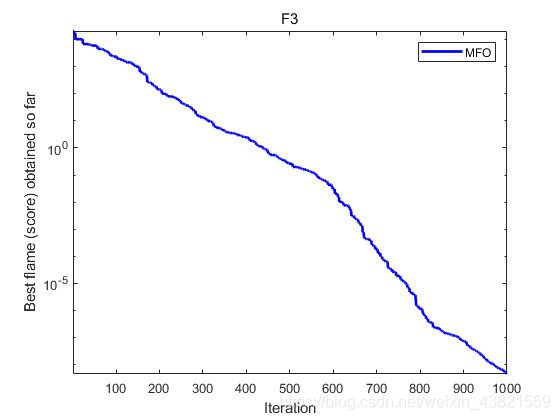
对文献[1]中的F1、F2、F3的10维函数进行测试，种群规模$N=30$，最大迭代次数$Max\_iteration=1000$，结果如下：

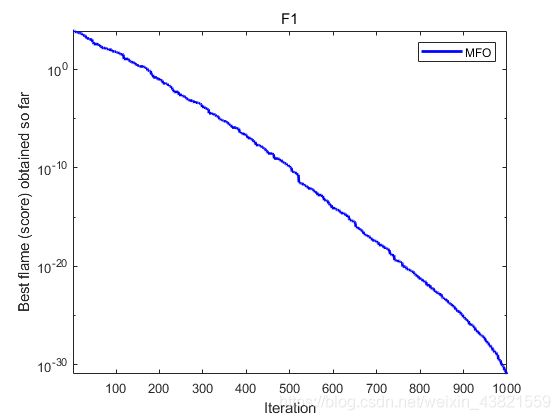
The best solution obtained by MFO is : -1.7505e-16  1.9705e-16 -1.2058e-16 -5.9773e-18  3.4731e-17  -6.391e-18 -4.2794e-17  6.2151e-17  1.1133e-16   1.135e-16
The best optimal value of the objective funciton found by MFO is : 1.1626e-31

The best solution obtained by MFO is : 8.2602e-20 -5.6014e-20 -6.5107e-20  1.1034e-19   1.239e-19  -7.165e-20  9.1319e-20 -2.1942e-19  9.8067e-20 -2.1097e-19
The best optimal value of the objective funciton found by MFO is : 1.1294e-18

The best solution obtained by MFO is : 4.2418e-05 -6.9891e-05  5.7333e-05 -3.0783e-05  5.1278e-06  9.7225e-06  1.0513e-05 -2.1992e-05 -1.4548e-05  8.8871e-06
The best optimal value of the objective funciton found by MFO is : 4.4182e-09

四、参考文献

[1] Mirjalili S. Moth-flame optimization algorithm: a novel nature- inspired heuristic paradigm[J]. Knowledge-Based Systems, 2015, 89: 228-249.
[2] 田鸿, 陈国彬, 刘超. 新型飞蛾火焰优化算法的研究[J]. 计算机工程与应用, 2019, 55(16): 138-143.
[3] 刘倩, 冯艳红, 陈嶷瑛. 基于混沌初始化和高斯变异的飞蛾火焰优化算法[J]. 郑州大学学报(工学版), 2021, 42(3): 53-58.