机器学习笔记之概率图模型(七)精确推断之变量消去法
机器学习笔记之概率图模型——精确推断之变量消去法
- 引言
-
- 回顾:推断的具体任务
- 变量消去法
-
- 基于有向图的变量消去法
- 基于无向图的变量消去法
- 变量消去法的弊端
- 关于复杂贝叶斯网络变量消去法的遗留问题
引言
上一节介绍了推断的本质以及推断的具体方法。本节将介绍精确推断方法中的变量消去法(Variable Elimination,VE)
回顾:推断的具体任务
推断(Inference)的任务本质上是求解变量或变量集合的概率结果。
已知样本集合 X \mathcal X X中的样本包含 p p p个特征。给定联合概率分布 P ( X ) = P ( x 1 , x 2 , ⋯ , x p ) \mathcal P(\mathcal X) = \mathcal P(x_1,x_2,\cdots,x_p) P(X)=P(x1,x2,⋯,xp)条件下:
- 某变量 x i ∈ { x 1 , ⋯ , x p } x_i \in \{x_1,\cdots,x_p\} xi∈{x1,⋯,xp}的边缘概率分布 可表示为:
概率的加法(积分)运算。
P ( x i ) = ∑ x 1 ⋯ ∑ x i − 1 ∑ x i + 1 ⋯ ∑ x p P ( x 1 , ⋯ , x p ) \mathcal P(x_i) = \sum_{x_1} \cdots \sum_{x_{i-1}}\sum_{x_{i+1}} \cdots \sum_{x_p} \mathcal P(x_1,\cdots,x_p) P(xi)=x1∑⋯xi−1∑xi+1∑⋯xp∑P(x1,⋯,xp) - 假设特征集合 X \mathcal X X被划分为两个子集合 x A , x B x_{\mathcal A},x_{\mathcal B} xA,xB,求解集合 x A x_{\mathcal A} xA的 x B x_{\mathcal B} xB条件下的概率分布 :
X = x A ∪ x B → P ( x A ∣ x B ) \mathcal X = x_{\mathcal A} \cup x_{\mathcal B} \to \mathcal P(x_{\mathcal A} \mid x_{\mathcal B}) X=xA∪xB→P(xA∣xB) - 最大后验概率推断(MAP Inference): x A x_{\mathcal A} xA集合的概率最优解 x A ^ \hat {x_{\mathcal A}} xA^与 条件概率 P ( x A ∣ x B ) \mathcal P(x_{\mathcal A} \mid x_{\mathcal B}) P(xA∣xB)和联合概率分布 P ( x A , x B ) \mathcal P(x_{\mathcal A},x_{\mathcal B}) P(xA,xB)之间的关系:
例如:隐马尔科夫模型中的‘解码问题’ -> Viterbi算法。
x A ^ = arg max x A P ( x A ∣ x B ) ∝ arg max x A P ( x A , x B ) \hat {x_{\mathcal A}} = \mathop{\arg\max}\limits_{x_{\mathcal A}} \mathcal P(x_{\mathcal A} \mid x_{\mathcal B}) \propto \mathop{\arg\max}\limits_{x_{\mathcal A}} \mathcal P(x_{\mathcal A},x_{\mathcal B}) xA^=xAargmaxP(xA∣xB)∝xAargmaxP(xA,xB)
变量消去法
变量消去法是精确推断中最简单的推断方法,从名字中可以看出,该方法目的是消除条件中各种无关变量。
基于有向图的变量消去法
示例:已知一个简单概率图表示如下:
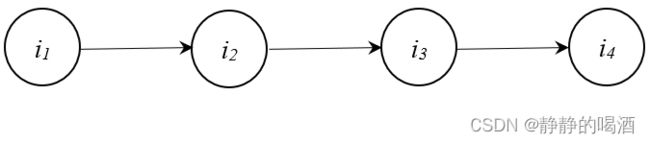
任务:求解节点 i 4 i_4 i4的概率分布 P ( i 4 ) \mathcal P(i_4) P(i4)。
-
根据概率的加法(积分)公式,使用联合概率分布 P ( i 1 , i 2 , i 3 , i 4 ) \mathcal P(i_1,i_2,i_3,i_4) P(i1,i2,i3,i4)对 P ( i 4 ) \mathcal P(i_4) P(i4)进行表示:
P ( i 4 ) = ∑ i 1 , i 2 , i 3 P ( i 1 , i 2 , i 3 , i 4 ) \mathcal P(i_4) = \sum_{i_1,i_2,i_3}\mathcal P(i_1,i_2,i_3,i_4) P(i4)=i1,i2,i3∑P(i1,i2,i3,i4) -
由于该图是有向图,因此直接使用贝叶斯网络的因子分解 对联合概率分布进行表示:
这里定义变量i 1 , i 2 , i 3 , i 4 i_1,i_2,i_3,i_4 i1,i2,i3,i4均是‘离散型随机变量’。
P ( i 1 , i 2 , i 3 , i 4 ) = ∏ k = 1 p P ( i k ∣ i p a ( k ) ) = P ( i 1 ) ⋅ P ( i 2 ∣ i 1 ) ⋅ P ( i 3 ∣ i 2 ) ⋅ P ( i 4 ∣ i 3 ) \begin{aligned} \mathcal P(i_1,i_2,i_3,i_4) & = \prod_{k=1}^p \mathcal P(i_k \mid i_{pa(k)})\\ & = \mathcal P(i_1) \cdot \mathcal P(i_2 \mid i_1) \cdot \mathcal P(i_3 \mid i_2) \cdot \mathcal P(i_4 \mid i_3) \end{aligned} P(i1,i2,i3,i4)=k=1∏pP(ik∣ipa(k))=P(i1)⋅P(i2∣i1)⋅P(i3∣i2)⋅P(i4∣i3)
最终,结点 i 4 i_4 i4的概率分布可表示为:
P ( i 4 ) = ∑ i 1 , i 2 , i 3 P ( i 1 ) ⋅ P ( i 2 ∣ i 1 ) ⋅ P ( i 3 ∣ i 2 ) ⋅ P ( i 4 ∣ i 3 ) \mathcal P(i_4) = \sum_{i_1,i_2,i_3}\mathcal P(i_1) \cdot \mathcal P(i_2 \mid i_1) \cdot \mathcal P(i_3 \mid i_2) \cdot \mathcal P(i_4 \mid i_3) P(i4)=i1,i2,i3∑P(i1)⋅P(i2∣i1)⋅P(i3∣i2)⋅P(i4∣i3) -
如果直接对 P ( i 4 ) \mathcal P(i_4) P(i4)进行求解,需要将上式展开。这里为简化运算,定义变量 i 1 , i 2 , i 3 , i 4 i_1,i_2,i_3,i_4 i1,i2,i3,i4均服从伯努利分布:
i 1 , i 2 , i 3 , i 4 ∈ { 0 , 1 } i_1,i_2,i_3,i_4 \in \{0,1\} i1,i2,i3,i4∈{0,1}
展开结果表示如下:
注意:这里只对i 1 , i 2 , i 3 i_1,i_2,i_3 i1,i2,i3进行积分,因此只有2 3 = 8 2^3 = 8 23=8项。
P ( i 4 ) = ∑ i 1 , i 2 , i 3 P ( i 1 ) ⋅ P ( i 2 ∣ i 1 ) ⋅ P ( i 3 ∣ i 2 ) ⋅ P ( i 4 ∣ i 3 ) = P ( i 1 = 0 ) ⋅ P ( i 2 = 0 ∣ i 1 = 0 ) ⋅ P ( i 3 = 0 ∣ i 2 = 0 ) ⋅ P ( i 4 ∣ i 3 = 0 ) + ⋯ + P ( i 1 = 1 ) ⋅ P ( i 2 = 1 ∣ i 1 = 1 ) ⋅ P ( i 3 = 1 ∣ i 2 = 1 ) ⋅ P ( i 4 ∣ i 3 = 1 ) \begin{aligned} \mathcal P(i_4) & = \sum_{i_1,i_2,i_3} \mathcal P(i_1) \cdot \mathcal P(i_2 \mid i_1) \cdot \mathcal P(i_3 \mid i_2) \cdot \mathcal P(i_4 \mid i_3) \\ & = \mathcal P(i_1 = 0) \cdot \mathcal P(i_2 = 0 \mid i_1 = 0) \cdot \mathcal P(i_3 = 0 \mid i_2 = 0) \cdot \mathcal P(i_4 \mid i_3 = 0) + \cdots + \\ & \mathcal P(i_1 = 1) \cdot \mathcal P(i_2 = 1 \mid i_1 = 1) \cdot \mathcal P(i_3 = 1 \mid i_2 = 1) \cdot \mathcal P(i_4 \mid i_3 = 1) \end{aligned} P(i4)=i1,i2,i3∑P(i1)⋅P(i2∣i1)⋅P(i3∣i2)⋅P(i4∣i3)=P(i1=0)⋅P(i2=0∣i1=0)⋅P(i3=0∣i2=0)⋅P(i4∣i3=0)+⋯+P(i1=1)⋅P(i2=1∣i1=1)⋅P(i3=1∣i2=1)⋅P(i4∣i3=1)
观察该结果,我们发现如下问题:
观察概率加法公式中的项数,即便是最简单的顺序结构,并且各变量均是最简单的伯努利分布,单每增加一个节点,项数依然会指数倍地增长。
很明显,真实情况中,概率图的结构只会更加复杂。因此,该算法的复杂度不小于 K p \mathcal K^p Kp。
其中K \mathcal K K表示基于节点分布的综合结果,可能每个节点的分布各不相同;p p p表示节点个数。 -
变量消除法的思想是:在图结构中,和某节点相关联的节点数量是有限的。在积分过程中,只将相关联的节点进行积分运算,不相关的节点,对应的因子直接视为常数即可。
继续观察 P ( i 4 ) \mathcal P(i_4) P(i4)的因子分解:
P ( i 4 ) = ∑ i 1 , i 2 , i 3 P ( i 1 ) ⋅ P ( i 2 ∣ i 1 ) ⋅ P ( i 3 ∣ i 2 ) ⋅ P ( i 4 ∣ i 3 ) \mathcal P(i_4) = \sum_{i_1,i_2,i_3} \mathcal P(i_1) \cdot \mathcal P(i_2 \mid i_1) \cdot \mathcal P(i_3 \mid i_2) \cdot \mathcal P(i_4 \mid i_3) P(i4)=i1,i2,i3∑P(i1)⋅P(i2∣i1)⋅P(i3∣i2)⋅P(i4∣i3)
上述4项因子结果中,和结点 i 1 i_1 i1无关的项有: P ( i 3 ∣ i 2 ) , P ( i 4 ∣ i 3 ) \mathcal P(i_3 \mid i_2),\mathcal P(i_4 \mid i_3) P(i3∣i2),P(i4∣i3)。
将因子分解表示为如下形式:
P ( i 4 ) = ∑ i 2 , i 3 P ( i 3 ∣ i 2 ) ⋅ P ( i 4 ∣ i 3 ) ⋅ ∑ i 1 P ( i 1 ) ⋅ P ( i 2 ∣ i 1 ) \begin{aligned} \mathcal P(i_4) & = \sum_{i_2,i_3} \mathcal P(i_3 \mid i_2) \cdot \mathcal P(i_4 \mid i_3) \cdot \sum_{i_1} \mathcal P(i_1) \cdot \mathcal P(i_2 \mid i_1) \end{aligned} P(i4)=i2,i3∑P(i3∣i2)⋅P(i4∣i3)⋅i1∑P(i1)⋅P(i2∣i1)
观察后项 ∑ i 1 P ( i 1 ) ⋅ P ( i 2 ∣ i 1 ) \sum_{i_1} \mathcal P(i_1) \cdot \mathcal P(i_2 \mid i_1) ∑i1P(i1)⋅P(i2∣i1)可表示如下:
‘概率密度积分’
∑ i 1 P ( i 1 ) ⋅ P ( i 2 ∣ i 1 ) = ∑ i 1 P ( i 1 , i 2 ) = P i 1 ( i 2 ) \begin{aligned} \sum_{i_1} \mathcal P(i_1) \cdot \mathcal P(i_2 \mid i_1) = \sum_{i_1} \mathcal P(i_1,i_2) = \mathcal P_{i_1}(i_2) \end{aligned} i1∑P(i1)⋅P(i2∣i1)=i1∑P(i1,i2)=Pi1(i2)
这里将上述积分结果定义一个符号: P i 1 ( i 2 ) \mathcal P_{i_1}(i_2) Pi1(i2),表示 i 2 i_2 i2的边缘概率 P i 1 ( i 2 ) \mathcal P_{i_1}(i_2) Pi1(i2)是通过对 i 1 i_1 i1进行积分得到的结果。
因此, P ( i 4 ) \mathcal P(i_4) P(i4)可表示如下:
P ( i 4 ) = ∑ i 2 , i 3 P ( i 3 ∣ i 2 ) ⋅ P ( i 4 ∣ i 3 ) ⋅ P i 1 ( i 2 ) = ∑ i 3 P ( i 4 ∣ i 3 ) ⋅ ∑ i 2 P ( i 3 ∣ i 2 ) ⋅ P i 1 ( i 2 ) \begin{aligned} \mathcal P(i_4) & = \sum_{i_2,i_3} \mathcal P(i_3 \mid i_2) \cdot \mathcal P(i_4 \mid i_3) \cdot \mathcal P_{i_1}(i_2) \\ & = \sum_{i_3} \mathcal P(i_4 \mid i_3) \cdot \sum_{i_2} \mathcal P(i_3 \mid i_2) \cdot \mathcal P_{i_1}(i_2) \end{aligned} P(i4)=i2,i3∑P(i3∣i2)⋅P(i4∣i3)⋅Pi1(i2)=i3∑P(i4∣i3)⋅i2∑P(i3∣i2)⋅Pi1(i2)
变量消除法的核心:继续观察后项: ∑ i 2 P ( i 3 ∣ i 2 ) ⋅ P i 1 ( i 2 ) \sum_{i_2} \mathcal P(i_3 \mid i_2) \cdot \mathcal P_{i_1}(i_2) ∑i2P(i3∣i2)⋅Pi1(i2),和上面的化简相同,可以继续使用概率密度积分 对该式进行化简:
∑ i 2 P ( i 3 ∣ i 2 ) ⋅ P i 1 ( i 2 ) = ∑ i 2 P ( i 2 , i 3 ) = P i 2 ( i 3 ) \sum_{i_2} \mathcal P(i_3 \mid i_2) \cdot \mathcal P_{i_1}(i_2) = \sum_{i_2} \mathcal P(i_2,i_3) = \mathcal P_{i_2}(i_3) i2∑P(i3∣i2)⋅Pi1(i2)=i2∑P(i2,i3)=Pi2(i3)
注意:这里i 2 i_2 i2的边缘概率P i 1 ( i 2 ) \mathcal P_{i_1}(i_2) Pi1(i2)是子集合{ i 1 , i 2 } \{i_1,i_2\} {i1,i2}中的边缘概率。也就是说,i 2 i_2 i2的边缘概率并没有对其他节点进行积分。但是结果是'完全相同'的。是因为在上述示例概率图中,只有结点i 1 i_1 i1指向了i 2 i_2 i2,其他节点与i 2 i_2 i2的边缘概率无关。即:P i 1 ( i 2 ) = ∑ i 1 P ( i 1 , i 2 ) = ∑ i 1 , i 3 , i 4 P ( i 1 , i 2 , i 3 , i 4 ) = P ( i 2 ) \mathcal P_{i_1}(i_2) = \sum_{i_1} \mathcal P(i_1,i_2) = \sum_{i_1,i_3,i_4} \mathcal P(i_1,i_2,i_3,i_4) = \mathcal P(i_2) Pi1(i2)=i1∑P(i1,i2)=i1,i3,i4∑P(i1,i2,i3,i4)=P(i2)
同理,最终可以将 P ( i 4 ) \mathcal P(i_4) P(i4)化简为:
P ( i 4 ) = ∑ i 3 P ( i 4 ∣ i 3 ) ⋅ P i 2 ( i 3 ) = P i 3 ( i 4 ) \mathcal P(i_4) = \sum_{i_3} \mathcal P(i_4 \mid i_3) \cdot \mathcal P_{i_2}(i_3) = \mathcal P_{i_3}(i_4) P(i4)=i3∑P(i4∣i3)⋅Pi2(i3)=Pi3(i4) -
将变量消去法与因子分解方法进行对比:
{ P ( i 4 ) = ∑ i 1 , i 2 , i 3 P ( i 1 ) ⋅ P ( i 2 ∣ i 1 ) ⋅ P ( i 3 ∣ i 2 ) ⋅ P ( i 4 ∣ i 3 ) P ( i 4 ) = ∑ i 3 P ( i 4 ∣ i 3 ) ⋅ ∑ i 2 P ( i 3 ∣ i 2 ) ⋅ ∑ i 1 P ( i 2 ∣ i 1 ) ⋅ P ( i 1 ) \begin{cases} \mathcal P(i_4) = \sum_{i_1,i_2,i_3} \mathcal P(i_1) \cdot \mathcal P(i_2 \mid i_1) \cdot \mathcal P(i_3 \mid i_2) \cdot \mathcal P(i_4 \mid i_3) \\ \mathcal P(i_4) = \sum_{i_3} \mathcal P(i_4 \mid i_3) \cdot \sum_{i_2} \mathcal P(i_3 \mid i_2) \cdot \sum_{i_1} \mathcal P(i_2\mid i_1) \cdot \mathcal P(i_1) \end{cases} {P(i4)=∑i1,i2,i3P(i1)⋅P(i2∣i1)⋅P(i3∣i2)⋅P(i4∣i3)P(i4)=∑i3P(i4∣i3)⋅∑i2P(i3∣i2)⋅∑i1P(i2∣i1)⋅P(i1)
发现变量消去法每次将求积和求和的运算限制在局部范围内,仅和部分变量相关,从而简化运算。
从运算过程角度,即‘乘法对加法的分配律’。
基于无向图的变量消去法
变量消去法并不是仅基于贝叶斯网络(有向图),马尔可夫随机场(无向图)同样可以使用该方法进行运算。不同于有向图节点之间显式的因果关系,无向图可以通过势函数来描述节点之间的关联关系:
某无向图模型表示如下:

目标:求解结点 i 4 i_4 i4的边缘概率结果 P ( i 4 ) \mathcal P(i_4) P(i4)。
- 首先观察该无向图中包含 3 3 3个极大团:
- { i 0 , i 1 } \{i_0,i_1\} {i0,i1}
- { i 1 , i 2 , i 3 } \{i_1,i_2,i_3\} {i1,i2,i3}
- { i 3 , i 4 } \{i_3,i_4\} {i3,i4}
- 基于极大团,使用势函数对无向图的联合概率分布 P ( i 0 , i 1 , i 2 , i 3 , i 4 ) \mathcal P(i_0,i_1,i_2,i_3,i_4) P(i0,i1,i2,i3,i4)表示如下:
P ( i 0 , i 1 , i 2 , i 3 , i 4 ) = 1 Z ψ 01 ( i 0 , i 1 ) ⋅ ψ 123 ( i 1 , i 2 , i 3 ) ⋅ ψ 34 ( i 3 , i 4 ) \mathcal P(i_0,i_1,i_2,i_3,i_4) = \frac{1}{\mathcal Z} \psi_{01}(i_0,i_1) \cdot \psi_{123}(i_1,i_2,i_3) \cdot \psi_{34}(i_3,i_4) P(i0,i1,i2,i3,i4)=Z1ψ01(i0,i1)⋅ψ123(i1,i2,i3)⋅ψ34(i3,i4) - 从而 P ( i 4 ) \mathcal P(i_4) P(i4)表示如下:
P ( i 4 ) = ∑ i 0 , ⋯ , i 3 P ( i 0 , i 1 , i 2 , i 3 , i 4 ) = 1 Z ∑ i − 0 , ⋯ , i 3 ψ 01 ( i 0 , i 1 ) ⋅ ψ 123 ( i 1 , i 2 , i 3 ) ⋅ ψ 34 ( i 3 , i 4 ) \begin{aligned} \mathcal P(i_4) & = \sum_{i_0,\cdots,i_3} \mathcal P(i_0,i_1,i_2,i_3,i_4) \\ & = \frac{1}{\mathcal Z}\sum_{i-0,\cdots,i_3} \psi_{01}(i_0,i_1) \cdot \psi_{123}(i_1,i_2,i_3) \cdot \psi_{34}(i_3,i_4) \end{aligned} P(i4)=i0,⋯,i3∑P(i0,i1,i2,i3,i4)=Z1i−0,⋯,i3∑ψ01(i0,i1)⋅ψ123(i1,i2,i3)⋅ψ34(i3,i4) - 使用变量消去法,从某一变量开始,沿着无向图的路径对变量进行依次消去:
与贝叶斯网络相对应,定义 ∑ i 0 ψ 01 ( i 0 , i 1 ) \sum_{i_0} \psi_{01}(i_0,i_1) ∑i0ψ01(i0,i1)对 i 0 i_0 i0积分后的函数结果,其结果是关于 i 1 i_1 i1的函数,记作 m 01 ( i 1 ) m_{01}(i_1) m01(i1),其他变量同理。
由于最大团{ i 1 , i 2 , i 3 } \{i_1,i_2,i_3\} {i1,i2,i3}包含3个变量,因此可以‘依次进行积分’(个人理解)。
公式中出现的m 1 → 23 ( i 2 , i 3 ) m_{1 \to 23}(i_2,i_3) m1→23(i2,i3)表示将i 1 i_1 i1积分掉后,关于变量i 2 , i 3 i_2,i_3 i2,i3的函数。
P ( i 4 ) = 1 Z ∑ i 1 , i 2 , i 3 ψ 123 ( i 1 , i 2 , i 3 ) ⋅ ψ 34 ( i 3 , i 4 ) ⋅ ∑ i 0 ψ 01 ( i 0 , i 1 ) = 1 Z ∑ i 2 , i 3 ψ 34 ( i 3 , i 4 ) ⋅ ∑ i 1 ψ 123 ( i 1 , i 2 , i 3 ) ⋅ m 01 ( i 1 ) = 1 Z ∑ i 3 ψ 34 ( i 3 , i 4 ) ⋅ ∑ i 2 m 1 → 23 ( i 2 , i 3 ) = 1 Z ∑ i 3 ψ 34 ( i 3 , i 4 ) ⋅ m 23 ( i 3 ) = 1 Z m 34 ( i 4 ) \begin{aligned} \mathcal P(i_4) & = \frac{1}{\mathcal Z}\sum_{i_1,i_2,i_3} \psi_{123}(i_1,i_2,i_3) \cdot \psi_{34}(i_3,i_4) \cdot \sum_{i_0} \psi_{01}(i_0,i_1) \\ & = \frac{1}{\mathcal Z} \sum_{i_2,i_3} \psi_{34}(i_3,i_4)\cdot \sum_{i_1} \psi_{123}(i_1,i_2,i_3) \cdot m_{01}(i_1) \\ & = \frac{1}{\mathcal Z} \sum_{i_3} \psi_{34}(i_3,i_4) \cdot \sum_{i_2}m_{1 \to 23}(i_2,i_3) \\ & = \frac{1}{\mathcal Z}\sum_{i_3} \psi_{34}(i_3,i_4) \cdot m_{23}(i_3) \\ & = \frac{1}{\mathcal Z} m_{34}(i_4) \end{aligned} P(i4)=Z1i1,i2,i3∑ψ123(i1,i2,i3)⋅ψ34(i3,i4)⋅i0∑ψ01(i0,i1)=Z1i2,i3∑ψ34(i3,i4)⋅i1∑ψ123(i1,i2,i3)⋅m01(i1)=Z1i3∑ψ34(i3,i4)⋅i2∑m1→23(i2,i3)=Z1i3∑ψ34(i3,i4)⋅m23(i3)=Z1m34(i4)
变量消去法的弊端
上述基于无向图的变量消去法,其变量的消去顺序为: i 0 , i 1 , i 2 , i 3 i_0,i_1,i_2,i_3 i0,i1,i2,i3,但在真实情况中,使用变量消去法,并非只有一种消去顺序。
例如贝叶斯网络,我们通常使用拓扑排序的方式选择消去顺序;由于图中 入度为零的变量节点 可能不止一个,并且拓扑排序过程中路径并非只有一条。因此理论上可以有多种顺序对变量节点进行消除;
那么若干种消除顺序,总会存在代价最小的一条,但是想要找到这条代价最小的顺序,这个行为本身的代价是极高的。会涉及 NP-Hard问题:如果想要找到代价最小的顺序,最坏情况下需要对每一个路径进行遍历,这个代价是极高的。
假设需要计算多个节点变量的边缘概率,如上图中,求解完 P ( i 4 ) \mathcal P(i_4) P(i4)后又需要求 P ( i 3 ) \mathcal P(i_3) P(i3),则需要执行 { i 0 , i 1 , i 2 } \{i_0,i_1,i_2\} {i0,i1,i2} 的顺序重头计算,这种操作的计算资源消耗是极高的。
关于复杂贝叶斯网络变量消去法的遗留问题
已知贝叶斯网络描述如下:

很明显,这是一个有向无环图,任务目标依旧是求解变量节点 i 4 i_4 i4的边缘概率分布 P ( i 4 ) \mathcal P(i_4) P(i4):
-
首先,该图的因子分解表示如下:
P ( i 0 , i 1 , i 2 , i 3 , i 4 ) = ∏ i = 0 4 P ( i k ∣ i p a ( k ) ) = P ( i 0 ) ⋅ P ( i 1 ∣ i 0 ) ⋅ P ( i 2 ∣ i 1 ) ⋅ P ( i 3 ∣ i 1 , i 2 ) ⋅ P ( i 4 ∣ i 3 ) \begin{aligned} \mathcal P(i_0,i_1,i_2,i_3,i_4) & = \prod_{i=0}^4 \mathcal P(i_k \mid i_{pa(k)}) \\ & = \mathcal P(i_0) \cdot \mathcal P(i_1 \mid i_0) \cdot \mathcal P(i_2 \mid i_1) \cdot \mathcal P(i_3 \mid i_1,i_2) \cdot \mathcal P(i_4 \mid i_3) \end{aligned} P(i0,i1,i2,i3,i4)=i=0∏4P(ik∣ipa(k))=P(i0)⋅P(i1∣i0)⋅P(i2∣i1)⋅P(i3∣i1,i2)⋅P(i4∣i3)
因而, P ( i 4 ) \mathcal P(i_4) P(i4)表示如下:
P ( i 4 ) = ∑ i 0 , i 1 , i 2 , i 3 P ( i 0 , i 1 , i 2 , i 3 , i 4 ) = ∑ i 0 , i 1 , i 2 , i 3 P ( i 0 ) ⋅ P ( i 1 ∣ i 0 ) ⋅ P ( i 2 ∣ i 1 ) ⋅ P ( i 3 ∣ i 1 , i 2 ) ⋅ P ( i 4 ∣ i 3 ) \mathcal P(i_4) = \sum_{i_0,i_1,i_2,i_3} \mathcal P(i_0,i_1,i_2,i_3,i_4) = \sum_{i_0,i_1,i_2,i_3} \mathcal P(i_0) \cdot \mathcal P(i_1 \mid i_0) \cdot \mathcal P(i_2 \mid i_1) \cdot \mathcal P(i_3 \mid i_1,i_2) \cdot \mathcal P(i_4 \mid i_3) P(i4)=i0,i1,i2,i3∑P(i0,i1,i2,i3,i4)=i0,i1,i2,i3∑P(i0)⋅P(i1∣i0)⋅P(i2∣i1)⋅P(i3∣i1,i2)⋅P(i4∣i3) -
第一步:消去变量 i 0 i_0 i0:
该步骤没有疑问,正常消除;
P i 0 ( i 1 ) = ∑ i 0 P ( i 0 ) ⋅ P ( i 1 ∣ i 0 ) P ( i 4 ) = ∑ i 1 , i 2 , i 3 P ( i 2 ∣ i 1 ) ⋅ P ( i 3 ∣ i 1 , i 2 ) ⋅ P ( i 4 ∣ i 3 ) ⋅ P i 0 ( i 1 ) \mathcal P_{i_0}(i_1) = \sum_{i_0} \mathcal P(i_0) \cdot \mathcal P(i_1 \mid i_0) \\ \mathcal P(i_4) = \sum_{i_1,i_2,i_3} \mathcal P(i_2 \mid i_1) \cdot \mathcal P(i_3\mid i_1,i_2) \cdot \mathcal P(i_4 \mid i_3) \cdot \mathcal P_{i_0}(i_1) Pi0(i1)=i0∑P(i0)⋅P(i1∣i0)P(i4)=i1,i2,i3∑P(i2∣i1)⋅P(i3∣i1,i2)⋅P(i4∣i3)⋅Pi0(i1) -
第二步:消去变量 i 1 i_1 i1:
仔细观察该部分:
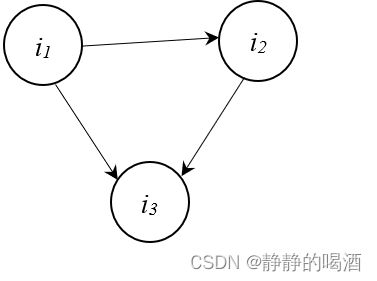
- 从 i 1 i_1 i1的角度观察, i 1 i_1 i1和 i 2 . i 3 i_2.i_3 i2.i3之间属于同父结构。即:
P ( i 2 , i 3 ∣ i 1 ) = P ( i 2 ∣ i 1 ) ⋅ P ( i 3 ∣ i 1 ) \mathcal P(i_2,i_3 \mid i_1) = \mathcal P(i_2 \mid i_1) \cdot \mathcal P(i_3 \mid i_1) P(i2,i3∣i1)=P(i2∣i1)⋅P(i3∣i1) - 从 i 3 i_3 i3的角度观察, i 3 i_3 i3和 i 1 , i 2 i_1,i_2 i1,i2之间是 V \mathcal V V型结构。即:
P ( i 3 ∣ i 1 , i 2 ) = P ( i 3 ∣ i 1 ) ⋅ P ( i 3 ∣ i 2 ) \mathcal P(i_3 \mid i_1,i_2) = \mathcal P(i_3 \mid i_1)\cdot \mathcal P(i_3 \mid i_2) P(i3∣i1,i2)=P(i3∣i1)⋅P(i3∣i2) - 从 i 2 i_2 i2的角度观察, i 2 i_2 i2和 i 1 , i 3 i_1,i_3 i1,i3之间是顺序结构。即:
P ( i 1 , i 3 ∣ i 2 ) = P ( i 1 ∣ i 2 ) ⋅ P ( i 3 ∣ i 2 ) \mathcal P(i_1,i_3 \mid i_2) = \mathcal P(i_1 \mid i_2) \cdot \mathcal P(i_3 \mid i_2) P(i1,i3∣i2)=P(i1∣i2)⋅P(i3∣i2)
在消去 i 1 i_1 i1的过程中,与 i 1 i_1 i1相关的项有: P ( i 3 ∣ i 1 , i 2 ) , P ( i 2 ∣ i 1 ) , P i 0 ( i 1 ) \mathcal P(i_3 \mid i_1,i_2),\mathcal P(i_2 \mid i_1),\mathcal P_{i_0}(i_1) P(i3∣i1,i2),P(i2∣i1),Pi0(i1),基于 V \mathcal V V型结构,将 P ( i 3 ∣ i 1 , i 2 ) \mathcal P(i_3 \mid i_1,i_2) P(i3∣i1,i2)展开,并保留含 i 1 i_1 i1的项:
i 3 i_3 i3未知的条件下,i 1 ⊥ i 2 ∣ i 3 → P ( i 3 ∣ i 1 , i 2 ) = P ( i 3 ∣ i 1 ) ⋅ P ( i 3 ∣ i 2 ) i_1 \perp i_2 \mid i_3 \to \mathcal P(i_3 \mid i_1,i_2) = \mathcal P(i_3 \mid i_1) \cdot \mathcal P(i_3 \mid i_2) i1⊥i2∣i3→P(i3∣i1,i2)=P(i3∣i1)⋅P(i3∣i2)。
P ( i 4 ) = ∑ i 2 , i 3 P ( i 3 ∣ i 2 ) ⋅ P ( i 4 ∣ i 3 ) ⋅ ∑ i 1 P ( i 2 ∣ i 1 ) ⋅ P ( i 3 ∣ i 1 ) ⋅ P i 0 ( i 1 ) \mathcal P(i_4) = \sum_{i_2,i_3} \mathcal P(i_3 \mid i_2) \cdot \mathcal P(i_4 \mid i_3) \cdot \sum_{i_1} \mathcal P(i_2 \mid i_1) \cdot \mathcal P(i_3 \mid i_1) \cdot \mathcal P_{i_0}(i_1) P(i4)=i2,i3∑P(i3∣i2)⋅P(i4∣i3)⋅i1∑P(i2∣i1)⋅P(i3∣i1)⋅Pi0(i1)
先观察后半部分的 i 1 i_1 i1积分项,由于同父结构,可以将 i 1 i_1 i1积分项表示为如下形式:
∑ i 1 P ( i 2 , i 3 ∣ i 1 ) ⋅ P i 0 ( i 1 ) = P i 1 ( i 2 , i 3 ) P ( i 4 ) = ∑ i 2 , i 3 P ( i 3 ∣ i 2 ) ⋅ P ( i 4 ∣ i 3 ) ⋅ P i 1 ( i 2 , i 3 ) \sum_{i_1} \mathcal P(i_2,i_3 \mid i_1) \cdot \mathcal P_{i_0}(i_1) = \mathcal P_{i_1}(i_2,i_3) \\ \mathcal P(i_4) = \sum_{i_2,i_3} \mathcal P(i_3 \mid i_2) \cdot \mathcal P(i_4 \mid i_3) \cdot \mathcal P_{i_1}(i_2,i_3) i1∑P(i2,i3∣i1)⋅Pi0(i1)=Pi1(i2,i3)P(i4)=i2,i3∑P(i3∣i2)⋅P(i4∣i3)⋅Pi1(i2,i3)
问题所在:观察前半部分的 i 2 , i 3 i_2,i_3 i2,i3积分项,基于前面的 P i 1 ( i 2 , i 3 ) \mathcal P_{i_1}(i_2,i_3) Pi1(i2,i3),我们更希望凑出 P ( i 4 ∣ i 2 , i 3 ) \mathcal P(i_4 \mid i_2,i_3) P(i4∣i2,i3),从而得到:
P ( i 4 ) = ∑ i 2 , i 3 P ( i 4 ∣ i 2 , i 3 ) ⋅ P i 1 ( i 2 , i 3 ) = P i 2 , i 3 ( i 4 ) \begin{aligned} \mathcal P(i_4) & = \sum_{i_2,i_3} \mathcal P(i_4 \mid i_2,i_3) \cdot \mathcal P_{i_1}(i_2,i_3) \\ & = \mathcal P_{i_2,i_3}(i_4) \end{aligned} P(i4)=i2,i3∑P(i4∣i2,i3)⋅Pi1(i2,i3)=Pi2,i3(i4)
但实际上,并没有办法证明:
P ( i 4 ∣ i 2 , i 3 ) = P ( i 4 ∣ i 3 ) ⋅ P ( i 3 ∣ i 2 ) \mathcal P(i_4 \mid i_2,i_3) = \mathcal P(i_4 \mid i_3) \cdot \mathcal P(i_3 \mid i_2) P(i4∣i2,i3)=P(i4∣i3)⋅P(i3∣i2)
欢迎小伙伴们一起讨论。指出错误,有正确的推导一起分享,非常感谢。 - 从 i 1 i_1 i1的角度观察, i 1 i_1 i1和 i 2 . i 3 i_2.i_3 i2.i3之间属于同父结构。即:
下一节将介绍信念传播(Belief Propagation,BP)。
相关参考:
机器学习-周志华著
机器学习-概率图模型8-推断Inference-Variable Elimination