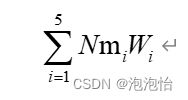机器学习——BP神经网络详细介绍及案例Python代码实现

哒哒！来咯！来喽！

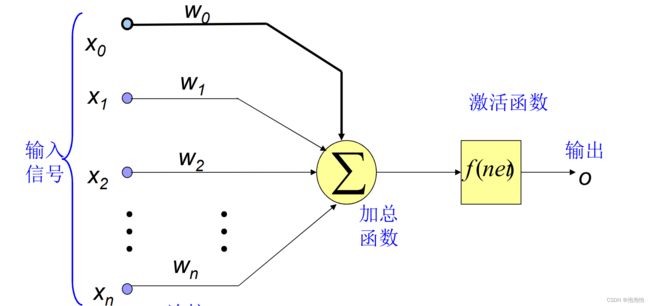
BP（Back Propagation)称误差反向传播，1985年由Rumelhart 和 McCelland提出。神经元函数如图：

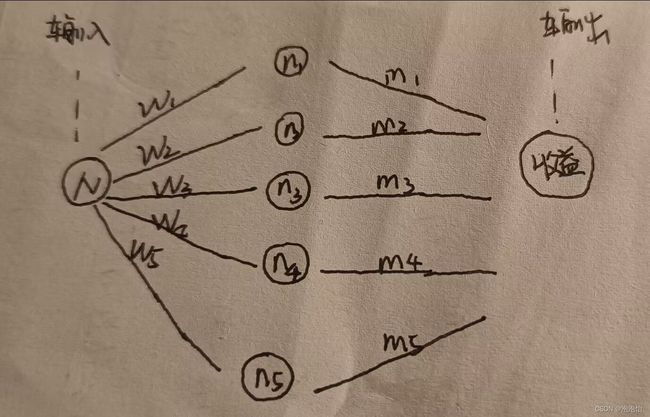
（一）、举个通俗易懂的例子：假如，我说的是假如喔，我拥有N个亿，那肯定不用说了，我的N肯定是极限中lim下的正无穷啦！我要进行投资给五个公司，投给每个公司的权重分别为w1、w2、w3、w4、w5，而每个公司我的收益是不同的分别为：m1、m2、m3、m4、m5，最后我的总收益为：

 

那么问题来了，神经网络可以这么表示（如下图）：

（二）、反向传播

学过Java想必大家都会编写猜数小游戏，你设定一个数，限制猜这个数的次数，比如：我设定数字为66，第一次你猜33，我说小了。对于我的信息反馈就是反向传播  ，你说的信息是正向传播。从这里你是否可以感觉这个反向传播，是不是很像测量值与真实值之间的误差信息。

（三）、激活函数——需要用一个非线性函数，将线性分量用于输入。需要通过将激活函数应用于线性组合来完成。激活函数将输入信号转换为输出信号。应用激活函数后的输出为f(a⋅W1+b))f(a⋅W1+b))，其中f()就是激活函数。

Sigmoid——最常用的激活函数之一，它被定义为 ：

 
　　Sigmoid变换呈现出值域为[0,1]的S型生长曲线。如果你需要观察在输入变化极小的情况下，输出值的变化，此时Sigmoid函数优于阶跃函数。

（四）BP神经网络

 从上图我们看到了，神经元函数的构造：我们发现了激活函数，激活函数就是在隐藏层中发挥着作用，当我们利用神经网络做回归的时候最后一列的隐层不含有激活函数，激活函数的作用就是非线性组合，也不知道大家会不会理解，那就再画个简单的图（这个里面没有添加偏置项b在架构网络的时候大家可以设定）：

所以在我们进行建模竞赛的时候 ，对于多变量的关系可以采取拟合或者线性回归。

那么BP神经网络的反向在哪里呢？ 

在我们进行权值计算的时候，我们得到的结果还可以和真实值进行对比也就是损失函数（loss）。

损失函数（loss）——建立一个网络时，为了将结果预测得尽可能靠近实际值。我们使用损失函数来衡量网络的准确，而损失函数会在发生错误时尝试惩罚网络。运行网络的目标是提高预测精度并减少误差，从而最大限度地降低成本。最优化的输出是那些成本或损失函数值最小的输出。

正向传播就是：我们通过输入让信息从输入层进入神经网络。

不知道会不会有人和我有一样的问题：它求不出来表达式，那可以干嘛呢？可以预测呀，很重要的！

（五）、房价预测实例

1.数据集：

 2.代码（和前面博文的步骤一样，只是不同在函数的调用）

from sklearn.datasets import load_boston
import numpy as np
import pandas as pd
data=pd.read_csv('./data_picture/chapter1/boston_house_prices.csv')
data.head()
from sklearn.model_selection import train_test_split
X=data.drop('MEDV',axis=1)   
y=data['MEDV']               
X=X.values                   
y=y.values                   
X_train,X_test,y_train,y_test=train_test_split(X,y,random_state=33,test_size=0.25)
from sklearn.preprocessing import StandardScaler
ss_X=StandardScaler()
scaler_X=ss_X.fit(X_train)
X_train=scaler_X.transform(X_train)
X_test=scaler_X.transform(X_test)
from sklearn.neural_network import MLPRegressor
model = MLPRegressor(solver='lbfgs', hidden_layer_sizes=(15,15), random_state=1)
model.fit(X_train, y_train)
from sklearn.metrics import r2_score,mean_squared_error,mean_absolute_error
print('训练集回归评估指标：')
model_score1=model.score(X_train,y_train)  
print('The accuracy of train data is',model_score1)  
print('测试集回归评估指标：')
model_score2=model.score(X_test,y_test) 
print('The accuracy of test data is',model_score2)  
y_test_predict=model.predict(X_test)
mse=mean_squared_error(y_test,y_test_predict)   
print('The value of mean_squared_error:',mse)
mae=mean_absolute_error(y_test,y_test_predict) 
print('The value of mean_absolute_error:',mae)

结果：

3.新的数据进行预测：

new_data=np.array([[0.22489,12.5,7.87,0,0.524,6.377,94.3,6.3467, 5.,311,15.2,392.52,20.45],
                   [0.3489,11.5,7.7,0,0.526,6.477,94.3,16.3467, 5.,313,15.2,392.55,20.45]])
X_new=scaler_X.transform(new_data) #标准化
y_new=model.predict(X_new)        #预测
print(y_new)

 结果：

 房价预测范围。