【论文阅读笔记 + 代码解读】（2018 AAAI）ST-GCN
写在前面
ST-GCN 是skeleton based action recognition 的开山鼻祖。MMLab 出品，必是精品！
开山鼻祖级别的论文必有很多理论 + 数学公式，再加上本人（菜鸡）既不是数学专业又不是计软本科出身的，所以第一次看这篇论文的时候很痛苦。。。
所以本来应该很早就要写这篇博客的，被我拖啊拖。。。拖到了 2s-AGCN 的解读博客我都写完好久了，ST-GCN 的还是没出来。。。解读 2s-AGCN 代码_小吴同学真棒的博客-CSDN博客_2s-agcn代码论文：https://openaccess.thecvf.com/content_CVPR_2019/papers/Shi_Two-Stream_Adaptive_Graph_Convolutional_Networks_for_Skeleton-Based_Action_Recognition_CVPR_2019_paper.pdf论文代码：https://github.com/lshiwjx/2s-AGCNA（Graph）的定义https://git...https://blog.csdn.net/qq_36627158/article/details/115299754
于是本周痛下决心，必啃下数学公式，写完这篇论文的解读！
注意，这篇解读博客的面向对象是像初学者或者想我这样的小菜鸡，会写的比较细。
我加了一些自己的解读，如果大佬们发现错误的话，轻批好吗？
code：https://github.com/yysijie/st-gcn
Spatial temporal graph convolutional networks for skeleton-based action recognition
（2018 AAAI）
Sijie Yan, Yuanjun Xiong, Dahua Lin
Notes
Contributions
1) We propose ST-GCN, a generic graph-based formulation for modeling dynamic skeletons, which is the first that applies graph-based neural networks for this task.
2) We propose several principles in designing convolution kernels in ST-GCN to meet the specific demands in skeleton modeling.
3) On two large scale datasets for skeleton-based action recognition, the proposed model achieves superior performance as compared to previous methods using hand-crafted parts or traversal rules, with considerably less effort in manual design.
Method
Pipeline
Given the sequences of body joints in the form of 2D or 3D coordinates, we construct a spatial temporal graph with the joints as graph nodes and natural connectivities in both human body structures and time as graph edges. The input to the ST-GCN is therefore the joint coordinate vectors on the graph nodes. Multiple layers of spatial-temporal graph convolution operations will be applied on the input data and generating higher-level feature maps on the graph. It will then be classified by the standard SoftMax classifier to the corresponding action category. The whole model is trained in an end-to-end manner with backpropagation.
Skeleton Graph Construction
We construct an undirected spatial temporal graph G = (V, E) on a skeleton sequence with N joints and T frames featuring both intra-body and inter-frame connection to represent the skeleton sequences.
In this graph, the node set V = {vti|t = 1, . . . , T, i = 1, . . . ,N} includes the all the joints in a skeleton sequence. As ST-GCN’s input, the feature vector on a node F(vti) consists of coordinate vectors, as well as estimation confidence, of the i-th joint on frame t. We construct the spatial temporal graph on the skeleton sequences in two steps. First, the joints within one frame are connected with edges according to the connectivity of human body structure, which is illustrated in Fig. 1. Then each joint will be connected to the same joint in the consecutive frame. On the Kinetics dataset, we use the 2D pose estimation results from the OpenPose (Cao et al. 2017b) toolbox which outputs 18 joints, while on the NTU- RGB+D dataset (Shahroudy et al. 2016) we use 3D joint tracking results as input, which produces 25 joints.
Formally, the edge set E is composed of two subsets, the first subset depicts the intra-skeleton connection at each frame, denoted as ES = {vtivtj|(i, j) ∈ H}, where H is the set of naturally connected human body joints. The second subset contains the inter-frame edges, which connect the same joints in consecutive frames as EF = {vtiv(t+1)i}. Therefore all edges in EF for one particular joint i will represent its trajectory over time.
skeleton data 长什么样可以之前 2s-AGCN 这篇解读博客：
解读 2s-AGCN 代码_小吴同学真棒的博客-CSDN博客_2s-agcn代码论文：https://openaccess.thecvf.com/content_CVPR_2019/papers/Shi_Two-Stream_Adaptive_Graph_Convolutional_Networks_for_Skeleton-Based_Action_Recognition_CVPR_2019_paper.pdf论文代码：https://github.com/lshiwjx/2s-AGCNA（Graph）的定义https://git...https://blog.csdn.net/qq_36627158/article/details/115299754
ST-GCN 中 构造图 的代码如下：
https://github.com/yysijie/st-gcn/blob/master/net/utils/graph.py#L41https://github.com/yysijie/st-gcn/blob/master/net/utils/graph.py#L41
def get_edge(self, layout):
if layout == 'openpose':
self.num_node = 18
self_link = [(i, i) for i in range(self.num_node)]
neighbor_link = [(4, 3), (3, 2), (7, 6), (6, 5), (13, 12), (12, 11),
(10, 9), (9, 8), (11, 5), (8, 2), (5, 1), (2, 1),
(0, 1), (15, 0), (14, 0), (17, 15), (16, 14)]
self.edge = self_link + neighbor_link
self.center = 1
elif layout == 'ntu-rgb+d':
self.num_node = 25
self_link = [(i, i) for i in range(self.num_node)]
neighbor_1base = [(1, 2), (2, 21), (3, 21), (4, 3), (5, 21),
(6, 5), (7, 6), (8, 7), (9, 21), (10, 9),
(11, 10), (12, 11), (13, 1), (14, 13), (15, 14),
(16, 15), (17, 1), (18, 17), (19, 18), (20, 19),
(22, 23), (23, 8), (24, 25), (25, 12)]
neighbor_link = [(i - 1, j - 1) for (i, j) in neighbor_1base]
self.edge = self_link + neighbor_link
self.center = 21 - 1
elif layout == 'ntu_edge':
self.num_node = 24
self_link = [(i, i) for i in range(self.num_node)]
neighbor_1base = [(1, 2), (3, 2), (4, 3), (5, 2), (6, 5), (7, 6),
(8, 7), (9, 2), (10, 9), (11, 10), (12, 11),
(13, 1), (14, 13), (15, 14), (16, 15), (17, 1),
(18, 17), (19, 18), (20, 19), (21, 22), (22, 8),
(23, 24), (24, 12)]
neighbor_link = [(i - 1, j - 1) for (i, j) in neighbor_1base]
self.edge = self_link + neighbor_link
self.center = 2
# elif layout=='customer settings'
# pass
else:
raise ValueError("Do Not Exist This Layout.")Spatial Graph Convolutional Neural Network
Recall the definition of convolution operation on the 2D natural images or feature maps, which can be both treated as 2D grids. The output feature map of a convolution operation is again a 2D grid. With stride 1 and appropriate padding, the output feature maps can have the same size as the input feature maps. We will assume this condition in the following discussion. Given a convolution operator with the kernel size of K×K, and an input feature map fin with the number of channels c. The output value for a single channel at the spatial location x can be written as
The convolution operation on graphs is then defined by extending the formulation above to the cases where the input features map resides on a spatial graph Vt. That is, the feature map ftin : Vt → Rc has a vector on each node of the graph. The next step of the extension is to redefine the sampling function p and the weight function w.
Sampling function
On graphs, we can similarly define the sampling function on the neighbor set 
of a node 
. Here 
denotes the minimum length of any path from 
to 
. Thus the sampling function 
can be written as
In this work we use 
for all cases, that is, the 1 neighbor set of joint nodes. The higher number of 
is left for future works.
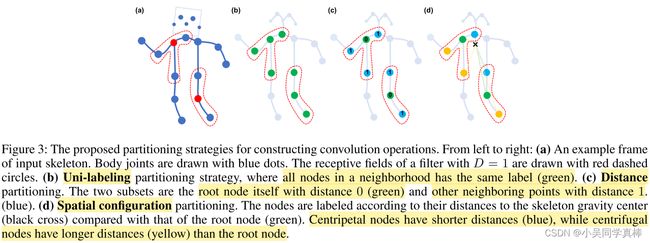
本文又将 neighbor set + itself 按照三种不同的划分方法，将其设置为不同的 subset：
Partition Strategies. In this work we explore several partition strategies to implement the label map l. For simplicity, we only discuss the cases in a single frame.
1. Uni-labeling. In this strategy, feature vectors on every neighboring node will have a inner product with the same weight vector. Using this strategy is equivalent to computing the inner product between the weight vector and the average feature vector of all neighboring nodes. Formally, we have K=1 and 
.
2. Distance partitioning. Another natural partitioning strategy is to partition the neighbor set according to the nodes' distance 
to the root node 
. In this work, because we set D=1, the neighbor set will then be separated into two subsets, where d=0 refers to the root node itself and remaining neighbor nodes are in the d=1 subset. Thus we will have two different weight vectors and they are capable of modeling local differential properties such as the relative translation between joints. Formally, we have K=2 and 
.
3. Spatial configuration partitioning. We divide the neighbor set into three subsets:
1) the root node itself;
2) centripetal group: the neighboring nodes that are closer to the gravity center of the skeleton than the root node;
3) otherwise the centrifugal group.
Here the average coordinate of all joints in the skeleton at a frame is treated as its gravity center. This strategy is inspired by the fact that motions of body parts can be broadly categorized as concentric and eccentric motions. Formally, we have
where 
is the average distance from gravity center to joint i
over all frames in the training set.
ST-GCN 中 三种划分方法（定义邻接矩阵） 部分的代码如下：
https://github.com/yysijie/st-gcn/blob/master/net/utils/graph.py#L78
def get_adjacency(self, strategy):
valid_hop = range(0, self.max_hop + 1, self.dilation)
adjacency = np.zeros((self.num_node, self.num_node))
for hop in valid_hop:
adjacency[self.hop_dis == hop] = 1
normalize_adjacency = normalize_digraph(adjacency)
if strategy == 'uniform':
A = np.zeros((1, self.num_node, self.num_node))
A[0] = normalize_adjacency
self.A = A
elif strategy == 'distance':
A = np.zeros((len(valid_hop), self.num_node, self.num_node))
for i, hop in enumerate(valid_hop):
A[i][self.hop_dis == hop] = normalize_adjacency[self.hop_dis ==
hop]
self.A = A
elif strategy == 'spatial':
A = []
for hop in valid_hop:
a_root = np.zeros((self.num_node, self.num_node))
a_close = np.zeros((self.num_node, self.num_node))
a_further = np.zeros((self.num_node, self.num_node))
for i in range(self.num_node):
for j in range(self.num_node):
if self.hop_dis[j, i] == hop:
if self.hop_dis[j, self.center] == self.hop_dis[
i, self.center]:
a_root[j, i] = normalize_adjacency[j, i]
elif self.hop_dis[j, self.
center] > self.hop_dis[i, self.
center]:
a_close[j, i] = normalize_adjacency[j, i]
else:
a_further[j, i] = normalize_adjacency[j, i]
if hop == 0:
A.append(a_root)
else:
A.append(a_root + a_close)
A.append(a_further)
A = np.stack(A)
self.A = A
else:
raise ValueError("Do Not Exist This Strategy")Weight Function
On images, the weight function can then be implemented by indexing a tensor of (c,K,K) dimensions according to the spatial order. On graph, the order is defined by a graph labeling process in the neighbor graph around the root node. Instead of giving every neigh-bor node a unique labeling, we simplify the process by partitioning the neighbor set 
of a joint node 
into a fixed number of K subsets, where each subset has a numeric label.
Thus we can have a mapping 
which maps a node in the neighborhood to its subset label. The weight function 
can be implemented by indexing a tensor of (c,K) dimension or
假设二维图像的卷积核大小为 3*3，则
二维图像的卷积核shape为 (c, 3, 3)，ouput 里的 1 个 pixel 的感受野为 3*3=9 个 pixel。感受野里的每一个 pixel 与 一个 weight vector (c, 1, 1) 进行点积。所以，感受野里 3*3=9 个像素分别对应着 9 个不同的卷积核里的值。
而这篇论文是将现在某个节点的感受野（自己+邻接节点）分为 K 个subset，每个 subset 里的所有节点都 share 一个 weight vector (c, 1)，所以，卷积核的shape为 (c, k)。
ST-GCN 中 实现 weight function 部分的代码如下：
https://github.com/yysijie/st-gcn/blob/master/net/utils/tgcn.py#L6
class ConvTemporalGraphical(nn.Module):
r"""The basic module for applying a graph convolution.
Args:
in_channels (int): Number of channels in the input sequence data
out_channels (int): Number of channels produced by the convolution
kernel_size (int): Size of the graph convolving kernel
t_kernel_size (int): Size of the temporal convolving kernel
t_stride (int, optional): Stride of the temporal convolution. Default: 1
t_padding (int, optional): Temporal zero-padding added to both sides of
the input. Default: 0
t_dilation (int, optional): Spacing between temporal kernel elements.
Default: 1
bias (bool, optional): If ``True``, adds a learnable bias to the output.
Default: ``True``
Shape:
- Input[0]: Input graph sequence in :math:`(N, in_channels, T_{in}, V)` format
- Input[1]: Input graph adjacency matrix in :math:`(K, V, V)` format
- Output[0]: Outpu graph sequence in :math:`(N, out_channels, T_{out}, V)` format
- Output[1]: Graph adjacency matrix for output data in :math:`(K, V, V)` format
where
:math:`N` is a batch size,
:math:`K` is the spatial kernel size, as :math:`K == kernel_size[1]`,
:math:`T_{in}/T_{out}` is a length of input/output sequence,
:math:`V` is the number of graph nodes.
"""
def __init__(self,
in_channels,
out_channels,
kernel_size,
t_kernel_size=1,
t_stride=1,
t_padding=0,
t_dilation=1,
bias=True):
super().__init__()
self.kernel_size = kernel_size
self.conv = nn.Conv2d(
in_channels,
out_channels * kernel_size,
kernel_size=(t_kernel_size, 1),
padding=(t_padding, 0),
stride=(t_stride, 1),
dilation=(t_dilation, 1),
bias=bias)
def forward(self, x, A):
assert A.size(0) == self.kernel_size
x = self.conv(x)
n, kc, t, v = x.size()
x = x.view(n, self.kernel_size, kc//self.kernel_size, t, v)
x = torch.einsum('nkctv,kvw->nctw', (x, A))
return x.contiguous(), ASpatial Graph Convolution
With the refined sampling function and weight function, we now rewrite Eq. 1 in terms of graph convolution as
where the normalizing term 
equals the cardinality of the corresponding subset. This term is added to balance the contributions of different subsets to the output.
Spatial Temporal Modeling
Recall that in the construction of the graph, the temporal aspect of the graph is constructed by connecting the same joints across consecutive frames. This enable us to define a very simple strategy to extend the spatial graph CNN to the spatial temporal domain. That is, we extend the concept of neighborhood to also include temporally connected joints as
The parameter Γ controls the temporal range to be included in the neighbor graph and can thus be called the temporal kernel size. To complete the convolution operation on the spatial temporal graph, we also need the sampling function, which is the same as the spatial only case, and the weight function, or in particular, the labeling map 
. Because the temporal axis is well-ordered, we directly modify the label map 
for a spatial temporal neighborhood rooted at 
to be
where 
is the label map for the single frame case at 
. In this way, we have a well-defined convolution operation on the constructed spatial temporal graphs.
时间维度上的卷积就是普通的卷积。
这里的 l_ST 是 sptial + temporal 的 label map。
假设当前 t = 20，Γ = 9。那么，temporal 感受野为：t=【16~24】
那么 t = 16 里 3 个 subset 的 label 分别为：1 + (16-20+4)*3 = 1、 2 + (16-20+4)*3 = 2、 3 + (16-20+4)*3 = 3
那么 t = 17 里3个 subset 的 label 分别为为 1 + (17-20+4)*3 = 4、 2 + (17-20+4)*3 = 5、 3 + (17-20+4)*3 = 6
以此类推。
Learnable edge importance weighting
Although joints move in groups when people are performing actions, one joint could appear in multiple body parts. These appearances, however, should have different importance in modeling the dynamics of these parts. In this sense, we add a learnable mask M (shape: [N, N]) on every layer of spatial temporal graph convolution. The mask will scale the contribution of a node’s feature to its neighboring nodes based on the learned importance weight of each spatial graph edge in ES.
W 和 M 区别：
W 的维度为（K，V），其中 K 是subset 的个数，V 是节点数
M的维度是（V，V）
Implementing ST-GCN
The intra-body connections of joints within a single frame are represented by an adjacency matrix A and an identity matrix I representing self-connections.
In the single frame case, ST-GCN with the first partitioning strategy can be implemented with the following formula (Kipf and Welling 2017)
where 
. Here the weight vectors of multiple output channels are stacked to form the weight matrix W. In practice, under the spatial temporal cases, we can represent the input feature map as a tensor of (C,V,T) dimensions. The graph convolution is implemented by performing a 1×Γ standard 2D convolution and multiplies the resulting tensor with the normalized adjacency matrix 
on the second dimension.
For partitioning strategies with multiple subsets, i.e., distance partitioning and spatial configuration partitioning, we again utilize this implementation. But note now the adjacency matrix is dismantled into several matrixes 
where 
For example in the distance partitioning strategy, 
and 
.
The above Equation is transformed into
where similarly 
. Here we set α=0.001 to avoid empty rows in 
.
It is straightforward to implement the learnable edge importance weighting. For each adjacency matrix, we accompany it with a learnable weight matrix M. And we substitute the matrix A+I in Eq. 9 and Aj in Eq. 10 with (A+I)⊗M and Aj⊗M, respectively. Here ⊗ denotes element-wise product between two matrixes. The mask M is initialized as an all-one matrix.
Results
Baseline TCN. We use a baseline network architecture (Kim and Reiter 2017) where all spatial temporal convolutions are replaced by only temporal convolution. That is, we concatenate all input joint locations to form the input features at each frame t. The temporal convolution will then operate on this input and convolves over time.
Local Convolution. we evaluate an intermediate model between the baseline model and ST-GCN. In this model we use the sparse joint graph as ST-GCN, but use convolution filters with unshared weights.
相当于用图卷积，但不使用共享卷积核。
如果shared，说明每个节点的卷积核是共享的；不使用共享卷积核意思就是每个节点自己学习一个卷积核。
Distance Partitioning *. In this setting we bind the weights of the two subsets in distance partitioning to be different only by a scaling factor −1, or w0 = −w1.
原来的 distance partitioning是学习 2 个 weight vector。
这个 distance partitioning* 是学习 1 个 weight vector，另一个 weight vector 直接取反
ST-GCN+Imp. We experiment with adding the learnable edge importance weighting on the ST-GCN model with spatial configuration partitioning.
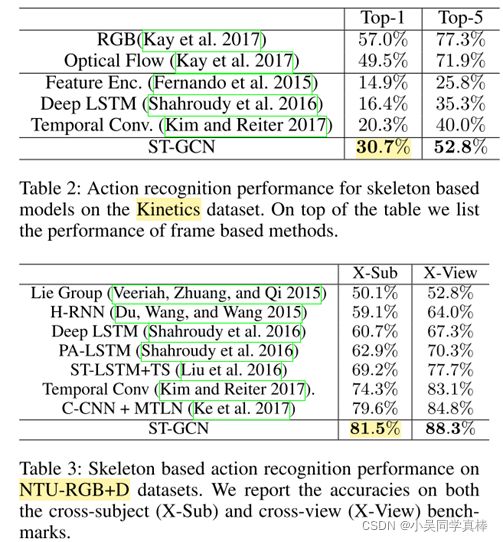
We also notice that on Kinetics the accuracies of skeleton based methods are inferior to video frame based models (Kay et al. 2017). We argue that this is due to a lot of action classes in Kinetics requires recognizing the objects and scenes that the actors are interacting with. To verify this, we select a subset of 30 classes strongly related with body motions, named as “Kinetics-Motion” and list the mean class accuracies of skeleton and frame based models (Kay et al. 2017) on this subset in Table 4.
We also explore using ST-GCN to capture motion information in two-stream style action recognition. As shown as in Table. 5, our skeleton based model ST-GCN can also provide complementary information to RGB and optical flow models. We train the standard TSN (Wang et al. 2016) models from scratches on Kinetics with RGB and optical flow models.