时序预测 | MATLAB实现GMDH自组织网络模型时间序列预测(COVID预测-病例预测)

时序预测 | MATLAB实现GMDH自组织网络模型时间序列预测(COVID预测-病例预测)

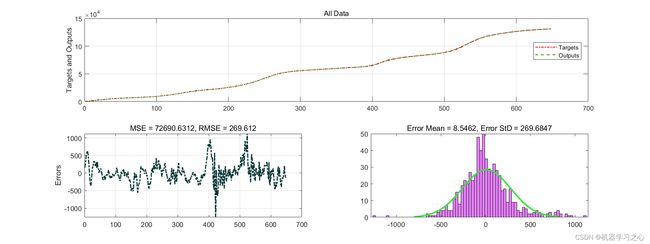
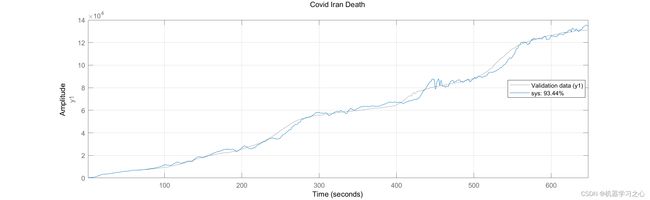
效果一览

基本介绍

GMDH自组织网络模型是自组织数据挖掘中的一种模型方法，是基于计算机科学和神经网络的迅速发展而产生和发展的.在信息爆炸和信息不完全的求解条件下，自组织方法能够有效避免个人主观因素的干扰.,是前苏联乌克兰科学院的 1968年运用多层神经网络原理和品种改良假说提出的一种复杂非线性系统的启发式自组织建模方法，以 K-G多项式为基础通过不断筛选组合建立非线性系统的模型，对高阶非线性系统的辨识很有效。GMDH神 经 网 络 是 前 馈 神 经 网络中一种用于预测的实用神经网络，其特点是网络结构不固定，在训练过程中不断变化。GMDH神经网络具有以下特点：
（１）建 模 过 程 自 组 织 控 制，不 需 任 何 初 始假设；
（２）最优复杂性及高精度预测；
（３）能够自组织多层神经网络每层的最佳结构，即能够自动保留有用变量和删除多余变量；
（４）能够自动选择最佳网络层数和每层的神经元数目。GMDH 算法由系统各输入单元交叉组合产生一系列的活动神经元，其中每一神经元都具有选择最优传递函数的功能，再从已产生的一代神经元中选择若干与目标变量最为接近的神经元，被选出神经元强强结合再次产生新的神经元，重复这样的优势遗传、竞争生存和进化的过程，直至具有最佳复杂性的模型被选出。

模型构建

程序设计

• 完整程序和数据下载：GMDH自组织网络模型时间序列预测
• 运行主程序MainGMDHTS.m即可。

%--------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
%% GMDH时间序列预测
%% 环境准备
clc
clear;
close all;
%--------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
%% 可视化
% figure;
% PlotResults(TrainTargets, TrainOutputs, 'Train Data');
% figure;
% PlotResults(TestTargets, TestOutputs, 'Test Data');
figure;
set(gcf, 'Position',  [50, 100, 1200, 450])
[MSE RMSE ErrorMean ErrorStd Errors]=PlotResults(Targets, Outputs, 'All Data');
figure;
plotregression(TrainTargets, TrainOutputs, 'Train Data', ...
               TestTargets, TestOutputs, 'TestData', ...
               Targets, Outputs, 'GMDH All Data');
%--------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
% Forecast Plot
fore=180;
sizee=size(x);
sizee=sizee(1,2);
forecasted=Outputs(1,end-fore:end);
forecasted=forecasted+x(end)/2.5;
ylbl=sizee+fore;
t = linspace(sizee,ylbl,length(forecasted));
%--------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
% Compare the simulated output with measured data to ensure it is a good fit.
nstep=32;
sys = nlarx(Outputs',64);
figure;
set(gcf, 'Position',  [50, 200, 1300, 400])
compare(Outputs',sys,nstep);title('Covid Iran Death');
grid on;
%--------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
figure;
regres=compare(Outputs',sys,nstep);title('Covid Iran Death');
b1 = regres\Outputs';
yCalc1 = b1*regres;
scatter(regres,Outputs','MarkerEdgeColor',[0 .5 .5],...
              'MarkerFaceColor',[0 .8 .8],...
              'LineWidth',1);
hold on
plot(regres,yCalc1,':',...
    'LineWidth',2,...
    'MarkerSize',5,...
    'Color',[0.6350 0.0780 0.1840]);
title(['Regression :   ' num2str(b1) ])
grid on
%--------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
%
figure;
set(gcf, 'Position',  [20, 20, 1000, 250])
plot(x,'--',...
    'LineWidth',1,...
    'MarkerSize',5,...
    'Color',[0,0,0.7]);
hold on;
plot(t,forecasted,'-.',...
    'LineWidth',2,...
    'MarkerSize',10,...
    'Color',[0.9,0.5,0]);
title('COVID Deaths - Orange is Forcasted')
xlabel('Days - From Jan 2020 Till Dec 2021','FontSize',12,...
       'FontWeight','bold','Color','b');
ylabel('Number of People','FontSize',12,...
       'FontWeight','bold','Color','b');
   datetick('x','mmm');
legend({'Measured','GMDH Forecasted'});
%--------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
%% 指标分析
% Explained Variance (EV)
va=var(Outputs-Targets);vc=var(Targets);
vd=abs(va/vc);vb = vd / 10^floor(log10(vd));
EV=vb*0.1
%--------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
% MSE
MSE 
% RMSE
RMSE
% Mean Error
ErrorMean
% STD Error
ErrorStd 
% Mean Absolute Error (MAE)
MAE = mae(Targets,Outputs)
% Root Mean Squared Log Error (RMSLE) 
RMSLE = sum((log(Targets)-log(Outputs)).^2)*0.1
%--------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
function [X, Y] = CreateTimeSeriesData(x, Delays)

    T = size(x,2);
    
    MaxDelay = max(Delays);
    
    Range = MaxDelay+1:T;
    
    X= [];
    for d = Delays
        X=[X; x(:,Range-d)];
    end
    
    Y = x(:,Range);

end
%--------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
function p = FitPolynomial(x1, Y1, x2, Y2, vars)
    
    X1 = CreateRegressorsMatrix(x1);
    c = Y1*pinv(X1);
    
    Y1hat = c*X1;
    e1 = Y1- Y1hat;
    MSE1 = mean(e1.^2);
    RMSE1 = sqrt(MSE1);
    
    f = @(x) c*CreateRegressorsMatrix(x);
    
    Y2hat = f(x2);
    e2 = Y2- Y2hat;
    MSE2 = mean(e2.^2);
    RMSE2 = sqrt(MSE2);
    
    p.vars = vars;
    p.c = c;
    p.f = f;
    p.Y1hat = Y1hat;
    p.MSE1 = MSE1;
    p.RMSE1 = RMSE1;
    p.Y2hat = Y2hat;
    p.MSE2 = MSE2;
    p.RMSE2 = RMSE2;

end
%--------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
function X = CreateRegressorsMatrix(x)

    X = [ones(1,size(x,2))
         x(1,:)
         x(2,:)
         x(1,:).^2
         x(2,:).^2
         x(1,:).*x(2,:)];

end
%--------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

学习总结

GMDH算法通过遗传、变异和选择，从一个简单的初始模型生成很多具有不断增长复杂度的候选模型，直至模型在观测样本数据上产生过拟合，即最优复杂度为止。

参考资料

[1] https://download.csdn.net/download/kjm13182345320/86818342?spm=1001.2014.3001.5501
[2] https://blog.csdn.net/kjm13182345320/article/details/127484826?spm=1001.2014.3001.5501
[3] https://download.csdn.net/download/kjm13182345320/86811416?spm=1001.2014.3001.5501