训练模型的技巧方法
深度学习的秘诀(Recipe)
在深度学习上其实并没有很容易overfitting
-
因此,深度学习学习好网络后,我们应该先检查Training Data上的正确率,因为模型并不一定能够训练起来。
如果NO,这个时候算是underfitting(欠拟合),你需要先想办法,将训练集训练起来
-
然后才去检查Testing Set上
如果这个时候是NO,那么这个时候就是overfitting过拟合
——不同的方法用于不同的问题
训练集表现不好
新的激活函数
-
神经网络架构地不好
因此有一个方法是——New activation function
——Deep 不等于 imply better
如上图所示,你会发现当隐藏层逐渐增多的时候,这个Train的结果就坏掉了
——Why?
梯度消失问题
当你把network叠得很深的时候:
- 靠近input那几层的微分是很小的,因此它参数update起来是很慢的
- 靠近output那几层的微分是很大的,因此它参数update起来是很快的
因此当你前面那几层神经网络的参数还在random的时候,后面那几层神经网络就已经根据那几层random的参数,逐渐converge(收敛)起来了
——这个时候你就会发现Loss的下降变得很慢;
——因为靠近output那几层神经网络,基本上就是based on random的数据进行收敛的(即可能到达了某个局部最优点),所以你的模型最后的表现不太好。
为什么有这样的情况发生呢?
本质上梯度的影响就是,我们改变一个小小的参数,他最后对cost function的影响有多大?
我们通过改变w的权值,都加上 Δ w \Delta w Δw,最后的output变化是很小的
——说明,这个参数的影响是会递减的
——你就会发现,每经过一次Sigmoid function,这个影响就会衰减一次;因此你的神经网络越深,经过的Sigmoid function的次数越多,衰减越厉害,对最后Cost的影响就很小
怎么解决这件事呢?
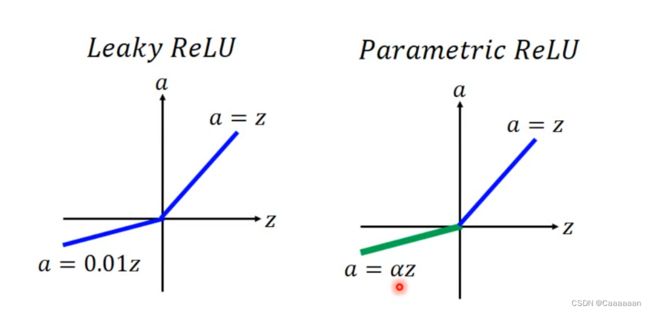
ReLU
早期的发明RBM是去做pre-train;就是我们先把第一层Train好,再把第二层Train好…
然后有人提出一个方法,修改一下这个Sigmoid Function,可能就有用的
——现在常用的激活函数
——Rectified Linear Unit(ReLU)
——Reason
-
计算快速
相比于Sigmoid Function,这个函数的计算快得多,Sigmoid Function里面还有指数
-
生物上的原因
-
具有无限多个不同偏差的Sigmoid 函数
ReLU等同于是无穷多个sigmoid function叠加的结果
-
解决梯度消失的问题
在以全部都是ReLU的激活函数形成的神经网络中,经过ReLU的output要么是0,要么就是input
——output是0的那些神经元根本就不会影响到最后的结果,甚至可以把它从network里拿掉
——如果output=input,这个时候是Linear的
于是你得到的最后的network,就是一个很长的Linear network
如果你的network是Linear的话,就不会存在某个梯度变小的事
——但是network整体上来看还是non-linear的
ReLU变型
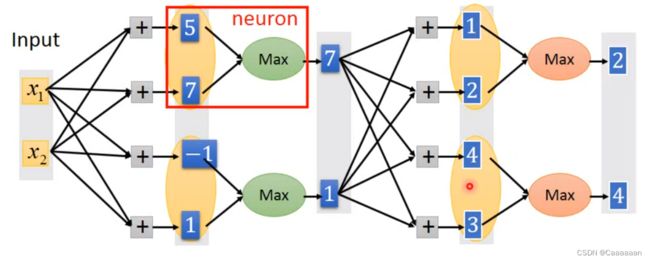
Maxout
ReLU是Maxout的特殊形式
- Maxout network能够让机器自动去学习激活函数
将一些output作为一个群Group起来,然后去群里的较大值
怎么group,多少个放到一个group都是可以由你自己决定的
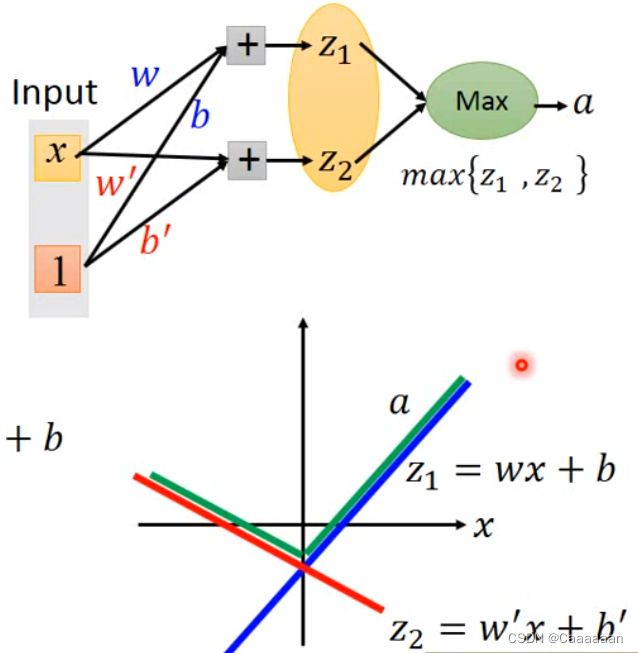
ReLU本质上就是max(0,output1)
——但是Maxout是可以做出更多的激活函数
- 因此,激活函数在maxout network里面,可以是任何分段的线性凸函数
- 有多少段,取决于有多少元素在一个group里面
How TRAIN
——那现在的问题是,这个maxout network怎么train?
——我们取的是max,应该怎么做微分?
max的运算,其实本质上就是linear的运算,其他没有选到的,可以去掉,对网络运算没有任何影响
——没有选到的权重怎么train呢?
-
这个在实作上并不是一个问题
-
因为在实作上,每一笔输入的input不一样,你的网络的z值和max选择的值是不一样的,也就是每一笔不同的输入,这个network的结构都是不一样的
-
但是我们有很多笔数据,network的结构也在不断地变换
-
因此,实际上每一个权重都可以被训练到
自适应学习率
在梯度下降法的文章中有提及到
——例如Adagrad
梯度下降法_Caaaaaan的博客-CSDN博客_二元函数梯度下降法
——但是,深度学习中,出现的问题,可能是比Adagrad能够解决的问题更复杂的问题
——你可以需要更加dynamic(动态)的调整
RMSProp
ω 1 ← ω 0 − η σ 0 g 0 , σ 0 = g 0 ω 2 ← ω 1 − η σ 1 g 1 , σ 1 = α ( σ 0 ) 2 + ( 1 − α ) ( g 1 ) 2 上式的 α 是可调的超参数 ω 3 ← ω 2 − η σ 2 g 2 , σ 2 = α ( σ 1 ) 2 + ( 1 − α ) ( g 2 ) 2 . . . ω t + 1 ← ω t − η σ t g t , σ t = α ( σ t − 1 ) 2 + ( 1 − α ) ( g t ) 2 \omega^1\leftarrow\omega^0-\frac{\eta}{\sigma^0}g^0,\sigma^0=g^0\\ \omega^2\leftarrow\omega^1-\frac{\eta}{\sigma^1}g^1,\sigma^1=\sqrt{\alpha(\sigma^0)^2+(1-\alpha)(g^1)^2}\\ 上式的\alpha是可调的超参数\\ \omega^3\leftarrow\omega^2-\frac{\eta}{\sigma^2}g^2,\sigma^2=\sqrt{\alpha(\sigma^1)^2+(1-\alpha)(g^2)^2}\\ ...\\ \omega^{t+1}\leftarrow\omega^t-\frac{\eta}{\sigma^t}g^t,\sigma^t=\sqrt{\alpha(\sigma^{t-1})^2+(1-\alpha)(g^t)^2} ω1←ω0−σ0ηg0,σ0=g0ω2←ω1−σ1ηg1,σ1=α(σ0)2+(1−α)(g1)2上式的α是可调的超参数ω3←ω2−σ2ηg2,σ2=α(σ1)2+(1−α)(g2)2...ωt+1←ωt−σtηgt,σt=α(σt−1)2+(1−α)(gt)2
——原来的Adagrad就是,学习率除以的值,就是梯度g0,g1,g2都求平方和,再开根号
——而RMSProp里面也包含了g0,g1,g2,但是你可以有个权重,去选择,你更相信新的梯度还是更相信旧的梯度
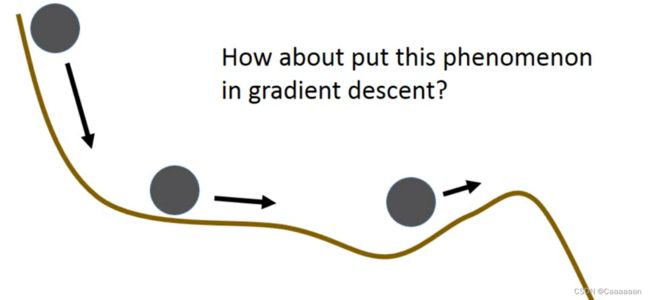
解决非最优问题
- 在plateau非常缓慢
- 在鞍点(saddle point)停了下来
- 在局部最优点(local minima)上停止
-
Yann LeCun(杨立昆)教授的说法是,其实我们不必要太担心局部最优点的问题
-
因为如果它是一个局部最优点,那么它在每一个维度上看上去,都是一个山谷的形状
-
我们假设山谷的形状出现的概率是p,我们假设我们的神经网络有1000个参数,你每一个参数都要呈现山谷的形状,那么这个概率就是 p 1000 p^{1000} p1000
-
因此,在越大的神经网络里面,局部最优点其实没有你想象得那么多;一个很大的神经网络,其实搞不好是很平滑的;
启发式方法解决
- 动量
在现实中,我们丢一个小球,它会具有惯性,使得它可能可以冲过局部最优点,到达这个全局最优的位置
——现在的问题就转换成了,如何把惯性这个东西,引入到我们的神经网络当中
- 我们每一步行走中,不仅仅需要去考虑梯度,而是要将上一次的移动方向加上
- 这样的情况下,梯度并不会让你的行径方向完全转向
—— v i v^i vi实际上是过去所有算出来的梯度的总和
v i = ∇ L ( θ 0 ) + ∇ L ( θ 1 ) + . . . + ∇ L ( θ i − 1 ) v^i=\nabla L(\theta^0)+\nabla L(\theta^1)+...+\nabla L(\theta^{i-1}) vi=∇L(θ0)+∇L(θ1)+...+∇L(θi−1)
——为啥这么说呢?
v 0 = 0 v 1 = − η ∇ L ( θ 0 ) v 2 = − λ η ∇ L ( θ 0 ) − η ∇ L ( θ 1 ) . . . v^0=0\\ v^1=-\eta\nabla L(\theta^0)\\ v^2=-\lambda\eta\nabla L(\theta^0)-\eta\nabla L(\theta^1)\\ ... v0=0v1=−η∇L(θ0)v2=−λη∇L(θ0)−η∇L(θ1)...
——只是先前的梯度的和的权重,受 λ \lambda λ的影响
- 如果你觉得先前的更重要,那么 λ > 1 \lambda>1 λ>1
- 反之小于1
那么RMSProp+Momentum=Adam
测试集表现不好
——建立在训练集上已经表现得不错的情况下
——这种情况属于overfitting,应当想办法提升模型鲁棒性
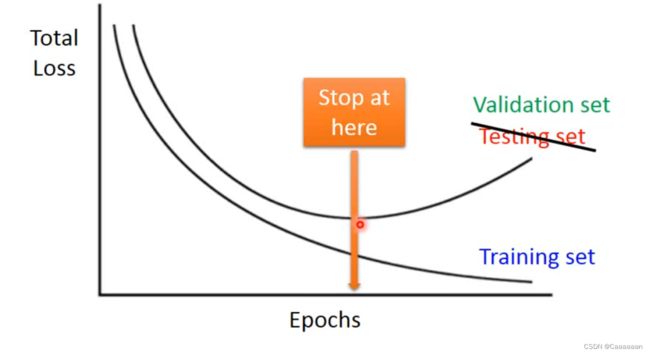
Early Stopping
——这个方法的意思是
当你的学习率合理的时候,你的training set上的loss值应该是逐渐减少的
但是,随着你训练集上loss值的降低,你的测试集的loss值说不准会升高
——因此,应该在测试集loss值最小处就停止train,而不是一直train下去
但是,事实上,我们并不能知道测试集的loss走向,因此,我们用交叉验证来得到这个东西
正则化
L2正则化
——给定义的loss function加上正则项
L ′ ( θ ) = L ( θ ) + λ 1 2 ∥ θ ∥ 2 L'(\theta)=L(\theta)+\lambda\frac{1}{2}\|\theta\|_2 L′(θ)=L(θ)+λ21∥θ∥2
L 2 n o r m ∥ θ ∥ 2 = w 1 2 + w 2 2 + . . . L2\,\,\,norm\\ \|\theta\|_2=w_1^2+w_2^2+... L2norm∥θ∥2=w12+w22+...
—使用L2 norm的式子,称为L2正则化
梯度: ∂ L ′ ∂ w = ∂ L ∂ w + λ w 梯度:\\ \frac{\partial L'}{\partial w}=\frac{\partial L}{\partial w}+\lambda w\\ 梯度:∂w∂L′=∂w∂L+λw
U p d a t e 参数 w t + 1 → w t − η ∂ L ′ ∂ w w t + 1 → w t − η ( ∂ L ∂ w + λ w ) = ( 1 − η λ ) w t − η ∂ L ∂ w Update参数\\ w^{t+1}\rightarrow w^t-\eta\frac{\partial L'}{\partial w}\\ w^{t+1}\rightarrow w^t-\eta(\frac{\partial L}{\partial w}+\lambda w)\\ =(1-\eta\lambda)w^t-\eta\frac{\partial L}{\partial w} Update参数wt+1→wt−η∂w∂L′wt+1→wt−η(∂w∂L+λw)=(1−ηλ)wt−η∂w∂L
—— 1 − η λ 1-\eta\lambda 1−ηλ 的值一般很接近1,但是小于1
——这样每次update都会使得你的值越来越小,可能越来越靠近0
——因为在L2正则化,我们通常会使得参数每次更新都变小一点,因此这招也叫“Weight Decay”
——在深度学习这方面,正则化这件事并不能变现得非常显著,因为正则化这件事保证的就是,你的参数不会离0太远
- 但是在深度学习里,训练网络的时候,我们的初始值往往设置地很小,从某种程度上,减少update次数和正则化做的事情是非常相似的
- 它不像在SVM里面这么重要,因为SVM实质上求解的是一个凸优化函数,所以在实际中,它解的时候不一定会有迭代的这个过程
L1的正则化
∥ θ ∥ 1 = ∣ w 1 ∣ + ∣ w 2 ∣ + . . . \|\theta\|_1=|w_1|+|w_2|+... ∥θ∥1=∣w1∣+∣w2∣+...
L ′ ( θ ) = L ( θ ) + λ 1 2 ∥ θ ∥ 1 L'(\theta)=L(\theta)+\lambda\frac{1}{2}\|\theta\|_1 L′(θ)=L(θ)+λ21∥θ∥1
梯度: ∂ L ′ ∂ w = ∂ L ∂ w + λ s g n ( w ) 梯度:\\ \frac{\partial L'}{\partial w}=\frac{\partial L}{\partial w}+\lambda sgn(w)\\ 梯度:∂w∂L′=∂w∂L+λsgn(w)
U p d a t e 参数 w t + 1 → w t − η ∂ L ′ ∂ w = w t − η ( ∂ L ∂ w + λ s g n ( w t ) ) = w t − η ∂ L ∂ w − η λ s g n ( w t ) Update参数\\ w^{t+1}\rightarrow w^t-\eta\frac{\partial L'}{\partial w}\\ =w^t-\eta(\frac{\partial L}{\partial w}+\lambda sgn(w^t))\\ =w^t-\eta\frac{\partial L}{\partial w}-\eta\lambda sgn(w^t) Update参数wt+1→wt−η∂w∂L′=wt−η(∂w∂L+λsgn(wt))=wt−η∂w∂L−ηλsgn(wt)
- 我们永远都在删除一个 η λ s g n ( w t ) \eta\lambda sgn(w^t) ηλsgn(wt)
- 如果你的参数是正的,就会减;如果是负的,那就会加一个值,会使得你的参数变大
比较
- L1和L2其实都有在减少这个参数的值,但是L1做得事情是,每次都减去一个固定的值;L2做的事情是乘上一个<1的值
- 如果你的参数非常大的话,在L2就会减得非常快,在L1下降的速度是一样的
- 因此L1中不会保留很多很小的值,依然会存在一些很大的值,相对L2来说,参数分布会比较sparse
Dropout
-
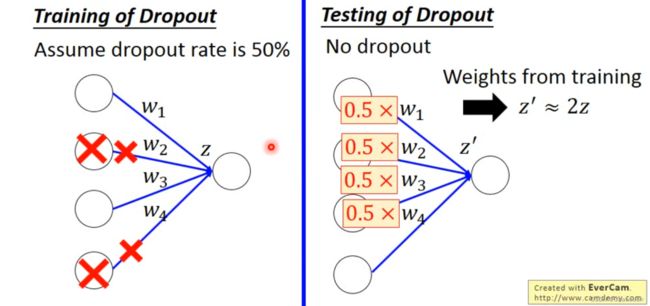
在每次update参数之前
- 每个神经元都有p%的概率被关掉,相关的权重连接也关掉
- 这个时候神经网络的结构会发生改变
- 使用新的神经网络去做训练
-
在train的时候,加上dropout会使得你training的表现变差
-
但是会使得你testing的编写变好
——当你在测试集运行的时候
- 不需要去做dropout
- 如果训练时dropout神经元关闭概率为p%,那么在测试集时,所有的权重都需要乘上(1-p)%
- 比如dropout的p%=50%,如果训练出来权重w=1,那么将w=0.5设置去做测试集
- Dropout是一种ensemble
- 因为你每一次update的时候,网络的结构都是不一样的,因此相当于整合了多个模型
- 但是每个模型之间的参数是共享的