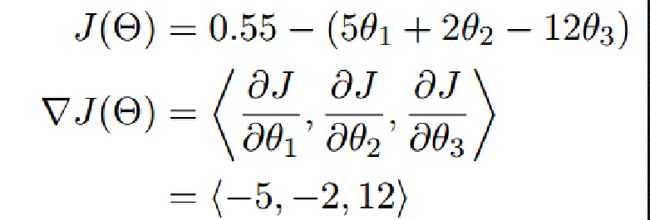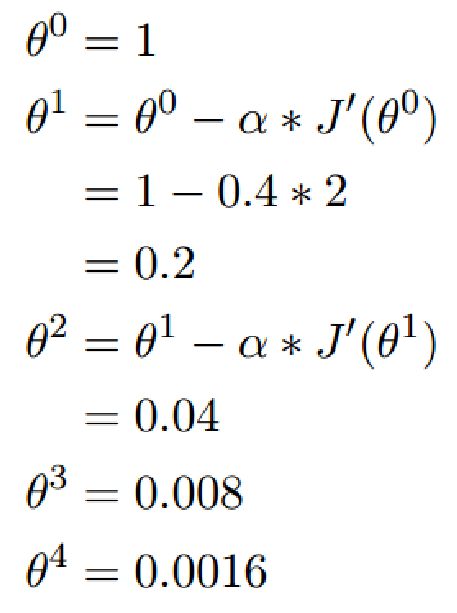BP神经网络(三)--梯度下降法
梯度下降法常用于神经网络负反馈过程中参数的优化。下面对梯度下降法做解释说明。
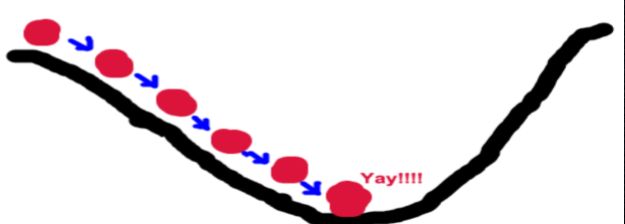
梯度下降法的基本思想可以类比为一个下山的过程。 假设场景:一个人被困在山上,需要从山上下来(i.e. 找到山的最低点,也就是山谷)。 但此时山上的浓雾很大,导致可视度很低。因此,下山的路径就无法确定,他必须利用自己周围的信息去找到下山的路径。这个时候,他就可以利用梯度下降算法来帮助自己下山。
以他当前的所处的位置为基准,寻找这个位置最陡峭的地方,然后朝着山的高度下降的地方走,同理,如果我们的目标是上山,也就是爬到山顶,那么此时应该是朝着最陡峭的方向往上走。然后每走一段距离,都反复采用同一个方法,最后就能成功的抵达山谷。
但是事情没有这么简单,假设这座山最陡峭的地方是无法通过肉眼立马观察出来的, 而是需要一个复杂的工具来测量,此人每走一段距离,都需要一段时间来测量所在位置最陡峭的方向,这是比较耗时的。
那么为了在太阳下山之前到达山底,就要尽可能的减少测量方向的次数。这是一个两难的选择,如果测量的频繁,可以保证下山的方向是绝对正确的,但又非常耗时,如果测量的过少,又有偏离轨道的风险。
结论:需要找到一个合适的测量方向,来确保下山的方向不错误,同时又不至于耗时太多。
导数
导数是一个函数在某一点的导数描述了这个函数在这一点附近的变化率。 几个导数的例子:
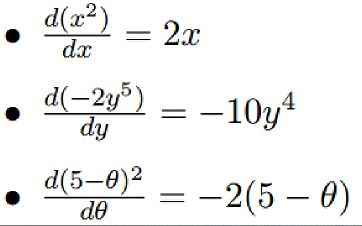
梯度
梯度实质:多变量偏导的一般化,那么求梯度就相当于对各变量求偏导。
在单变量的函数中,梯度其实就是函数的导数,代表着函数在某个给定点的切线的斜率。在多变量函数中,梯度是一个向量,向量有方向,梯度的方向就指出了函数在给定点的上升最快的方。
总结:梯度的方向是函数在给定点上升最 快的方向,那么梯度的反方向就是函数在给定点下降最快的方向,这正是我们所需要的。所以我们只要沿着梯度的方向一直走,就能走到局部的最低点!
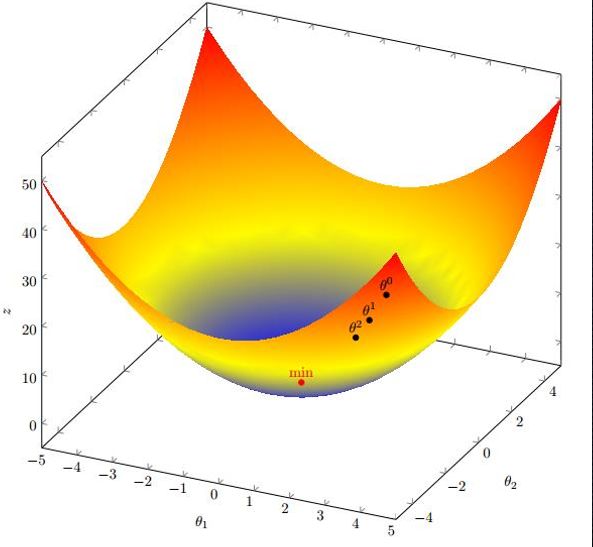
梯度下降法数学解释
J ( θ ) J(\theta) J(θ)是一个可导函数。
θ 1 = θ 0 − α Δ J ( θ ) \theta^1 = \theta^0 - \alpha \Delta J(\theta) θ1=θ0−αΔJ(θ)
此公式的意义是: J ( θ ) J(\theta) J(θ)是关于 θ \theta θ的一个函数,我们当前所处的位置为 θ 0 \theta ^0 θ0点,要从这个点走到J的最小值点,也就是山底。首先我们先确定前进的方向,也就是梯度的反向,然后走一段距离的步长,也就是 α \alpha α,走完这个段步长,就到达了 θ 1 \theta^1 θ1这个点!
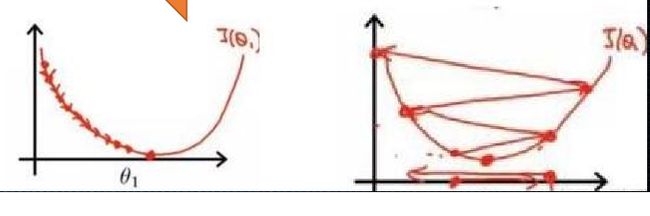
具体解释一下, α \alpha α在梯度下降算法中被称作为学习率或者步长, 意味着我们可以通过 α \alpha α来控制每一步走的距离, 以保证不要步子跨的太大,其实就是不要走太快, 错过了最低点。同时也要保证不要走的太慢,导 致太阳下山了,还没有走到山下.
所以 α \alpha α的选择在梯度下降法中往往是很重要的! α \alpha α设置的过小时,收敛过程将变得十分缓慢。而当学习率 设置的过大时,梯度可能会在最小值附近来回震荡,甚至可能无法收敛。
单变量例子
我们已经基本了解了梯度下降算法的计算过程,那么我们就来看几个梯度下降算法的小实例,首先从单变量的函数开始:
假设有一单变量的函: J ′ ( θ ) = 2 θ J^{'}(\theta) = 2\theta J′(θ)=2θ
学习率为 : $\alpha = 0.4 $
初始值为:1
根据梯度下降公式: θ 1 = θ 0 − α Δ J ( θ ) \theta^1 = \theta^0 - \alpha \Delta J(\theta) θ1=θ0−αΔJ(θ)
我们开始进行梯度下降的迭代计算过程:
经过四次的运算,也就是走了四步,基本就抵达了函数的最低点,也就是山底。
多变量例子
多变量函数的梯度下降:
假设有一个目标函 J ( θ ) = θ 1 2 + θ 2 2 J(\theta) = \theta_1^2+\theta_2^2 J(θ)=θ12+θ22
现在要通过梯度下降法计算这个函数的最小值。我们通过观察就 能发现最小值其实就是 (0,0)点。但是接下来,我们会从梯度下降算 法开始一步步计算到这个最小值!
假设初始的起点为: θ 0 = ( 1 , 3 ) \theta^0=(1,3) θ0=(1,3)
初始的学习率为: α = 0.1 \alpha = 0.1 α=0.1
函数的梯度为: Δ J ( θ ) = ⟨ 2 θ 1 , 2 θ 2 ⟩ \Delta J(\theta) = \left\langle 2\theta_1,2\theta_2 \right\rangle ΔJ(θ)=⟨2θ1,2θ2⟩
经过多次迭代,基本靠近函数的最小值.