【读文献】Generative models for graph-based protein design 蛋白质设计

出处

• 作者：J. Ingraham等
• 机构：MIT
• 期刊：NeurIPS, 2019
• code：https://github.com/jingraham/neurips19-graph-protein-design

摘要

提出了一种给定3D结构，基于图表征的条件生成模型。在蛋白质中，有一类复杂的依赖关系在蛋白质序列上较远但在蛋白质三维结构上是较近的。这篇论文着重强调了他们的方法对这种依赖关系的捕捉能力。

介绍

在Transformer的基础上增补了以图表征的3D分子结构，在多层自注意力结构的组成下，我们的模型能够捕捉序列和结构之间更高层次的、基于交互的依赖关系。基于图结构的序列模型有利于计算效率、归纳偏置（在建模/训练时从数据中所归纳的假设有偏差）和表征的灵活性。
在数以亿计的进化序列上训练的语言模型仍然会被这些序列所代表的数以千计的三维进化折叠在 "语义 "上进行了限制。
我们的模型和图注意力网络很类似，但是我们增加了边特征和一个自回归解码器。

图A：Encoder中是通过在空间上的k个近邻点的多头自注意力来表征3D结构，并且不依靠序列。Decoder是一个自回归模型，在给定整个结构数据和前一个解码的氨基酸来生成下一个氨基酸。图B：Encoder和Decoder的每一层都包含一个邻域聚合（自注意力）和局部信息处理（position-wise ff）的步骤。

Methods

基于Transformer的一个Structured Transformer模型，主要是能够扩展额外的相关信息。
计算成本降低：通常注意力机制会需要二次方的内存以及计算成本，我们通过限制每个节点只需要注意其在3D结构中最近的 k个邻居来避开这个问题。因为结构是多层，所以在迭代局部注意力的时候可以推出该点的全局上下文信息（有点像criss-cross）。
新增额外信息：边特征来embed空间和位置上的关联，使得Transformer在空间结构上具有泛化能力。

图表征结构

结构表示成图，其中$v_N$是每个残基，边$e_{ij}$能够抓住两者之间的关系

这种表示方法可以适应大分子设计问题的不同变化，包括 "刚性骨架 "设计，其中骨架原子的精确坐标是固定的，以及 "柔性骨架 "设计，其中较软的约束可以定义感兴趣的结构。
3D考虑 对于刚体的设计问题，作为条件的结构数据是一组固定的主链坐标

其中，$N$是位置数量。我们希望坐标的图表征有两个属性：

• 不变性。特征具有旋转平移不变性
• 局部的大量信息。由于点$v_i$的邻近点$N(i,k)$入射到点$v_i$的边特征$\{e_{ij}{\}}_{j\in N(i,k)}$，应该包含足够多的信息以至于可以重建所有相邻点的坐标$\{x_j{\}}_{j\in N(i,k)}$。
  不变性是出于标准的对称性考虑，而第二个属性则是出于当前图神经网络的限制。

在这个网络中，更新点$v_i$仅依赖于边和邻近的点特征。然而，一般情况这些特征都是不足以去重建相对的邻居坐标$\{x_j{\}}_{j\in N(i,k)}$。所以独立地更新不能完全依赖于局部环境。比如：在推理坐标$x_i$周围的邻域时，成对的距离$D_{ia}$和$D_{ib}$将不足以确定$x_a$和$x_b$是在同一侧还是在对侧。
相对空间编码 我们通过对点$x_i$增加朝向$O_i$来帮助实现不变性和局部信息特征，其中$O_i$定义了每个点的局部坐标系统（图2A）

图2A：空间特征捕捉到不同折叠的结构关系。 边特征能捕捉主链上两个位置的相对距离、方向和导向。为了可扩展性，所有在初始化稠密欧式距离计算（右上）之后的计算，比如说相对方向（右下）等，都会被限制在k近邻图。
我们在主链几何学方面将其定义为（这就是一个坐标系，每个点都会有这样的坐标系）

（三者分别为单位面向量，单位方向向量和单位朝向向量）其中$b_i$是射线$(x_{i-1}-x_i)$和$(x_{i+1}-x_i)$之间的夹角的负平分线，$n_i$是那个平面的单位向量，所以我们能得到：

最终我们从刚体变化中得到一个空间边特征$e_{ij}^{(s)}$，这个特征可以将$(x_i,O_i)$的参考系和$(x_j,O_j)$的参考系联系起来。

最后可以分解成三个特征：距离、方向、朝向。第一个向量是一个欧氏距离编码。第二个向量是一个方向，编码了在$(x_i,O_i)$参考系下$x_j$的相对方向。第三个向量是朝向，编码了空间旋转矩阵的四元数表征。
相对位置编码 和原始的Transformer一样，我们也使用了位置编码来表示序列中氨基酸之间的距离。具体来说，我们需要表示每个邻居j相对于考虑中的节点i的位置。因此，我们通过$i-j$之间的间隙的正弦函数来嵌入位置信息。我们会保留$i-j$的符号，因为蛋白质序列通常是对称的。
节点和边特征 最终我们通过拼接结构编码$e_{ij}^{(s)}$和位置编码$e_{ij}^{(p)}$得到边向量$e_{ij}$，然后通过线性变换得到和模型一样的维度。在后续所有实验中，我们只会包括k=30的近邻的边信息。这个k=30相较于典型的残基与其小于20个aa的残基相联系的定义来说还比较大。
对于点特征，我们计算三个蛋白质主链的二面角（φi , ψi , ωi），并且计算相应的sin和cos值做embedding。
灵活主链特征 我们还考虑了基于拓扑学二元边缘特征和粗略的主链几何的三维结构的 "灵活骨架 "描述。我们将相对位置编码与两个二元边缘特征结合起来：当i和j处的Cα残基之间的距离小于8埃时表示接触，氢键是有方向的，由DSSP的静电模型定义。对于粗略的节点特征，我们计算主干Cα残基之间的虚拟二面角和键角，将其解释为球面坐标，并将其表示为单位球上的点。

Structured Transformer

自回归分解 通过给定的3D结构分解了蛋白质序列的分布

其中，条件概率$p(s_i|x,s_{<i})$指的是在位置$i$的氨基酸$s_i$依赖于输入结构$x$以及前序氨基酸们$s_{<i}=\{s_1,\dots ,s_{i-1}\}$. 这些条件是以两个子网为参数的：一个encoder，通过基于结构的节点特征$V(x)$和边特征$\mathrm{E}(x)$来计算一个点的embedding；一个 decoder 在encoder给定的前序序列和结构embedding之后，自回归地预测$s_i$.
Encoder 通过变换${\mathbf{W}}_h:{\mathbb{R}}^{d_v}\mapsto {\mathbb{R}}^d$生成初始的embedding ${\mathbf{h}}_i={\mathbf{W}}_h(v_i)$，其中$v_i$是节点特征，并且$i\in [N]\triangleq \{1,2,\dots N\}$。
Encoder的每一层都会实现一个多头自注意力部分，其中 head $l\in [L]$ 里面都会包含三个可学习的q,k,v（Transformer里面的内容没变），query 是从当前节点$i$（一个氨基酸）衍生出来的，key 和 values是从与邻近节点$j\in N(i,k)$的关系信息$r_{ij}=({\mathbf{h}}_j,{\mathbf{e}}_{ij})$中衍生出来的。然后根据以下几个公式：
$$\begin{gathered} Query:{\mathbf{q}}_i^{(l)}={\mathbf{W}}_q^{(l)}({\mathbf{h}}_i) \\ Key：{\mathbf{z}}_{ij}^{(l)}={\mathbf{W}}_z^{(l)}({\mathbf{r}}_{ij}) \\ Value：{\mathbf{v}}_{ij}^{(l)}={\mathbf{W}}_v^{(l)}({\mathbf{r}}_{ij}) \\ i\in [N],l\in [L] \end{gathered}$$
就可以计算attention $a_{ij}^{(l)}$
$$a_{ij}^{(l)}=\frac{exp(m_{ij}^{(l)})}{{\sum }_{j\prime \in N(i,k)}exp(m_{ij\prime }^{(l)})},where{m}_{ij}^{(l)}=\frac{q_i^{(l{)}^T}{z}_{ij}^{(l)}}{\sqrt{d}}$$
最后再计算每个头的结果
$$h_i^{(l)}=\sum _{j\in N(i,k)}{a}_{ij}^{(l)}{v}_{ij}^{(l)}$$
最后把所有的头都拼接到一起，做一个变换：
$$\Delta h_i=W_{o}Concat(h_i^{(1)},\dots ,h_i^{(L)})$$
这里的公式和Transformer中是一致的。网络结构与原始的Transformer也是一致的。
Decoder 模块结构与encoder是一样的，但是增加了关系信息$r_{ij}$，这样可以知道前序序列的元素信息。和enocder不同的是，keys和values是基于关系信息$r_{ij}=({\mathbf{h}}_j,{\mathbf{e}}_{ij})$衍生的

其中${\mathbf{h}}_j^{(dec)}$是节点$j$在当前decoder层中的embedding，${\mathbf{h}}_j^{(enc)}$是encoder中最后一层的节点$j$的embedding。$g(s_j)$是在节点$j$处氨基酸$s_j$的embedding。拼接和masking过的结构保证只有在$i$之前的$j$位置上的序列信息会传递至$i$。但对于$i\le j$的部分，这个decoder仍然会允许位点$i$参加后续的结构信息。

Training

结构 所有的实验中使用的是三层encoder和decoder，隐藏层的维度是128。
优化 lr和初始化参数都是Transformer中的，dropout 10%，label smoothing 10%，根据验证集的困惑度早停。无条件的语言模型不包括dropout和label smoothing。
数据集 使用的是CATH中蛋白质结构的层次分类。在CATH 4.2 中的所有域中 40% 不冗余的蛋白质，我们获取了长度为500的链，并随机的赋予CATH拓扑分类（CAT code）用于训练、验证和测试（8:1:1）。由于一条链可以包含多个CAT code，我们先去除训练集中冗余的组，在去除验证集中的。最后再移除测试集中CAT与训练集中重叠的数据，并且移除验证集中与测试或者训练集中重叠的链。
最终得到18024 训练集，608验证集和1120测试集，两两都没有CAT重叠。

Results

对于评价结果，由于许多不同的序列可能会有相似的3D结构，这意味着序列相似度不一定要很高；与此同时，单点突变可能会使得蛋白质断裂或者折叠错误，所以说明序列高度相似并不足以证明是一个正确的设计。
所以主要关注三个点：

• likelihood-based，验证生成模型能给出较高可能性的序列的能力
• 原始序列的恢复率，通过比较生成序列和原始序列
• 实验对比，将模型生成的可能性与从头设计的蛋白实验产生的高通数据比较。

我们的模型能够提供更准确和更有效的序列恢复率并在可能性上有更好的统计表现。

Likelihood-based 模型上的数据统计比较

蛋白质困惑度 因为有20个标准氨基酸，所以在氨基酸字母表中是属于均一分布，那么困惑度就是元素的个数。如果根据每个字母在自然情况下的频率？

Pfam是一个蛋白质家族库，主要是依赖于Profile HMM对多序列alignment然后按照家族分类蛋白质。其中一阶profiles被广泛用于蛋白质工程。我们发现在Pfam32中的每个字母的profile的ppl高达11.6,，这表明即使有着很高ppl的模型也可能对功能性蛋白质序列的空间是有用的。
结构的重要性 对比了不基于结构条件的模型之间的差异。独立于结构的语言模型，得到的ppl都位于16-17左右，甚至都不如先前的自然频率。然而以结构为先验条件的模型都有较低的ppl。

在深度profile-based方法上的改进 对比了SPIN2，它给定蛋白质结构，使用深度神经网络和蛋白质序列profile。因为SPIN2需要在一个小蛋白质上花费分钟级别的计算，并且是使用这个蛋白作为训练（而不是链），我们在我们的测试集中选取了两个子集，一个是长度在100以内的；一个是原本就只包含单链的蛋白质数据。两个子集都剔除了那些有缺失的氨基酸链。结果是我们的Structured Transformer更好。
图表征和注意力机制 基于图表示的蛋白质设计可以适用于不同的问题，只要用不同的图去建模即可（扩展性好）。在刚性主链（有着更准确的几何细节）和基于空间关联以及氢键的灵活的拓扑设计方面，我们也做了不同的测试。（消融实验）

我们发现增加了局部的朝向信息是比只有距离信息效果好的。
除此之外还修改了信息传递的聚合方法，发现简单的聚合函数表现更好。其中$MLP(\cdot )$是一个两层感知机，不过为什么是两个$h_j$。

我们猜测是因为注意力机制过拟合。虽然表明未来还有提升空间，后续的实验我们还是基于多头注意力机制。

蛋白质重设计的Benchmarking

解码策略 生成蛋白质序列设计需要一个采样机制来帮忙从模型结果中获取高度可能性的序列。beam-search和top-k是常用的启发式方法，但是我们发现从温度修改的分布中使用简单的偏差采样（biased sampling）就足够到比原始序列更好可能性的序列。

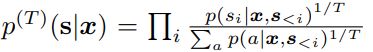
我们在验证集中使用温度$T=0.1$。
与Rosetta对比 为验证我们模型生成的序列的真实性，我们做了两个与Rosetta的对比实验。发现我们的不仅更快也更准确。

第一个实验中，Rosetta 3.10 使用的测试集是我们的单链测试集，用的是固定主链设计协议和默认参数。第二个实验中基于40个多样性的蛋白质，和Rosetta社区中前沿的benchmark做比较。这个实验中我们重新划分了训练集和测试集，使得没有与这40个序列重叠。虽然训练集从_18,000降到10,000条链，但是我们的模型还是在准确率比Rosetta好。

实验性蛋白质设计的无监督异常检测

我们还可以通过比较我们的结构条件语言模型对最近的高通量设计实验中的功能性和非功能性突变蛋白质所赋予的可能性来衡量我们对蛋白质功能的 “了解”。这可以被看作是一种进化的无监督的异常检测。我们与最近的一个高通量设计和诱变实验进行了比较，在该实验中，几个从头设计的小蛋白质被系统地诱变为所有可能的点突变。我们发现，我们模型的对数可能性不可逆转地反映了所设计蛋白质的突变偏好（表5）。

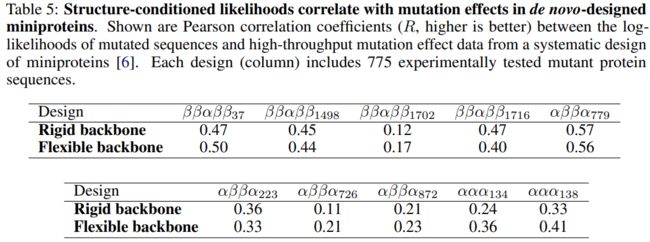
重要的是，我们看到性能不依赖于精确的三维几何特征（如距离和方向），也可以用粗略的信息（如接触、氢键和粗略的骨架角）来实现。

结论

我们引入了一个新的生成模型，用于设计基于其三维结构的图形表示的蛋白质序列。我们的模型用基于图形的三维结构编码增强了Transformer的传统序列级自注意力，并能够利用分子结构中依赖关系的空间定位进行有效计算。当对未见过的折叠进行评估时，我们的模型比最近的基于神经网络的生成模型取得了明显改善的困惑度，并且生成的序列比最先进的程序Rosetta具有更好的准
确性和速度。
我们的框架表明有可能用结构指导的深度生成模型有效地设计和设计蛋白质序列，并强调了生物序列中稀疏、长程依赖关系建模的核心作用。