【论文阅读】Towards Certified Robustness of Distance Metric Learning

1、基本信息

@ARTICLE{9894380,  
author={Yang, Xiaochen and Guo, Yiwen and Dong, Mingzhi and Xue, Jing-Hao},  journal={IEEE Transactions on Neural Networks and Learning Systems},   
title={Toward Certified Robustness of Distance Metric Learning},   
year={2022},  
volume={},  
number={},  
pages={1-11},  
doi={10.1109/TNNLS.2022.3199902}}

2、摘要

度量学习的主要目的在于：将相似实例拉到一起，将不相似的实例分隔开。本文提出在输入数据集空间中引入对抗间隔（adversarial margin）以提高度量学习算法的泛化性（指机器学习算法对新鲜样本的适应能力）与鲁棒性。

对抗间距为实例与离其最近的不同类别的实例之间的距离。它不仅考虑了特征空间中实例间距离，也考虑了metric与triplet constraints之间的关联。为了增强对实例扰动（instance perturbation）的鲁棒性，可以通过增大对抗间隔来实现。最后，利用算法鲁棒性的理论技术证实了增大对抗间隔有利于提高泛化能力。

3、方法

3.1 马氏距离

Mahalanobis Distance是度量学习中一种常用的距离指标，可以看作是欧氏距离的一种修正，修正了欧式距离中各个维度尺度不一致且相关的问题（如：计算身高体重，差10mm的身高与差10kg的体重是完全不同的。但在普通的欧氏距离中，这将会算作相同的差距）。计算公式为：
$$d_M(x_i,x_j)=\sqrt{(x_i-x_j{)}^{T}M(x_i-x_y)}\text{\hspace{1em}(1)}$$
其中，$M$为半正定矩阵（positive semidefinite (PSD) matrix），亦称“度量矩阵”。矩阵中每个非0元素代表不同维度属性的重要性权重。$M$矩阵可通过学习确定，而度量学习则是对该矩阵进行学习。由于PSD的特性，矩阵$M$可以分解为$L^{T}L$。因此计算马氏距离相当于是通过$L$矩阵线性的将实例由原始输入空间转化到特征空间后，再在特征空间中计算实例间的欧氏距离$||L{x}_i-L{x}_j|{|}_2$ 。

如矩阵$M$是单位向量，也就是各维度独立同分布，马氏距离就变成了欧氏距离。

3.2 引入对抗间隔的缘由

假设$x_i$是一个实例，$x_j$与$x_l$分别是它最近的同类实例与异类实例。许多基于三元组的算法（如LMNN）的约束为：
$$f(x_i):=d_M^2(x_i,x_l)-d_M^2(x_i,x_j)\ge 1\text{\hspace{1em}(2)}$$

在度量学习中，当上述约束条件成立时，$x_i$就能够通过最近邻分类器(Nearest Neighbor Classifier，NN classifier)成功分类。

约束（2）式最右方的1表示在实例级别上的单位间隔（unit margin），为的是避免训练集中的小噪声数据。

由于上述的常规方法无法处理实例扰动（instance perturbation）问题，因此本文提出最大化对抗边界。对抗边界为实例$x_i$与距其最近的不同类实例间的距离，而这种实例（adversarial example）就可以视为是$x_i$的一个扰动点$x_i+△x_i$，且$f(x_i+△x_i)<0$。

若实例$x_i$的所有adversarial example都远离它，那么就不存在$△x_i$，就能得到高度的健壮性。基于此，我们可以找到$x_i$最近的adversarial example，并将它推开。

3.3 对抗间隔的推导

给定训练实例$x_i$与其相关的三元组约束$(x_i,x_j,x_l)$，目标是找到落在特征空间中由$x_j$和$x_l$组成的决策边界上的距离$x_i$最近的点$x_{i,min}$，即对抗样本。

$$\begin{gathered} x_{i,min}=\underset{{x_i}^{\prime }\in {\mathbb{R}}^p}{\mathrm{argmin}}({x_i}^{\prime }-x_i{)}^T({x_i}^{\prime }-x_i) \\ s.t.(L{x_i}^{\prime }-\frac{L{x}_j+L{x}_l}{2}{)}^T(L{x}_l-L{x}_j)=0\text{\hspace{1em}(3)} \end{gathered}$$

（3）式在input space中定义了一个平面，旨在通过欧式距离找到离$x_i$最近的且满足约束条件（落在$x_j$与$x_l$的决策边界（平面）上）的对抗样本。

利用拉格朗日乘子法，可以找到$x_{i,min}$的显式公式：
$$x_{i,min}=x_i+\frac{(\frac{x_j+x_l}{2}-x_i)M(x_l-x_j)}{(x_l-x_j{)}^T{M}^2(x_l-x_j)}M(x_l-x_j)\text{\hspace{1em}(4)}$$

找到了对抗样本$x_{i,min}$后，我们就能够计算$x_i$与$x_{i,min}$之间的欧氏距离平方：
$$d_E^2(x_i,x_{i,min})=\frac{(d_M^2(x_i,x_l)-d_M^2(x_i,x_j){)}^2}{4d_{M^2}^2(x_j,x_l)}\text{\hspace{1em}(5)}$$
我们称$d_E(x_i,x_{i,min})$为对抗间距，它代表了对子空间中扰动的最大容忍量。

3.4 与传统方法的对比

局部泛化：不考虑所有样本间的区别，只考虑样本与其对抗样本$x_{i,min}$（领域内类别不同的样本）应如何分开。

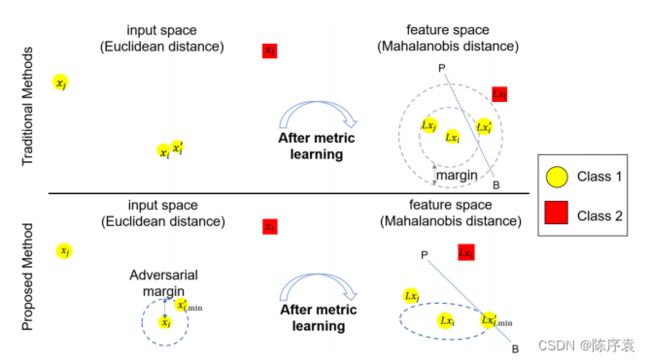
传统方法：将相同类别的实例对($x_i$,$x_j$)与不同类别的实例对（$x_i$,$x_l$）通过间隔分开。当$x_j$为$x_i$的最近邻时，能够成功预测。但由于在input space中，距离对于干扰十分敏感，一些细微的干扰会使得$x_i$变为${x_i}^{\prime }$，近邻误判为$x_l$，并因此产生错误预测分类。

本文的方法：旨在扩大对抗间隔（adversarial margin），对抗间隔等于实例$x_i$与其最近的对抗样本$x_{i,min}$之间的欧氏距离。