Chapter1-4_Speech_Recognition(HMM)

本文为李弘毅老师【Speech Recognition - HMM (optional)】的课程笔记，课程视频youtube地址，点这里(需)。其中也涉及到了部分李琳山老师关于HMM的详解（讲得非常清楚，请务必先搞懂HMM，再看这篇）。

下文中用到的图片均来自于李宏毅老师和李琳山老师的PPT，若有侵权，必定删除。

文章索引：

上篇 - 1-3 CTC, RNN-T and more

下篇 - 1-5 Alignment of HMM, CTC and RNN-T

总目录

1 HMM用在哪里

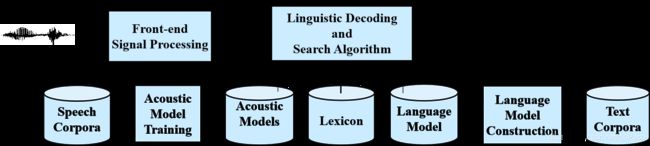
没有深度学习的语音识别系统可以用下面这幅图来表示，不过很多用到深度学习的也基本是把其中的一些模块替换调成了DNN而已。要输出一段声音信号，得到对应的文字，需要四个东西：

• 声音特征(Feature Vectors)。这个我们之前也有提到过，忘了的可以看下这里，一般会用一个叫做MFCC的方法，把声音信号转化成长度为$T$，特征维度为39维的向量。
• 声学模型(Acoustic Models)。这里是用到HMM(Hidden Markov Model)的地方，就是输入Feature Vectors，得到每个Feature Vector对应的state是什么，而这里的state一般是指比Phoneme(发音的基本单元，比如th-ih-s-ih-z-s-p-ih-ch)更小的基本单元。
• 词典(Lexicon)。用来把声学模型得到的一串state转换成对应的单词，比如(th-ih-s) → this。
• 语言模型(Language Model)。这个就是把得到的单词变成一个完整通顺的句子的模型。

我们这篇主要讲的就是这个声学模型(Acoustic Models)，其他的部分暂时不去关心。

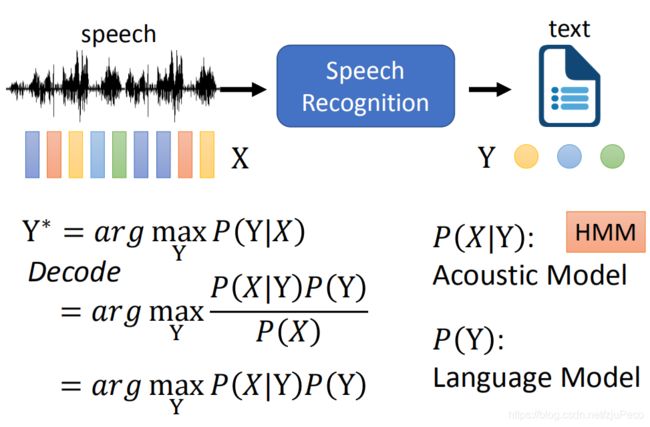
上面这个是李琳山老师的说法，李弘毅老师讲的更抽象一些，但本质是一样的。如下图所示，比如我们有一个模型可以计算给定声音信号$X$，得到输出序列$Y$的概率$P(Y|X)$，那么我们只需要遍历所有的$Y$，然后找到使得$P(Y|X)$的概率最大的那个$Y$就可以了。但是，$Y$的可能性太多了，这样的计算消耗太大了，这个方案，这里不讨论。

学过贝叶斯定理的都知道，这个条件概率是可以变一变的，经过如下图所示的变化后，我们只需要找到一个$Y$，使得$P(X|Y)P(Y)$最大就可以了，而这里的$P(X|Y)$就是我们的声学模型(Acoustic Models)，这里的$P(Y)$就是我们的语言模型(Language Model)，$P(X)$和我们要找的$Y$没有关系，可以直接扔掉。有时$P(Y)$也可以不用考虑。而这里的$P(X|Y)$可以用很机智的演算法去求解。

其实李弘毅老师讲的$P(X|Y)$就是李琳山老师讲的声学模型(Acoustic Models)和词典(Lexicon)的结合。

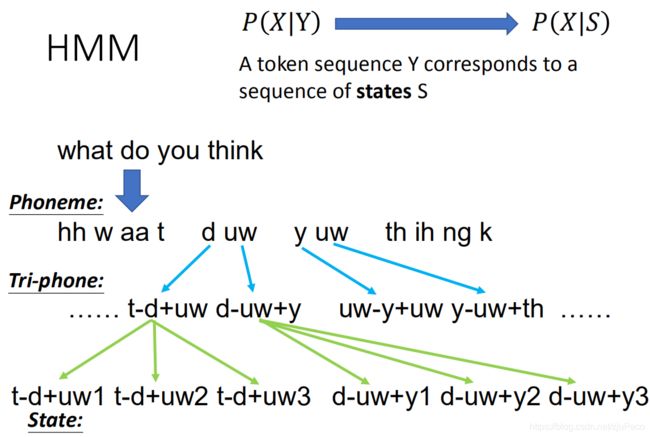
2 HMM的state

HMM里需要一个叫做state的东西，如上文所述，它在我们的声学模型里，就是一个比Phoneme更小的东西，那它究竟有多小呢？答案就是，它可以任意小，只要我们的计算资源足够就可以。首先，Phoneme会根据上下文被拆分成Tri-phone，Tri-phone就是说，我们今天的"uw"的这个音在不同的上下文中是不一样的，可以是"d-uw+y"的"uw"，也可以是"y-uw+th"的"uw"，把句子中前一个Phoneme和后一个Phoneme都加进来，就变成了Tri-phone。而我们的state比Tri-phone还要小，一个Tri-phone可以拆成多个state，这个state人已经无法分辨了，具体要拆成几个state，就看我们的计算资源有多少了。

为什么要拆的这么小呢？因为在计算HMM的时候，我们希望人在发出每个state所对应的音的时候，是可以用高斯混合模型(GMM)去模拟它的分布的，而不同的人说同一个词时，发出的音时不一样的，所以希望这个state可以代表非常细的音。

所有的$Y$都可以转换成state，所以，我们我们今天要求的$P(X|Y)$，就可以转变为求$P(X|S)$。

可以想象，按这种做法的话，我们的state会非常多，比如Phoneme有30个，最后把每个Tri-phone再切成3个单元的话，我们将会有$30^3\times 3$个state。这意味着什么？Emmm~这意味着我们要很多的高斯混合模型(GMM)。我们先来讲下HMM的计算中需用到的几个概率函数。

计算HMM的时候，我们需要知道三个概率，一个叫做转移概率(Transition Probability)，一个叫做发射概率(Emission Probability)，还有一个叫做初始概率(initial state probabilities)。李弘毅老师在讲的时候没有提到初始概率，那我们就默认是所有的state初始概率都是相等的吧。

• 转移概率：从一个state变到任意另一个state的概率。
• 发射概率：每个state产生该time step对应的特征向量的概率，如$P(X^1|"t-d-uw1")$。
• 初始概率：最开始从某个state开始的概率。

其中的发射概率就是说我们的每个state都要有一个高斯混合模型(GMM)，也就是我们要$30^3\times 3$个GMM！更难处理的是，有些state在数据中出现的是很少的，我们称为rare state，很难学好。这个时候，一种方法是把这些rare state映射到其他相近的state的GMM上，另一种就是2010年提出的Subspace GMM。Subspace GMM这里简单说一下，就是说我们现在所有的state都有一个公用的池子(Pool)，每个state要计算发射概率的时候，从Pool里捞几个GMM出来就可以了。

好，现在假设我们已经有了转移概率和发射概率，但我们仍旧无法把$P(X|S)$计算出来，因为我们并不知道每个$X^i$是由哪个state产生的。李弘毅老师说，states的个数往往小于声音特征向量$X$的长度。因此，如果按顺序用完所有的state的话，可以有很多条路径，HMM做的就是把所有路径的概率加起来。

这个从路径对应到特征向量的操作，就叫做对齐(alignment)。这个在下节课会详细介绍。

3 改造成DNN

3.1 Tandem

Tandem没有改变原来的整套方案，只是在对于输入的特征进行了一个分类，使得每个time step的acoustic feature都有预测出来的对应于每一个state的概率。然后把这个DNN的输出当作新的acoustic feature，再放进原来的模型里去跑就可以了。

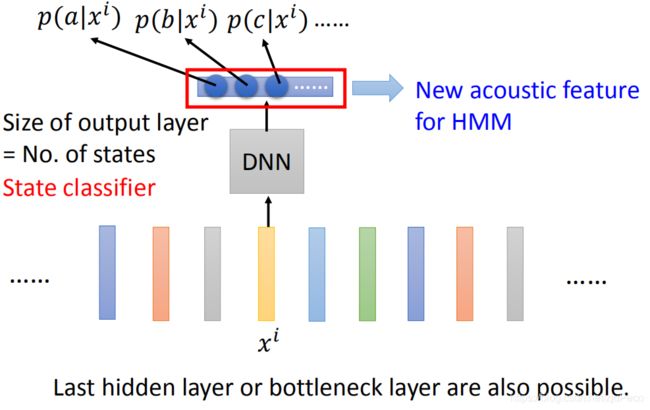
3.2 DNN-HMM Hybrid

HMM里面是有一个GMM的模型的，也就是上文所说的发射概率的计算模型。DNN-HMM Hybrid就是把这个GMM模型换成了DNN去做。DNN可以是CNN或者LSTM这些。

之前GMM模型是计算出$P(x|a)$，也就是给定state $a$发射出特征$x$的概率。现在的DNN能计算$P(a|x)$，也就是给定特征$x$，则$x$是state $a$的概率。然而，这两个东西不一样呀。于是就需要用条件概率转换一下，得到
$$P(x|a)=\frac{P(a|x)P(x)}{P(a)}$$

然后这里，$P(a|x)$就是DNN的输出，$P(a)$可以从数据中统计出来，$P(x)$不用去管它。。。

为什么要用DNN来替换GMM呢？有人认为$P(x|a)$是generative learning，而$P(a|x)$是discriminative learning，然后大家认为后者比较厉害，这样。也有人认为DNN的参数比较多，比较厉害，这样。而实际证明，这种方法，很强。

我仔细想了下，感觉这个和Tandem的区别其实并不大。它们其实都是要有一个DNN的state classifier。

不过，这个state classifier怎么train呢？我们都知道，trainDNN的模型是需要标签的，然而我们并不知道现在的$X^i$分别属于哪一个state。这该咋办？实际操作的时候，用了类似于半监督的方法，就是利用HMM+GMM来train一个模型，然后拿这个train好的模型的结果来当作标签去train这个DNN的模型。然后再把train的DNN的结果当作标签，训练一个新的DNN，一直反复这样下去。这样的方法很强，train出来的模型结果和人类接近！