Matlab数字图像处理学习记录【7】——形态学图像处理

一.预备知识

1.1 集合论中的基本概念

简单来说，如果将一幅图像看做一个映射：f是为每对不同坐标(x,y)分配亮度值的映射，则f(x,y)称为数字图像。
比如A是Z²中的一个集合，其中的元素是像素坐标(x,y).若w=(x,y)是A的一个元素，那么可以写为：w∈A。同样，若w不是A的元素，则可以写为：w∉A。满足特殊条件的像素坐标集合B可以写成: B={w|condition} 又或者所有像素均不属于集合A，记为A^c， 则A^c={w|w∉A}。该集合是集合A的补集。记为C＝A∪B。
同理可得：交集A∩B和差集A-B。
同时，形态学通常还要有两个运算符。B的映像：$\hat{B}=w|w=-b，b\in B$
集合A对于点z的平移：z=(z₁,z₂)： (A)_z={c|c=a+z,a∈A}

1.2 二值图像、集合和逻辑运算符

数集合的运算也能应用于二值图像集合。比如，A和B是二值图像，则C=A∪B仍是一幅二值图像。若A和B中相应的像素是前景像素。则C中像素也是前景像素，则函数C为：
$$C(x,y)=\{\begin{array}{ll}1& 若A(x,y)或B(x,y)为1或均为1\\ 0,& 其他\end{array}$$
另一方面，按照集合的思想：$C=(x,y)|(x,y)\in A或(x,y)\in B或(x,y)\in (A和B)$
那么在matlab上使用命令进行这些操作的关键字是：

二.膨胀与腐蚀

2.1 膨胀

膨胀是二值图像中的“加长”或“变粗”的操作。这种特殊的方式有一个称为“结构元素”的集合控制。
假设这是这个是原图像：

而这个结构图像是一个长度为5的斜线：

滑动结构图像中心的□与原图像对比，若原图像上□位置上为1，则被结构图像覆盖的地方，在新图上都是1，就如该图所示：

数学上，膨胀的定义为集合运算。A被B膨胀，记为A⊕B，定义为：
$$A\oplus B=z|({\hat{B}}_z\cap A\ne \varnothing )$$
其中,∅为空集，B为结构元素。总之，A被B膨胀是所有结构元素原点位置组成的集合，其中映射并平移后的B至少与A的某些部分重叠。这种在膨胀过程中对结构元素的平移类似于卷积。
一般来说，把A作为操作数，B作为结构元素，而且，结构元素往往比操作数小得多。
matlab里用imdilate函数

A = imread('./add.tif');
B = [0 1 0; 1 1 1; 0 1 0];
out = imdilate(A, B);
subplot(1,2,1);
imshow(A);
subplot(1,2,2);
imshow(out);

2.2 结构元素的膨胀

膨胀满足结合律，即：
A⊕(B⊕C)=(A⊕B)⊕C
总而言之，A先与B膨胀，再与C膨胀，等同于，B与C先膨胀再与A膨胀。
假设B=B₁⊕B₂
又有
A⊕B = A⊕(B₁⊕B₂) = (A⊕B₁)⊕B₂)
那么假设我们让A与一个5×5的结构元素膨胀，等同于与一个1×5和5×1的结构元素膨胀。


后者能有效的减小运算次数，从而使得膨胀运算能够更快的计算完成。

2.3 strel函数

通过se = strel(shape， parameters)可以构造出多种形状的元素。但它返回的是一个特殊的strel对象。推测其内部可能是由稀疏矩阵构成。使用该函数可以加快膨胀运算的速度。


例如：

se = strel('diamond', 4)
-----
strel is a diamond shaped structuring element with properties:
      Neighborhood: [9×9 logical]
    Dimensionality: 2

2.4 腐蚀

腐蚀类似于膨胀，而腐蚀则为将滑动结构图像中心的□与原图像对比，若原图像上□位置上为0，则被结构图像覆盖的地方，在新图上都是0。
记作

f = imread('.\example.tif');
subplot(1,2,1);
imshow(f);
se = strel('disk', 10);
sub = imerode(f, se);
subplot(1,2,2);
imshow(sub);

三. 腐蚀和膨胀的组合

3.1 开运算与闭运算

开运算可记为:

或

表示A被B腐蚀后再用B来膨胀的结果。
形态学开运算完全删除了不能包含结构元素的对象区域,平滑了对象的轮廓，断开了狭窄的连接,去掉了细小的突出部分。
闭运算是先膨胀再腐蚀，记作

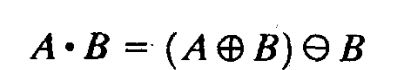
闭运算一般会将狭窄的缺口连接起来形成细长的弯口，并填充比结构元素小的洞
该图例较好的表示了开闭运算的效果：

开闭运算可以用该两句代码实现：
C = imopen(A, B) 和 C = imclose(A, B)
该图可以说明开闭运算的效果：

通过这个指纹，我们可以看到 先开运算再闭运算后的效果：

f = imread('.\fingerprint.tif');
subplot(1,3,1);
imshow(f);
subplot(1,3,2);
se = strel('square', 3);
fo = imopen(f, se);
imshow(fo);
subplot(1,3,3);
foc = imclose(fo, se);
imshow(foc);

3.2 击中和击不中变换

通常，能够识别像素的特定形状是很有用的,例如孤立的前景像素或者是线段的端点像素。
其中，B是结构元素对B =(B,，B.)，而不是单个元素。击中或击不中变换由这两个结构元素定义为：

该变换可以在用该函数实现：C= bwhitmiss (A, B1, B2)
比如举个定位方块左上角元素的方法：

f = imread('.\left.tif');
subplot(1,2,1);
imshow(f);
subplot(1,2,2);
b1 = strel([0 0 0; 0 1 1; 0 1 1]);
b2 = strel([1 1 1; 1 0 0; 1 0 0]);
g = bwhitmiss(f, b1, b2);
imshow(g);

3.3 查找表

在击中或击不中结构元素较小时，用查找表LUT的方法更快。
查找表的思想和哈希表的思想差不多，通过一个矩阵，将3×3的矩阵映射为一个2⁹以内的一个唯一整数。有位操作那味儿。
将图像中的3×3与该矩阵相乘，并将乘积加起来。
例如：
$$\left|\begin{array}{ccc}1& 8& 64\\ 2& 16& 128\\ 4& 32& 256\end{array}\right|\times \left|\begin{array}{ccc}1& 1& 0\\ 1& 0& 1\\ 1& 0& 1\end{array}\right|$$
则 计算结果为1(1)+2(1)+ 4(1)+8(1)+ 16(0) + 32(0)+ 64(0) + 128(1) + 256(1)= 399。
工具箱提供两个函数makelut和applylut(将在本节稍后说明),这两个函数可用于实现这种技术。函数makelut基于一个提供给用户的函数构造一个查找表，函数applylut则使用这个查找表来处理二值图像。
编写函数endpoints

function g = endpoints(f)
%ENDPOINTS Computes end points of a binary image.
%   G = ENDPOINTS(F) computes the end points of the binary image F
%   and returns them in the binary image G. 

%   Copyright 2002-2004 R. C. Gonzalez, R. E. Woods, & S. L. Eddins
%   Digital Image Processing Using MATLAB, Prentice-Hall, 2004
%   $Revision: 1.3 $  $Date: 2003/04/22 01:18:18 $

persistent lut

if isempty(lut)
   lut = makelut(@endpoint_fcn, 3);
end

g = applylut(f,lut);

%-------------------------------------------------------------------%
function is_end_point = endpoint_fcn(nhood)
%   Determines if a pixel is an end point.
%   IS_END_POINT = ENDPOINT_FCN(NHOOD) accepts a 3-by-3 binary
%   neighborhood, NHOOD, and returns a 1 if the center element is an
%   end point; otherwise it returns a 0. 

is_end_point = nhood(2,2) & (sum(nhood(:)) == 2);

f = imread('.\left.tif');
subplot(1,2,1);
imshow(f);
subplot(1,2,2);
g = endpoints(f);
imshow(g);

也可以获得类似的图案：

3.4 bwmorph函数

该函数可以基于膨胀、腐蚀、查找表操作的组合实现多种有用的操作。其参数有以下选择：

比如细化则是将二值物体和形状减小为单个像素宽的线。
比如，这样细化指纹一次或两次：

f = imread('.\fingerprint.tif');
se = strel('square', 3);
f = imopen(f, se);
f = imclose(f, se);
subplot(1,3,1);
imshow(f);
subplot(1,3,2);
g1 = bwmorph(f, 'thin', 1);
imshow(g1);
subplot(1,3,3);
g2 = bwmorph(f, 'thin', 2);
imshow(g2);

或者将细化次数设置为Inf，让它迭代到图像收敛：

f = imread('.\fingerprint.tif');
se = strel('square', 3);
f = imopen(f, se);
f = imclose(f, se);
subplot(1,2,1);
imshow(f);
subplot(1,2,2);
g1 = bwmorph(f, 'thin', Inf);
imshow(g1);

四.标注连接分量

迄今为止,我们讨论过的概念主要适用于所有前景(或背景)的单个像素及与相邻像素。本节将分析单个前景像素和所有前景像素集合之间的重要“部分”。这就引入了连接分量的概念，在下面的讨论中,连接分量也称为对象。
比如，这是E的一部分：

图中两块儿1 中间隔了几行0，将E分离开，变成了两个单独的组。而实际上他们都是属于字母E的。所以为开发定位和操作对象的计算机程序,我们需要为关键术语做一系列更为精确的定义。
例如：一个坐标为(x,v)的像素p有两个水平和两个垂直的相邻像素，它们的坐标分别为(x+1,y)，(x -1, y),(x, y + 1)和(x. y- 1)。p的这4个相邻像素的集合记为N₄( p):
同理，如果是对角线的四个元素则被记为N_D( p)。
N₄( p)和N_D( p)的并集记为N₈( p)：

若q∈N₄( p)，则像素p和q称为4邻接。同样，若q∈ N( p)，则p和q称为8邻接。图9.18(d)和图9.18(e)说明了这些概念。p₁和p_n之间的一条路径是一系列像素p₁，p₂，…， p_n-1， p_n。
其中p_k和p_k+1相邻，1≤k
若在前景像素p和q之间存在一条完全由前景像素组成的4连接路径则这两个前景像素称为4连接。若它们之间存在一条8连接路径，则称为8连接。对于任意前景像素p，与其相连的所有前景像素的集合称为包含p的连接分量。
连接分量这一术语是根据路径来定义的,而路径的定义则取决于邻接。这就表明连接分量的性质取决于我们所选的邻接方式，最常见邻接方式为4邻接和8邻接。
使用[L, num] = bwlabel(f, conn)
其中，f是一幅输人二值图像，conn用于指定期望的连接（不是4就是8)。输出L称为标记矩阵，参数num(可选）给出所找到的连接分量的总数。若省略了参数conn，则其值默认为8。每个不同连接分量中的像素被分配给一个惟一的整数，该整数的范围是从1到连接分量的总数。换言之,标记值为1的像素属于第–个连接分量;标记值为2的像素属于第二个连接分量;依次类推。
通过自己编写函数，看看效果：

f = imread('ABCD.tif');
f = im2bw(f);
[L, n] = bwlabel(f);
subplot(2,3,1);
imshow(f);
for i = 1:4
    [r, c] = find(L == i);
    btw = zeros(size(f));
    btw(r,c) = 1;
    subplot(2,3,i+1)
    imshow(btw);
end

五.形态学重构

重构是一种涉及到两幅图像和一个结构元素（而不是单幅图像和一个结构元素)的形态学变换。一幅图像，即标记(marker )，是变换的开始点。另一幅图像是掩模(mask)，用来约束变换过程。结构元素用于定义连接性。
若g是掩膜，f为标记，则从f重构g可以记为R_g(f)，它的迭代过程如下：

1. 将h₁初始化为图像f
2. 创建结构元素B = ones(3)
3. 重复：h_k+1 = (h_k⊕B)∩g。直到h_k+1=h_k

其中标记f一定要是g的子集。f⊆g
当然，matlab里用了更快速的“快速混合重构法”，其语法为：out = imreconstruct(maker, mask)：
其效果如下：

5.1 由重构做开运算

在形态学开运算中,腐蚀通常会去除小的对象,而随后的膨胀往往会还原所保留对象的形状。然而，这种还原的精度取决于形状和结构元素之间的相似性。本节所讨论的方法，即由重构做开运算，将准确地恢复腐蚀之后的对象形状。
比如，先通过开运算获得一个竖直长条fe，此时fe是函数f的子集。然后通过fe对f重构，即可获得带竖直长条的字母，而开运算只能获得竖直长条：

f = imread('textbook.tif');
subplot(2,2,1);
imshow(f);
fe = imerode(f, ones(51, 1));
subplot(2,2,2);
imshow(fe);
fo = imopen(f, ones(51, 1));
subplot(2,2,3);
imshow(fo);
fobr = imreconstruct(fe, f);
subplot(2,2,4);
imshow(fobr);

同理，我们将结构元素从(51,1）改为（1,51）即可获得长横条的字母。为了效果，改为(1,30)：

5.2 填充孔洞

假设选择衣服标记图像f_m，该图像的边缘部分的值为1-f，其余部分的值为0
$$f_m(x,y)=\{\begin{array}{ll}1-f(x,y)& \text{若(x,y)在f的边界上}\\ 0& \text{其他}\end{array}$$
可以用函数：g = imfill(f, ‘holes’)进行孔洞填充，后面会对该函数细讲。

5.3 清除图像边界

重构的另一种应用是清除图像中与边界相接触的对象。同样,关键任务仍然是选择合适的标记和掩模图像来达到希望的效果。在这种情况下，我们将原图像用做掩模，且标记图像f_m定义为：
$$f_m(x,y)=\{\begin{array}{ll}f(x,y)& \text{若(x,y)在f的边界上}\\ 0& \text{其他}\end{array}$$
IPT函数imclearborder可自动地执行上面的整个过程。该函数的语法为g = imclearborder(f, conn)
其中，f是输入图像，g是输出。conn的值可以是4，也可以是8(默认值)。该函数会去掉比周围对象更亮且与图像边界相连接的结构。输人f可以是一幅灰度图像，也可以是一幅二值图像。相应的输出图像分别是一幅灰度图像或一幅二值图像。

六.灰度图像形态学

6.1 膨胀与腐蚀

使用结构元素b对f的灰度膨胀记为f⊕b定义为：
$$(f\oplus b)(x,y)=max\{f(x-x^{\prime },y-y^{\prime })+b(x^{\prime },y^{\prime })|(x^{\prime },y^{\prime })\in D_b\}$$
其中，D_b是b的定义域，f(x, y)在f的定义域外为假设为-∞。该公式实现类似于空间卷的处理。从概念上讲，我们可以认为结构元素关于其原点旋转并在图像中的所有位置平移,就像卷积核被旋转并在图像上平移那样。在每个平移位置,旋转的结构元素的值与图像像素值相加并计算出最大值。
卷积与灰度膨胀之间的一个重要不同在于:在灰度膨胀情形下，二值矩阵D_b定义了邻域中的哪些位置包括在最大值运算中。换言之，对于D_b的定义域中的任意一对坐标(x₀, y₀)，若在那些坐标处D_b为1，则和式f(x-x₀,y-y₀)+ b(x₀,y₀)包括在最大值计算中。若在(x₀,y₀)处D_b为0，则在最大值运算中就不再考虑这个和式。对于所有坐标(x’,y’)∈ D_b，每次坐标(x, y)变化时均重复该过程。若绘制出坐标x’和y’的函数b(x’,y’)的图形，则该图形看起来会是一幅数字“表面图”，其在任意一对坐标处的高度由这些坐标处的b值给出。
实际上，灰度膨胀通常使用平坦的结构元素（见表9.2）来执行，这种结构元素中，b的值在D_b的定义域内的所有坐标处均为0，即
$$b(x^{\prime },y^{\prime })=0,(x^{\prime },y^{\prime })\in D_b$$
在这种情况下，最大值运算完全由二值矩阵D_b中的0和1模式来指定，且灰度膨胀公式可简化为:
$$(f\oplus b)(x,y)=max\{f(x-x^{\prime },y-y^{\prime })|(x^{\prime },y^{\prime })\in D_b\}$$
因此，平坦的灰度膨胀是一个局部最大值算子，其中的最大值取自由D_b的形状所确定的一系列像素邻域。
非平坦算子由b = strel([1 1 1], [1 2 1]);创建，将创建一个大小为1×3的结构元素，该元素的高度值为b(0, -1)= 1，b(0,0)= 2，b(0,1)=1。
平坦算子可以由strel('square', 3)创建。
这里给出例子：

f = imread('scenery.tif');
subplot(1,3,1);
imshow(f);
b = strel([1 1 1], [1 5 1]);
fb = imdilate(f, b);
subplot(1,3,2);
imshow(fb);
c = strel('square', 3);
display(c.Neighborhood);
fc = imdilate(f, c);
subplot(1,3,3);
imshow(fc);

同理，腐蚀的话记为f⊖b，定义为：
$$(f\ominus b)(x,y)=min\{f(x-x^{\prime },y-y^{\prime })-b(x^{\prime },y^{\prime })|(x^{\prime },y^{\prime })\in D_b\}$$
与膨胀一样，灰度腐蚀通常使用平坦的结构元素来执行。平坦的灰度腐蚀公式可以简化为：
$$(f\ominus b)(x,y)=min\{f(x-x^{\prime },y-y^{\prime })|(x^{\prime },y^{\prime })\in D_b\}$$
其他的同腐蚀：

f = imread('scenery.tif');
subplot(1,3,1);
imshow(f);
b = strel([1 1 1], [1 5 1]);
fb = imerode(f, b);
subplot(1,3,2);
imshow(fb);
c = strel('square', 3);
display(c.Neighborhood);
fc = imerode(f, c);
subplot(1,3,3);
imshow(fc);

`膨胀和腐蚀可以组合使用,以例获得各种效果。例如,从膨胀后的图像中减去腐蚀过的图像可产生一个“形态学梯度”，它是检测图像中局部灰度级变化的一种度量。例如:

f = imread('scenery.tif');
subplot(1,4,1);
imshow(f);
c = strel('square', 3);
subplot(1,4,2);
fb = imdilate(f, c);
imshow(fb);
subplot(1,4,3);
fc = imerode(f, c);
imshow(fc);
subplot(1,4,4);
morph_grad = imsubtract(fb, fc);
imshow(morph_grad);

6.2 开运算和闭运算

灰度图的开运算和闭运算的定义和二值图像的表达式相同。而几何意义是：
假设一幅图像函数f(x,y)可看做是一个三维表面;换言之,其亮度值解释为xy平面上的高度值。然后，b对f的开运算可以解释为结构元素b沿表面f的下沿向上移动，并移过f的整个定义域。在结构元素沿f的底面滑动时，通过找到结构元素的任何部分所能到达的最高点，就可构建开运算。
图9.24示例了一维情形下的这种概念。图9.24(a)所示的曲线是一幅图像中的单行取值。图9.24(b)在曲线下方显示了平坦的结构元素。完整的开运算在图9.24©中显示为沿着阴影区域顶部的曲线。由于结构元素太大而不能匹配曲线中间的峰值,所以开运算删除了该峰值。一般来说,开运算用来去除小的亮点，同时保持所有的灰度级和较大的亮区特性相对不变。
图9.24(d)给出闭运算的图形示例。注意，结构元素位于曲线的上方，并沿曲线平移到了所有位置。图9.24(e)显示了闭运算后的结果,其构建方式是当结构元素在曲线的上方滑动时,找到结构[素的任何部分所能到达的最低点。其中，我们看到闭运算去除了比结构元素更小的暗色细节。
这个图例就非常清晰明了：

比如这是一个灰度形态学运算的例子：

f = imread('plus.tif');
se = strel('disk', 5);
fo = imopen(f, se);
foc = imclose(fo, se);
subplot(1,3,1);
imshow(f);
subplot(1,3,2);
imshow(fo);
subplot(1,3,3);
imshow(foc);

亦或者顶帽变换。开运算可用于补偿不均匀的背景亮度。一幅米粒图像f,图像下部的背景要比上部的背景黑。对这样不均匀的亮度做阈值处理很困难。但是经阙值处理后的图像,图像顶部的米粒已被很好地从背景中分离开来,但图像底部的米粒并未从背景中正确地提取出来。对图像进行开运算可以产生对整个图像背景的合理估计,只要结构元素大到不能完全匹配米粒即可。没找到合适的图，就用书上例子代替了：

6.3 重构

灰度级形态学重构和前面给出的相同迭代过程定来定义。下图显示了一维情形下重构的工作方式。图a中的顶部曲线是掩模，底部的灰色曲线则是标记。这种情况下，标记由掩模减去一个常量形成。但是，通常情况下，任何信号都可以用做标记，只要不超过掩模板中的相应值即可。重构过程的每一次迭代都扩展了标记曲线的峰值,直到被掩模曲线强制压下为止[见图(b)]
最终的重构是图©中的黑线。注意,重构中两个较小的峰值被消除了,但高一些的两个峰虽然被削弱了一些,但还是得到了保留。当一幅标记图像是由一幅掩模图像减去一个常量h得到的时，该重构就称为h极小值(h-minima)变换。由IPT函数imhmin计算的h极小值变换可用于抑制小峰值。

另一个有用的灰度级重构技术是开运算重构(opening-by-reconstruction)，在这种重构中，一幅图像首先被腐蚀，就像在标准的形态学开运算中一样。但是，若使用闭运算代替开运算，则这幅被腐蚀的图像在图像重构中将用做标记图像。原图像将用做掩模。图9.29(a)显示了开运算重构的一个例子，它是使用如下命令实现的:

f = imread('disk.tif');
se = strel('disk', 5);
fe = imerode(f, se);
fobr = imreconstruct(fe, f);
subplot(1,2,1);
imshow(f);
subplot(1,2,2);
imshow(fobr);

通过应用一种称为闭运算重构(closing-by-reconstruction)的技术，可进一步清理图像fobr。闭运算重构是通过对一幅图像求补、计算其开运算重构并对结果求补来实现的。步骤如下所示:

f = imread('disk.tif');
se = strel('disk', 5);
fe = imerode(f, se);
fobr = imreconstruct(fe, f);
subplot(2,2,1);
imshow(f);
subplot(2,2,2);
imshow(fobr);
fobrc = imcomplement(fobr);
fobrce = imerode(fobrc, se);
fobrcbr = imcomplement(imreconstruct(fobrce, fobrc));
subplot(2,2,3);
imshow(fobrc);
subplot(2,2,4);
imshow(fobrcbr);

书中还举了通过重构删除复杂图像的背景这个例子：
我们的最后示例将在几个步骤中使用灰度级重构。我们的目的是要突显出如图所示的计算器键盘上的文字。第一步是消除每个键上方的水平反射光。为了达到这个目的，将利用这些反射比图像中的任何文本字符都要宽的这个事实。我们使用一个结构元素(一条长水平线）来执行开运算重构:
代码：

f = imread('calc.tif');
f_obr = imreconstruct(imerode(f, ones(1, 71)), f);
f_o = imopen(f, ones(1, 71));
f_thr = imsubtract(f, f_obr);
f_th = imsubtract(f, f_o);
g_obr = imreconstruct(imerode(f_thr, ones(1, 11)), f_thr);
g_obrd = imdilate(g_obr, ones(1, 21));
f2 = imreconstruct(min(g_obrd, f_thr), f_thr);
imshow(f2);
subplot(3,3,1);
imshow(f);
title('原图像a')
subplot(3,3,2);
imshow(f_obr);
title('对原图像a开运算重构的图像b')
subplot(3,3,3);
imshow(f_o);
title('对原图像a进行标准开运算的图像c')
subplot(3,3,4);
imshow(f_thr);
title('对原图像顶帽重构后的图像d')
subplot(3,3,5);
imshow(f_th);
title('对原图标准顶帽后的图像e')
subplot(3,3,6);
imshow(g_obr);
title('对图像d使用水平线开运算重构的图像f')
subplot(3,3,7);
imshow(g_obrd);
title('对f使用水平线膨胀后的图像')
subplot(3,3,8);
imshow(f2);
title('最终图像')