【数学建模】2021年中国高校大数据挑战赛A题
2021年中国高校大数据挑战赛——A题
10月28日早上8点拿到题目——11月1日20点提交
<4天时间><国二>
开源:https://github.com/Ralphson/CBDC_2021
1. 异常检测
利用附件的指 标数据,对所有小区在上述三个关键指标上检测出这29 天内共有多少个异常数值,其中异常数值包含以下两种情况:异常孤立点、异常周期。
-
标准化,使用的是**
Max-Min标准化**X = X − X . m i n ( ) X . m a x ( ) − X . m i n ( ) X = \frac{X - X.min()}{X.max()-X.min()} X=X.max()−X.min()X−X.min()
-
小波变换:得到的主周期就是
时间周期; -
<异常检测常用算法>
-
箱型图:对输入数据的上、下四分位点根据比例计算其上界和下界,处于界外的点被视为异常点;
u p L i m i t = Q 3 + 1.5 ∗ ( Q 3 − Q 1 ) d o w n L i m i t = Q 3 − 1.5 ∗ ( Q 3 − Q 1 ) \begin{aligned} upLimit = Q3+1.5*(Q3-Q1)\\ downLimit = Q3-1.5*(Q3-Q1)\\ \end{aligned} upLimit=Q3+1.5∗(Q3−Q1)downLimit=Q3−1.5∗(Q3−Q1) -
LOF异常检测:这是一个类似密度的聚类算法,对我们一维的时间序列不好做检测,我们为它添加时间轴后强行使用检测算法发现效果并不好,异常点分布并不明显还不如相信图;
-
LOF异常检测
用视觉直观的感受一下,对于 C 1 C_1 C1集合的点,整体间距,密度,分散情况较为均匀一致,可以认为是同一簇;对于 C 2 C_2 C2集合的点,同样可认为是一簇。 o 1 o_1 o1、 o 2 o_2 o2点相对孤立,可以认为是异常点或离散点。现在的问题是,如何实现算法的通用性,可以满足 C 1 C_1 C1和 C 2 C_2 C2这种密度分散情况迥异的集合的异常点识别。LOF可以实现我们的目标。
![]()
-
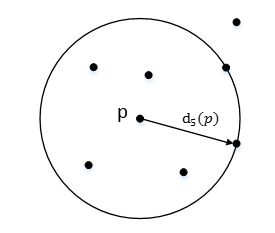
d(p, o):两点 P P P和 O O O之间的距离
-
K-distance:第k距离
在距离数据点 p p p最近的几个点中,第k个最近的点跟点 p p p之间的距离称为点 p p p的K-邻近距离,记为 K − d i s t a n c e ( p ) K-distance(p) K−distance(p)。
对于点 p p p的第k距离 d k ( p ) dk(p) dk(p)定义如下:
d k ( p ) = d ( p , o ) dk(p)=d(p, o) dk(p)=d(p,o)并且满足:
(a)在集合中至少有不包括 p p p在内的k个点 o ∈ C x ≠ p o∈C{x≠p} o∈Cx=p,满足 d ( p , o ′ ) ≤ d ( p , o ) d(p,o')≤d(p,o) d(p,o′)≤d(p,o)
(b)在集合中最多不包括 p p p在内的k-1个点 o ∈ C x ≠ p o∈C{x≠p} o∈Cx=p,满足 d ( p , o ′ ) ≤ d ( p , o ) d(p,o')≤d(p,o) d(p,o′)≤d(p,o)
p p p的第k距离,也就是距离 p p p第k远的点的距离,不包括 p p p,如下图所示:
-
k-distance neighborhood of p p p:第k距离邻域
点 p p p的第k距离邻域 N k ( p ) N_k(p) Nk(p)就是 p p p的第k距离即以内的所有点,包括第k距离。
因此 p p p的第k邻域点的个数 ∣ N k ( p ) ∣ > = k |N_k(p)| >=k ∣Nk(p)∣>=k
-
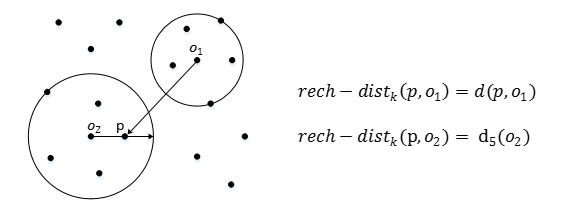
reach-distance:可达距离
可达距离的定义跟K-邻近距离是相关的,给定参数k时,数据点 p p p到数据点 o o o的可达距离 r e a c h − d i s t ( p , o ) reach-dist(p, o) reach−dist(p,o)为数据点 o o o的K-邻近距离和数据点 p p p与点 o o o之间的直接距离的最大值。
点 o o o到点 p p p的第k可达距离定义为:
reach − distance k ( p , o ) = max { k − distance ( o ) , d ( p , o ) } \operatorname{reach}-\operatorname{distance}_{k}(p, o)=\max \{k-\operatorname{distance}(o), d(p, o)\} reach−distancek(p,o)=max{k−distance(o),d(p,o)}
也就是,点 o o o到点 p p p的第k可达距离,至少是 o o o的第k距离,或者为 o o o, p p p之间的真实距离。这也意味着,离点 o o o最近的k个点, o o o到他们的可达距离被认为是相等,且都等于 d k ( o ) d_k(o) dk(o)。如下, o 1 o_1 o1到 p p p的第5可达距离为 d ( p , o 1 ) d(p, o1) d(p,o1), o 2 o_2 o2到 p p p的第5可达距离为 d 5 ( o 2 ) d_5(o2) d5(o2) -
local reachablity density:局部可达密度
局部可达密度的定义是基于可达距离的,对于数据点 p p p,那些跟点 p p p的距离小于等于K-distance§的数据点称为它的K-nearest-neighbor,记为 N k ( p ) N_k(p) Nk(p),数据点 p p p的局部可达密度为它与邻近的数据点的平均可达距离的倒数。
点 p p p的局部可达密度表示为:
lrd k ( p ) = 1 / ( ∑ o ∈ N k ( p ) reach − dist k ( p , o ) ∣ N k ( p ) ∣ ) \operatorname{lrd}_{k}(p)=1 /\left(\frac{\sum_{o \in N_{k}(p)} \operatorname{reach}-\operatorname{dist}_{k}(p, o)}{\left|N_{k}(p)\right|}\right) lrdk(p)=1/(∣Nk(p)∣∑o∈Nk(p)reach−distk(p,o))
表示点 p p p的第k邻域内点到 p p p的平均可达距离的倒数。注意:是 p p p的邻域点 N k ( p ) N_k(p) Nk(p)到 p p p的可达距离,不是 p p p到 N k ( p ) N_k(p) Nk(p)的可达距离,一定要弄清楚关系。
并且,如果有重复点,那么分母的可达距离之和有可能为0,则会导致 l r d lrd lrd变为无限大,下面还会继续提到这一点。这个值的含义可以这样理解,首先这代表一个密度,密度越高,我们认为越可能属于同一簇,密度越低,越可能是离群点,如果 p p p和周围邻域点是同一簇,那么可达距离越可能为较小的 d k ( o ) d_k(o) dk(o),导致可达距离之和较小,密度值较高;如果 p p p和周围邻居点较远,那么可达距离可能都会取较大值 d ( p , o ) d(p, o) d(p,o),导致密度较小,越可能是离群点。
-
local outlier factor:局部离群因子
根据局部可达密度的定义,如果一个数据点根其他点比较疏远的话,那么显然它的局部可达密度就小。但LOF算法衡量一个数据点的异常程度,并不是看他的绝对局部密度,而是它看跟周围邻近的数据点的相对密度。这样做的好处是可以允许数据分布不均匀,密度不同的情况。局部异常因子既是用局部相对密度来定义的。数据点 p p p的局部相对密度(局部异常因子)为点 p p p的邻居们的平均局部可达密度跟数据点 p p p的局部可达密度的比值。
点 p p p的局部离群因子表示为:
L O F k ( p ) = ∑ o ∈ N k ( p ) lrd k ( o ) lrd k ( p ) ∣ N k ( p ) ∣ = ∑ o ∈ N k ( p ) lrd k ( o ) ∣ N k ( p ) ∣ / lrd k ( p ) L O F_{k}(p)=\frac{\sum_{o \in N_{k}(p)} \frac{\operatorname{lrd}_{k}(o)}{\operatorname{lrd}_{k}(p)}}{\left|N_{k}(p)\right|}=\frac{\sum_{o \in N_{k}(p)} \operatorname{lrd}_{k}(o)}{\left|N_{k}(p)\right|} / \operatorname{lrd}_{k}(p) LOFk(p)=∣Nk(p)∣∑o∈Nk(p)lrdk(p)lrdk(o)=∣Nk(p)∣∑o∈Nk(p)lrdk(o)/lrdk(p)
表示点 p p p的邻域点 N k ( p ) N_k(p) Nk(p)的局部可达密度与点 p p p的局部可达密度之比的平均数。LOF主要通过计算一个数值score来反映一个样本的异常程度。这个数值的大致意思是:一个样本点周围的样本点所处位置的平均密度比上该样本点所在位置的密度。如果这个比值越接近
1,说明 p p p的其邻域点密度差不多, p p p可能和邻域同属一簇;如果这个比值越小于1,说明 p p p的密度高于其邻域点密度, p p p为密度点;如果这个比值越大于1,说明 p p p的密度小于其邻域点密度, p p p越可能是异常点。
算法流程
- 1,对于每个数据点,计算它与其他所有点的距离,并按从近到远排序
- 2,对于每个数据点,找到它的K-Nearest-Neighbor,计算LOF得分
注:
LOF 算法中关于局部可达密度的定义其实暗含了一个假设,即:不存在大于等于k个重复的点。当这样的重复点存在的时候,这些点的平均可达距离为零,局部可达密度就变为
无穷大,会给计算带来一些麻烦。在实际应用中,为了避免这样的情况出现,可以把 K-distance改为 K-distinct-distance,不考虑重复的情况。或者,还可以考虑给可达距离都加一个很小的值,避免可达距离等于零。 LOF算法需要计算数据点两两之间的距离,造成整个算法时间复杂度为O(n**2)。为了提高算法效率,后续有算法尝试改进。FastLOF(Goldstein, 2012)先将整个数据随机的分成多个子集,然后在每个子集里计算LOF值。对于那些LOF异常得分小于等于1的。从数据集里剔除,剩下的在下一轮寻找更合适的nearest-neighbor,并更新LOF值。这种先将数据粗略分为多个部分,然后根据局部计算结果将数据过滤减少计算量的想法,并不罕见。比如,为了改进 K-Means的计算效率,Canopy Clustering算法也采用过比较相似的做法。
代码:
import numpy as np
from sklearn.neighbors import LocalOutlierFactor as LOF
import matplotlib.pyplot as plt
# generate train data
X_inliers = 0.3 * np.random.randn(100, 2)
X_inliers = np.r_[X_inliers + 2, X_inliers - 2]
# generate some outliers
X_outliers = np.random.uniform(low=-4, high=4, size=(20, 2))
X = np.r_[X_inliers, X_outliers]
n_outliers = len(X_outliers) # 20
ground_truth = np.ones(len(X), dtype=int)
ground_truth[-n_outliers:] = -1
# fit the model for outlier detection
clf = LOF(n_neighbors=20, contamination=0.1)
# use fit_predict to compute the predicted labels of the training samples
y_pred = clf.fit_predict(X)
n_errors = (y_pred != ground_truth).sum()
X_scores = clf.negative_outlier_factor_
plt.title('Locla Outlier Factor (LOF)')
plt.scatter(X[:, 0], X[:, 1], color='k', s=3., label='Data points')
# plot circles with radius proportional to thr outlier scores
radius = (X_scores.max() - X_scores) / (X_scores.max() - X_scores.min())
plt.scatter(X[:, 0], X[:, 1], s=1000*radius, edgecolors='r',
facecolors='none', label='Outlier scores')
plt.axis('tight')
plt.xlim((-5, 5))
plt.ylim((-5, 5))
plt.xlabel("prediction errors: %d"%(n_errors))
legend = plt.legend(loc='upper left')
legend.legendHandles[0]._sizes = [10]
legend.legendHandles[1]._sizes = [20]
plt.show()
2. 标签预测
针对问题1检测出的异常数值,通过该异常数值前的数据建立预测模型,预测未来是否会发生异常数值。异常预测模型除了考虑模型准确率以外,还需要考虑两点:1)模型输入的时间跨度,输入数据的时间跨度越长,即输入数据量越多,模型越复杂,会增加计算成本和模型鲁棒性,降低泛化能力;2)模型输出时间跨度,即预测的时长,如果只能精准预测下一个时刻是否发生异常,在时效性上则只能提前一个小时,时效性上较弱。
-
Stacking:一层使用高斯过程分类、随机森林、支持向量机、梯度提升决策树训练;二层使用随机森林训练。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ifw2DFpE-1650681131201)(D:\资料\笔记\image\stacking.png)]
注:首先第一层对训练集5折,生成子训练集和验证集,每一折使用子训练集训练,使用验证集预测,将验证集得到的预测结果横向累计;同样,对测试集进行预测,将测试集的预测结果横向加权平均。
第二层使用一个简单的模型,如线性回归、RF等,将第一层得到的结果视为训练集和测试集,将原始数据视为训练标签和测试标签,训练模型并预测即可输出预测结果和准确度。
-
GridSearchCV:一个sklearn的调参接口,给它分类器模型和调参范围便可以自动调参,这个函数是遍历枚举;相应的,RandomSearchCV则是纯随机的手段,对每个变量采用随机采样和等概率采样抽取。
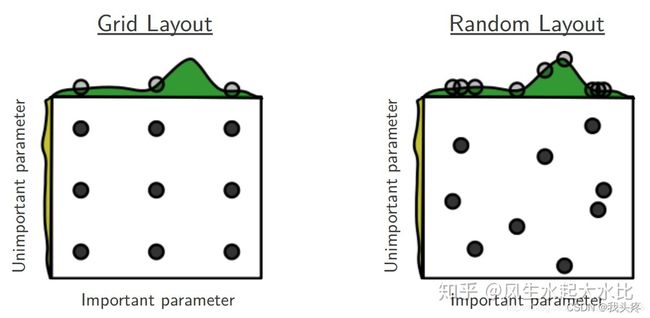
注:横轴纵轴分别代表一个参数分布,两种调参方式都选取9个点,可以看到随机的方式取得的点的分布在这种情况下优于矩阵调参。
3. 趋势预测
利用2021 年8 月28 日0 时至9 月25 日23 时已有的数据,预测未来三天(即9 月26 日0 时-9 月28 日23 时)上述三个指标的取值。并完整填写附件2 中的预测值表格,单独上传到竞赛平台。
LSTM网络:
- 网络结构:
class Net(torch.nn.Module):
def __init__(self):
super(Net, self).__init__()
self.k = 16
self.lstm1 = nn.LSTM(3, self.k, num_layers=2, batch_first=True)
self.sigmod = nn.Sigmoid()
self.linear2 = nn.Linear(self.k * ipt_size, 3 * opt_size)
def forward(self, ipt):
x, (h, c) = self.lstm1(ipt)
x = self.sigmod(x)
x = x.reshape(-1, self.k * ipt_size)
x = self.linear2(x)
return x
注:Train维度是(8,72,3),分别表示8个时间窗,每个时间窗是24*3的数据条数,每条数据包含3个维度;
Test维度是(8,216),分别表示8个时间窗,每个窗中的数据被flatten,也是同样的三天的72条数据*3个维度
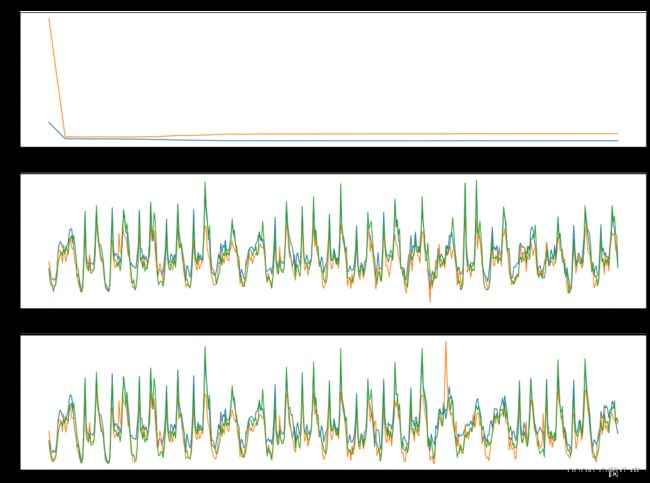
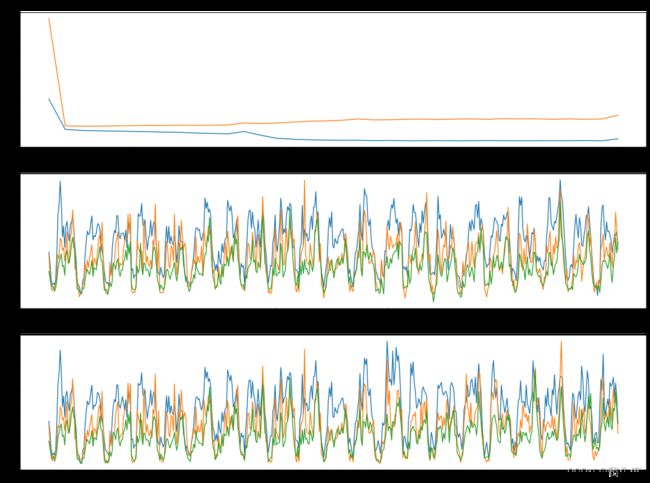
注:1. 网络仅仅是简单堆叠而成,状态量h、c都没用上,应该改进;2. 网络隐层宽度感觉不够,但是增加k之后效果出现下降,不知为何;
- 训练过程:
torch.cuda.empty_cache()
model = Net().to(device)
cost = torch.nn.MSELoss()
optimizer = torch.optim.Adam(model.parameters(), lr=0.001)
def train_cell(cell, df):
losses = []
x_train, y_train, x_test, y_test, _= make_dataset3(df, 24)
model.train()
bar = tqdm(range(1800)) # batch次数
for i in bar:
pred = model(x_train)
loss = cost(pred, y_train)
optimizer.zero_grad()
loss.backward()
optimizer.step()
if i % 50 == 0:
test_loss = cost(model(x_test), y_test)
bar.set_description('loss:{} test_loss:{}'.format(loss.data.float().cpu(), test_loss.data.float().cpu()))
losses.append([loss.data.float().cpu(), test_loss.data.float().cpu()])
print(i, loss, test_loss)
结果有过拟合,但是隐层节点也不多,batchsize也不大;同时train和test的损失都有分离的情况,说明模型有点不契合。