MATLAB利用小波分析提取周期

参考文章：

形象易懂讲解算法I——小波变换

信号分析的主要目的是寻找一种简单有效的信号变换方法，使信号包含的重要特征能显示出来。
在小波变换兴起之前，Fourier级数展开和Fourier分析是刻画函数空间、求解微分方程、进行数学计算的有效方法和有效的数学工具。
从物理直观上看，一个周期性振动的量可以看成是具有简单频率的简谐振动的叠加。Fourier级数展开则是这一物理过程的数学描述。

一.Fourier变换

Fourier变换基本原理

傅里叶变换把无限长的三角函数作为基函数：

这个基函数会伸缩、会平移（其实本质并非平移，而是两个正交基的分解）。
缩得窄，对应高频；伸得宽，对应低频。然后这个基函数不断和信号做相乘。某一个尺度（宽窄）下乘出来的结果，就可以理解成信号所包含的当前尺度对应频率成分有多少。于是，基函数会在某些尺度下，与信号相乘得到一个很大的值，因为此时二者有一种重合关系。那么我们就知道信号包含该频率的成分的多少。

仔细体会可以发现，这一步其实是在计算信号和三角函数的相关性。


这两种尺度能乘出一个大的值（相关度高），所以信号包含较多的这两个频率成分，在频谱上这两个频率会出现两个峰。
以上，就是粗浅意义上傅里叶变换的原理。

Fourier变换实例

举例如下：

fun = @(t) cos(2*pi*10*t)+cos(2*pi*25*t)+cos(2*pi*50*t)+cos(2*pi*100*t);
x = 0:0.001:1;
y = fun(x);
Dfy = fft(y);                 % 离散Fourier变换
Dfy_shift = fftshift(Dfy); % 对称变换得到对称的Fourier频谱
figure
plot(y); axis([0,1000,-3,4]),xlabel('x'),ylabel('y');     % 原始平稳信号

figure
plot(abs(Dfy)),axis([0,250,0,600]),xlabel('n'),ylabel('|Dfy|');               % |Dft|为离散频谱幅值信息

相应具体图像如下：

做完FFT（快速傅里叶变换）后，可以在频谱上看到清晰的四条线，信号包含四个频率成分。

Fourier变换对非平稳过程，具有局限性。
下面简单介绍：信号虽具有相同频谱，但具体序列并不相同。

如上图，最上边的是频率始终不变的平稳信号。而下边两个则是频率随着时间改变的非平稳信号，它们同样包含和最上信号相同频率的四个成分。

做FFT后，我们发现这三个时域上有巨大差异的信号，频谱（幅值谱）却非常一致。尤其是下边两个非平稳信号，我们从频谱上无法区分它们，因为它们包含的四个频率的信号的成分确实是一样的，只是出现的先后顺序不同。

可见，傅里叶变换处理非平稳信号有天生缺陷。它只能获取一段信号总体上包含哪些频率的成分，但是对各成分出现的时刻并无所知。因此时域相差很大的两个信号，可能频谱图一样。

Fourier变换是平稳信号分析的最重要的工具。然而在实际运用中，所遇到的信号大多数并不平稳，而是时变频率信号，这时人们需要知道信号在突变时刻所对应的频率成分。

二.短时傅里叶变换（Short-time Fourier Transform, STFT）

1946年诺贝尔奖获得者D.Gabor引入了短时傅里叶变换(Short-time Fourier Transform)，虽然短时傅里叶变换随着窗口在时间轴t上滑动可以抠取频谱上的所有信息，但从本质上讲，短时傅里叶变换是一种单一分辨率的信号分析方法，因为它使用一个固定的短时窗函数（常用Gauss函数），窗口大小缺乏自适应功能，窗口位置可以移动，但是形状不能改变。

通俗理解，“把整个时域过程分解成无数个等长的小过程，每个小过程近似平稳，再进行傅里叶变换，就知道在哪个时间点上出现了什么频率。”这就是短时傅里叶变换。

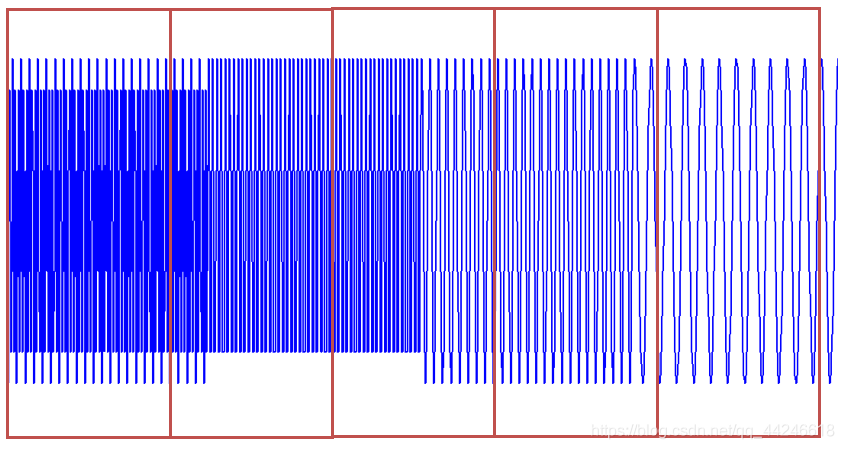
使用STFT存在一个问题，我们应该用多宽的窗函数？窗太宽太窄都有问题：

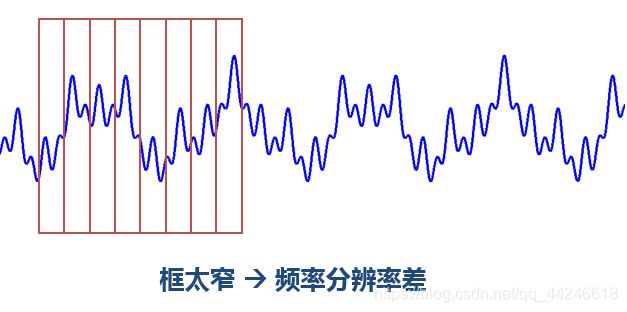
窗太窄，窗内的信号太短，会导致频率分析不够精准，频率分辨率差。

窗太宽，时域上又不够精细，时间分辨率低。

三.小波分析（Wavelet Analysis）

从事石油信号处理的法国工程师J.Morlet在研究地下岩石油层分布时，于1974年首先提出了小波变换的概念，并且J.Morlet构建了光滑柔性的、时频域局部性能都较好的Morlet小波函数。数学家Meyer，Mallat，Daubechies，K.Chui 等人的工作为小波分析的诞生和发展奠定了基础。

小波变换简介

小波变换做出的改变主要是将无限长的三角函数基换成了有限长的会衰减的小波基。

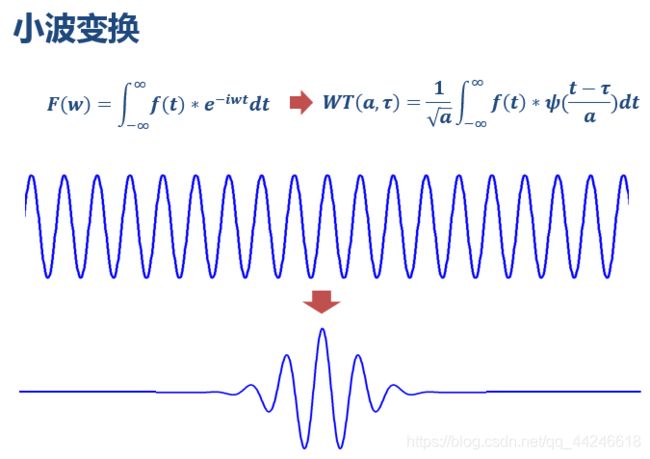
从公式可以看出，不同于傅里叶变换，变量只有频率ω，小波变换有两个变量：尺度a（scale）和平移量 τ（translation）。尺度a控制小波函数的伸缩，对应于频率（反比）；平移量 τ控制小波函数的平移，对应于时间。

当伸缩、平移到这么一种重合情况时，也会相乘得到一个大的值。这时候和傅里叶变换不同的是，这不仅可以知道信号有这样频率的成分，而且知道它在时域上存在的具体位置。

而当我们在每个尺度下都平移着和信号乘过一遍后，我们就知道信号在每个位置都包含哪些频率成分。

小波变换基本原理

两类：
1.连续小波变换CWT
2.离散小波变换DWT

区别： DWT是数据的紧凑表示，对于降噪和数据压缩特别有用，而CWT换对于特征提取更好。

CWT函数

matlab自带的有两种实现方式，一种是2006年版本推出的函数cwt，一种是2016年版本推出的函数cwt。两个函数名称相同，用法不同。

【旧版本】cwt用法为：

coefs = cwt(x,scales,'wname')

用于获取实的或者复的连续小波变换系数，其中“wname”为选取的小波，可以用waveinfo查看小波的相关信息。
举例：

%针对同一个分段函数，采用“Haar“小波分解，得到小波的频谱
fun = @(x)0.*(x<0 |x>5)+x.*(x>=0 & x<1)+1.*(x>=1 & x<4) +(5-x).*(x>=4 & x<5);%分段函数
x=-5:0.2:10;%x自变量
y = fun(x);
figure(1)
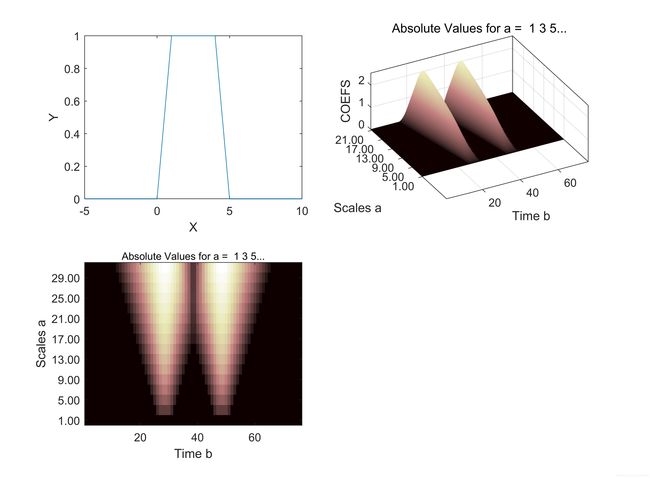
Cab = cwt(y,1:2:32,'haar','3Dplot');%连续小波变换，并进行频谱幅值的三维显示
figure(2)
Cab = cwt(y,1:2:32,'haar','plot');%连续小波变换，并进行频谱幅值的图像显示
%这段程序也可以按照Gabor变换的方式显示，即
a = 1:2:32;
b = 1:length(y);
Cab = cwt(y,1:2:32,'haar');%连续小波变换，并进行频谱幅值的三维显示

【新版本】cwt用法为：

[wt,f] = cwt(x,wname,fs)

最明显的区别在于，新版本取消了自定义尺度函数scales的功能。同时新版本还更新替换了一部分小波函数。
旧版本支持 ‘haar’，‘db’，‘sym’，‘cmor’，‘mexh’，‘gaus’，‘bior’等小波，新版本支持’morse’， 'amor’和 'bump’小波。

常见小波基函数

目前我们主要是通过用小波分析方法处理信号的结果与理论结果的误差来判定小波基的好坏，由此决定小波基。
常用小波基有Haar小波、Daubechies(dbN)小波、Mexican Hat(mexh)小波、Morlet小波、Meyer小波等。
1.Haar小波
Haar函数是小波分析中最早用到的一个具有紧支撑的正交小波函数，也是最
简单的一个小波函数，它是支撑域在[0,1]∈t范围内的单个矩形波。
Haar小波的时域和频域波形如下：

[phi,g1,xval]=wavefun('haar',20);

subplot(2,1,1);
plot(xval,g1,'LineWidth',2);
xlabel('t')
title('haar 时域');
g2=fft(g1);
g3=abs(g2);

subplot(2,1,2);
plot(g3,'LineWidth',2);
xlabel('f')
title('haar 频域')

2.Morlet小波
连续复小波变换
Morlet小波的时域和频域波形图：

d=-6;
h=6;
n=100;
[g1,x]=morlet(d,h,n);

subplot(2,1,1);
plot(x,g1,'LineWidth',2);
xlabel('t');
title('morlet 时域');
g2=fft(g1);
g3=(abs(g2));

subplot(2,1,2);
plot(g3,'LineWidth',2);
xlabel('f');
title('morlet 频域');

数据处理

1.小波系数实部图

2.小波模部等值线图

3.小波方差图
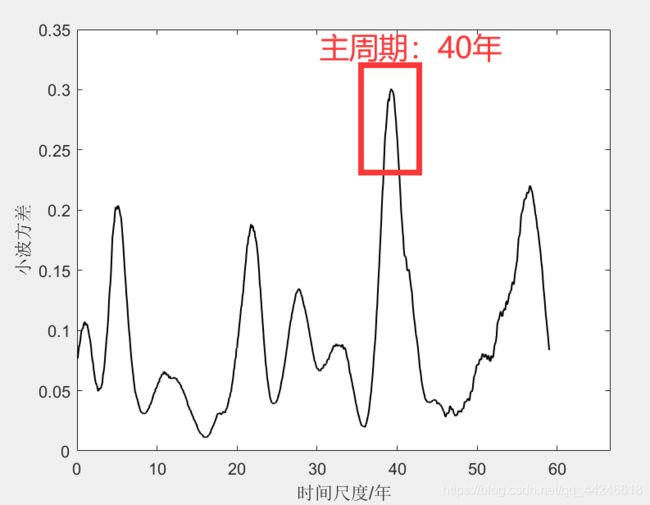
小波方差随尺度a的变化过程，称为小波方差图，它能反映信号波动的能量随尺度a的分布。因此，小波方差图可用来确定信号中不同种尺度扰动的相对强度和存在的主要时间尺度，即主周期。

4.主周期趋势图

根据小波方差检验的结果，绘制演变的第一和第二主周期小波系数图。

具体案例如下：

%进行连续小波变换得到小波系数矩阵,选择复morlet小波函数
    Cab = cwt(Data,1:5:40,'cmor1-1','plot');
    % 求得系数的实部
    realPart=real(Cab);
    
    figure(2)
    contourf(realPart,10,'-');
    colormap('HSV');
    colorbar;
    xlabel('年份');
    ylabel('时间尺度/年');
    set(gca,'XTick',[1:10*12:60*12],'XTickLabel',{'1961','1971','1981','1991','2001','2011'}) %更新XTickLabel

    % 小波方差是模的平方的算数平均
    Module=abs(Cab);
    Module2=Module.^2;
    fangcha=mean(Module2,1);
    figure(3);
    plot(fangcha/12,'k-','linewidth',1);
    xlabel('时间尺度/年');
    ylabel('小波方差');
    set(gca,'XTick',[0:10*12:60*12],'XTickLabel',{'0','10','20','30','40','50','60'}) %更新XTickLabel

得到的相应图像如下所示：

相应小波方差图如下图所示：